Coursera课程自然语言处理(NLP)笔记整理(三)朴素贝叶斯分类器 （第二周课程内容）

1. 贝叶斯公式

1.1. 条件概率

$$P(A|B)=\frac{P(A\cap B)}{P(B)}$$

1.2. 贝叶斯公式

由于
$$P(A|B)=\frac{P(A\cap B)}{P(B)}$$

$$P(B|A)=\frac{P(B\cap A)}{P(A)}$$

则有

$$P(B|A)=P(A|B)\times \frac{P(B)}{P(A)}$$

1.3. 朴素贝叶斯

朴素贝叶斯也是有监督学习的常用模型，与逻辑回归有一定的共同之处
朴素： 这种方法假设用于分类的特征都是独立的。（现实中这种情况很少见）

与之前的类似

I am happy because I am learning NLP
I am happy, not sad
I am sad, I am not learning NLP
I am sad,not happy

可以得到

word	Pos	Neg
I	3	3
am	3	3
happy	2	1
because	1	0
learning	1	1
NLP	1	1
sad	1	2
not	1	2
Nclass	13	13

接下来计算两个class的条件概率

word	Pos	Neg
I	0.24	0.25
am	0.24	0.25
happy	0.15	0.08
because	0.08	0
learning	0.08	0.08
NLP	0.08	0.08
sad	0.08	0.17
not	0.08	0.17
Sum	1	1

概率相等或相近的对感情并无很大影响，大多为中性词，而相差比较大的则对情感有较大影响。

特殊例子是because，它不在Neg组中出现，需要平滑概率函数来解决这个问题

1.3.1. 二值分类的朴素贝叶斯推理条件规则

$${\Sigma }_{i=1}^m\frac{P({\omega }_i|pos)}{P({\omega }_i|neg)}$$

现在假设我们获取了一条新的句子

I am happy today;I am learning

代入公式，则有（我的表和课程不太一样，我没有吧because的概率0提高）

$$\frac{0.24}{0.25}\frac{0.24}{0.25}\frac{0.15}{0.08}\frac{0.24}{0.25}\frac{0.24}{0.25}\frac{0.08}{0.08}$$

其中today不在我们的vocabulary中，因此未作处理。

结果是大于1的，可以猜测是positive

2. 拉普拉斯算子平滑(Laplacian smoothing)

在之前的内容中，我们得知

$$P(w_i|class)=\frac{freq(w_i,class)}{N_{class}},class\in \{pos,neg\}$$

其中N是所有单词的频数。
平滑函数则是

$$P(w_i|class)=\frac{freq(w_i,class)+1}{N_{class}+V_{class}}$$

其中V是class中独立的单词（不重复的）的个数。+1使得0概率得以避免，而分母上的V又使得概率和为1

这个过程就是拉普拉斯平滑。

3. 对数似然

3.1. 似然

word可能有很多种情感，不过在sentiment classification中，它们被分为：neutral，positive和negative三种。（通过他们的条件概率）

$$ratio(w_i)=\frac{P(w_i|Pos)}{P(w_i|Neg)}=\frac{freq(w_i,1)+1}{freq(w_i,0)+1}$$

Neutral的词语的ratio解进1，对负面情绪小于1，正面情绪大于1.

这就称为似然(likelihood)

如果你取positive和negative的比值，这个值称之为先验比例(prior ratio)。
即有
$$\frac{P(pos)}{P(neg)}{\Pi }_{i=1}^m\frac{P(w_i|Pos)}{P(w_i|Neg)}=\frac{freq(w_i,1)+1}{freq(w_i,0)+1}$$

当然如果pos和neg的数量相同则这个先验比例就不存在了。

3.2. 为什么取对数

情感概率的计算需要许多数字和0-1直接的数值相乘，当乘积太小而无法储存在计算机上时便会出现数值下溢(underflow)的风险。
因此我们可以对数值取对数。

$$\log (\frac{P(pos)}{P(neg)}{\Pi }_{i=1}^m\frac{P(w_i|Pos)}{P(w_i|Neg)})=\log (\frac{P(pos)}{P(neg)})+{\Sigma }_{i=1}^m\log (\frac{P(w_i|Pos)}{P(w_i|Neg)})=\log (prior)+\log (likelihood)$$

例：
doc:I am happy because I am learning

$$\lambda (\omega )=\log \frac{P(\omega |pos)}{P(\omega |neg)}$$

表：

word	Pos	Neg	λ
I	0.05	0.05	0
am	0.04	0.04	0
happy	0.09	0.01	2.2
because	0.01	0.01	0
learning	0.03	0.01	1.1
NLP	0.02	0.02	0
sad	0.01	0.09	-2.2
not	0.02	0.03	-0.4

可以计算出

$$\lambda (happy)=\log \frac{0.09}{0.01}\approx 2.2$$

计算Log likelihood

$\log (likelihood)={\Sigma }_{i=1}^m\log \frac{P({\omega }_i|pos)}{P({\omega }_i|neg)}={\Sigma }_{i=1}^m\lambda ({\omega }_i)=3.3$

在对数似然下，只要非中性词才有贡献，比如刚才的句子中只要happy和learning有效，而negative的词语的贡献为负。对数处理下的threshold是0而不是1.

4. 训练朴素贝叶斯分类器

• 1. 收集数据测试模型
• 2. 预处理(与前节相同)
• 3. word计数，计算对应条件概率P(w|pos),P(w|neg)
• 4. 计算λ
• 5. 计算对数先验概率 log(prior) = log(P(pos)/P(neg))

4.1. 观测数据

• 首先依然是引入必要的库

import numpy as np # Library for linear algebra and math utils
import pandas as pd # Dataframe library

import matplotlib.pyplot as plt # Library for plots
from utils import confidence_ellipse # Function to add confidence ellipses to charts

• 为每个tweet计算likelihoods

$$\log (\frac{P(tweet|pos)}{P(tweet|neg)})=\log (P(tweet|pos))-\log (P(tweet|neg))$$

$$positive=\log (P(tweet|pos))={\Sigma }_{i=0}^n\log P(W_i|pos)$$

$$negative=\log (P(tweet|neg))={\Sigma }_{i=0}^n\log P(W_i|neg)$$

此部分代码在assign中，待补充

• 绘制数据
  前两列数据分别是positive和negative

fig, ax = plt.subplots(figsize = (8, 8)) #Create a new figure with a custom size

colors = ['red', 'green'] # Define a color palete

# Color base on sentiment
ax.scatter(data.positive, data.negative, 
    c=[colors[int(k)] for k in data.sentiment], s = 0.1, marker='*')  # Plot a dot for each tweet

# Custom limits for this chart
plt.xlim(-250,0)
plt.ylim(-250,0)

plt.xlabel("Positive") # x-axis label
plt.ylabel("Negative") # y-axis label

可得

可应以看出两个class的word被直线y=x所分开。

• 用置信椭圆(Confidence Ellipses)实现朴素贝叶斯

置信椭圆是一种可视化二维随机变量的方法。比在笛卡尔平面上绘制点的效果梗好。因为在大数据集中，点可能会严重重叠从而隐藏了数据的真实分布。
置信椭圆用四个参数总结数据集的信息:

• 中心:分布的数值平均
• 高度和宽度:和变量的分布相关，用户必须指定绘制椭圆所需的标准偏差量。
• 角度:与属性间的协方差相关。

n_std为正态分布标准差

σ	2σ	3σ
68%	95%	99%

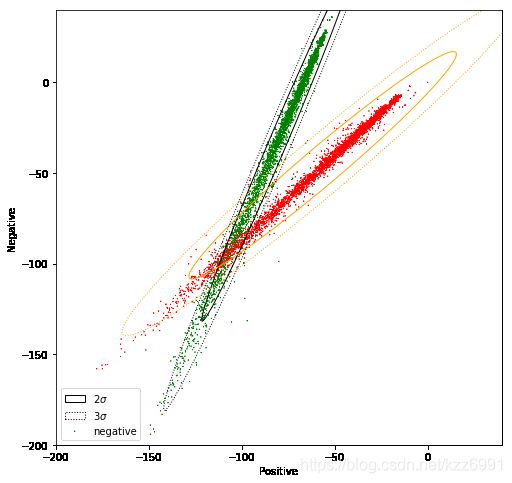
利用函数confidence_ellipse来进行可视化

# Plot the samples using columns 1 and 2 of the matrix
fig, ax = plt.subplots(figsize = (8, 8))

colors = ['red', 'green'] # Define a color palete

# Color base on sentiment

ax.scatter(data.positive, data.negative, c=[colors[int(k)] for k in data.sentiment], s = 0.1, marker='*')  # Plot a dot for tweet

# Custom limits for this chart
plt.xlim(-200,40)  
plt.ylim(-200,40)

plt.xlabel("Positive") # x-axis label
plt.ylabel("Negative") # y-axis label

data_pos = data[data.sentiment == 1] # Filter only the positive samples
data_neg = data[data.sentiment == 0] # Filter only the negative samples

# Print confidence ellipses of 2 std
confidence_ellipse(data_pos.positive, data_pos.negative, ax, n_std=2, edgecolor='black', label=r'$2\sigma$' )
confidence_ellipse(data_neg.positive, data_neg.negative, ax, n_std=2, edgecolor='orange')

# Print confidence ellipses of 3 std
confidence_ellipse(data_pos.positive, data_pos.negative, ax, n_std=3, edgecolor='black', linestyle=':', label=r'$3\sigma$')
confidence_ellipse(data_neg.positive, data_neg.negative, ax, n_std=3, edgecolor='orange', linestyle=':')
ax.legend()

plt.show()

• 修改数据
  两个分布有重叠，使用原始数据的话，朴素贝叶斯方法的精度会比较低。

data2 = data.copy() # Copy the whole data frame

# The following 2 lines only modify the entries in the data frame where sentiment == 1
data2.negative[data.sentiment == 1] =  data2.negative * 1.5 + 50 # Modify the negative attribute
data2.positive[data.sentiment == 1] =  data2.positive / 1.5 - 50 # Modify the positive attribute 

使用同样的方法进行可视化(稍加改动,更换数据集)

data_pos = data2[data2.sentiment == 1] # Filter only the positive samples
data_neg = data[data2.sentiment == 0] # Filter only the negative samples

咋重叠更大了呢

4.2. 使用朴素贝叶斯进行验证

与之前的类似，仍然是用预测函数去进行预测

$$score=predict(X_{val},\lambda ,\log prior)$$

预测结果为score是否大于阈值

$$pred=score>0$$

同样有准确率

$$\frac{1}{m}{\Sigma }_{i=1}^m(pre{d}_i==Y_{va{l}_i})$$

当你使用朴素贝叶斯预测情感时，你实际上做的是通过每个类别中词出现的概率来对其进行估计

实际在的朴素贝叶斯应用包括

• 语义分析
• 作者识别
• 信息检索
• 词义消歧

4.3. 朴素贝叶斯的前提假设

Naive Bayes是一个非常简单的模型，因为它不需要设置任何自定义参数。因为它对数据做出了假设。

• 第一个假设是与每个类相关的预测器或特性之间的独立性。
• 第二个假设与验证集有关。

让我们探讨一下这些假设以及它们如何影响结果。为了说明如何实现特性之间的独立性，让我们看一下下面的句子。

It is sunny and hot in the Sahara Desert

朴素贝叶斯首先假定text中的单词是各个独立的，但是我们可以发现，并非如此，sunny和hot经常同时出现，因此一个句子中的单词并非总是相互独立的，但是朴素贝叶斯就非要这么任务 任性
着可能导致你错误的估计单词的条件概率。

另一个假定和数据集有关，一个好的数据集有相同比例的positive、negative tweets随机样本。
然而，绝大多数的数据集是人工balanced。在实际的tweet流中，positive的tweet比他们的消极反义词出现的更多。（可能是由于negative被禁止货品比等等）这也会影响朴素贝叶斯模型的准确率。

4.4. 错误分析

• punctuation 标点
  例：
  My beloved grandmother

最后的:(是有含义的，却会被处理掉

• removing words 移除单词
  例：
  This is not good,because your attitude is not even cose to being nice
  如果移除像not、this这样的中性词，留下的便是
  Good, attitude, close, nice
  这句话便会被推测为positive，这显然不对。

• word order 词序
  例：

  • I am happy because I did not go
  • I am not happy because I did go
    两句话表现出来截然相反的情感态度，not作为一个重要的节点被朴素贝叶斯分类器忽略了。

• adversarial attack
  对抗性攻击这个术语描述了一些常见的语言现象，比如讽刺、反讽和委婉语。
  人类可以很容易的区分这些，但是机器不能。
  例：

  • This is a ridiculously powerful movie. The plot was gripping and I cried right through until the ending!
    推主很enjoy这个电影
    但是在朴素贝叶斯分类器的视角下
    processed_tweet:[ridicul,power,movi,plot,grip,cry,end]
    情绪就很negative了

5. 代码实现

• 必要的库

from utils import process_tweet, lookup
import pdb
from nltk.corpus import stopwords, twitter_samples
import numpy as np
import pandas as pd
import nltk
import string
from nltk.tokenize import TweetTokenizer
from os import getcwd
# add folder, tmp2, from our local workspace containing pre-downloaded corpora files to nltk's data path
filePath = f"{getcwd()}/../tmp2/"
nltk.data.path.append(filePath)

• 数据集的引入

# get the sets of positive and negative tweets
all_positive_tweets = twitter_samples.strings('positive_tweets.json')
all_negative_tweets = twitter_samples.strings('negative_tweets.json')

# split the data into two pieces, one for training and one for testing (validation set)
test_pos = all_positive_tweets[4000:]
train_pos = all_positive_tweets[:4000]
test_neg = all_negative_tweets[4000:]
train_neg = all_negative_tweets[:4000]

train_x = train_pos + train_neg
test_x = test_pos + test_neg

# avoid assumptions about the length of all_positive_tweets
train_y = np.append(np.ones(len(train_pos)), np.zeros(len(train_neg)))
test_y = np.append(np.ones(len(test_pos)), np.zeros(len(test_neg)))

5.1. 数据的处理

1. 建立dictionary来保存(word,label)对应的频数。
2. 建立lookup()函数来返回元组在tweets出现的次数。

lookup函数有

def lookup(freqs, word, label):
    '''
    Input:
        freqs: a dictionary with the frequency of each pair (or tuple)
        word: the word to look up
        label: the label corresponding to the word
    Output:
        n: the number of times the word with its corresponding label appears.
    '''
    n = 0  # freqs.get((word, label), 0)

    pair = (word, label)
    if (pair in freqs):
        n = freqs[pair]

    return n

count_tweets函数应能实现找出tweets list中每个词在label的情况下出现次数
如: [“i am rather excited”, “you are rather happy”]

有

{ ("rather", 1): 2 ("happi", 1) : 1 ("excit", 1) : 1 }

其实现为

# UNQ_C1 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
def count_tweets(result, tweets, ys):
    '''
    Input:
        result: a dictionary that will be used to map each pair to its frequency
        tweets: a list of tweets
        ys: a list corresponding to the sentiment of each tweet (either 0 or 1)
    Output:
        result: a dictionary mapping each pair to its frequency
    '''

    ### START CODE HERE (REPLACE INSTANCES OF 'None' with your code) ###
    for y, tweet in zip(ys, tweets):
        for word in process_tweet(tweet):
            # define the key, which is the word and label tuple
            pair = (word,y)

            # if the key exists in the dictionary, increment the count
            if pair in result:
                result[pair] += 1

            # else, if the key is new, add it to the dictionary and set the count to 1
            else:
                result[pair] = 1
    ### END CODE HERE ###

    return result

5.2. 训练朴素贝叶斯模型

建立好字典

# Build the freqs dictionary for later uses

freqs = count_tweets({}, train_x, train_y)

• 计算unique words的数量V
• 计算每个单词的pos频率freq_pos和neg频率freq_neg
• 计算pos单词总数N_pos,neg单词总数N_neg以及unique pos单词总数V_pos，unique neg单词总数V_neg
• 计算条目总数D，pos条目总数D_pos,neg条目总数D_neg
• 计算log prior
• 计算对数似然 log likelihood(使用拉普拉斯算子平滑)

代码实现

# UNQ_C2 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
def train_naive_bayes(freqs, train_x, train_y):
    '''
    Input:
        freqs: dictionary from (word, label) to how often the word appears
        train_x: a list of tweets
        train_y: a list of labels correponding to the tweets (0,1)
    Output:
        logprior: the log prior. (equation 3 above)
        loglikelihood: the log likelihood of you Naive bayes equation. (equation 6 above)
    '''
    loglikelihood = {}
    logprior = 0

    ### START CODE HERE (REPLACE INSTANCES OF 'None' with your code) ###

    # calculate V, the number of unique words in the vocabulary
    vocab = set([pair[0] for pair in freqs.keys()])
    V = len(vocab)

    # calculate N_pos, N_neg, V_pos, V_neg
    N_pos = N_neg = V_pos = V_neg = 0
    for pair in freqs.keys():
        # if the label is positive (greater than zero)
        if pair[1] > 0:
            # increment the count of unique positive words by 1
            V_pos += 1

            # Increment the number of positive words by the count for this (word, label) pair
            N_pos += freqs[pair]

        # else, the label is negative
        else:
            # increment the count of unique negative words by 1
            V_neg += 1

            # increment the number of negative words by the count for this (word,label) pair
            N_neg += freqs[pair]

    # Calculate D, the number of documents
    D = len(train_y)

    # Calculate D_pos, the number of positive documents
    D_pos = sum(train_y)

    # Calculate D_neg, the number of negative documents
    D_neg = D-D_pos

    # Calculate logprior
    logprior = np.log(D_pos/D_neg)

    # For each word in the vocabulary...
    for word in vocab:
        # get the positive and negative frequency of the word
        if (word,1) in freqs.keys():
            freq_pos = freqs[(word,1)]
        else:
            freq_pos = 0
        if (word,0) in freqs.keys():
            freq_neg = freqs[(word,0)]
        else:
            freq_neg = 0
        # calculate the probability that each word is positive, and negative
        p_w_pos = (freq_pos+1)/(N_pos+V)
        p_w_neg = (freq_neg+1)/(N_neg+V)

        # calculate the log likelihood of the word
        loglikelihood[word] = np.log(p_w_pos/p_w_neg)

    ### END CODE HERE ###

    return logprior, loglikelihood

5.3. 测试贝叶斯模型

5.3.1. 进行预测

预测概率有

$$p=\log prior+{\Sigma }_i^N(loglikelihoo{d}_i)$$

对应实现有

# UNQ_C4 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
def naive_bayes_predict(tweet, logprior, loglikelihood):
    '''
    Input:
        tweet: a string
        logprior: a number
        loglikelihood: a dictionary of words mapping to numbers
    Output:
        p: the sum of all the logliklihoods of each word in the tweet (if found in the dictionary) + logprior (a number)

    '''
    ### START CODE HERE (REPLACE INSTANCES OF 'None' with your code) ###
    # process the tweet to get a list of words
    word_l = process_tweet(tweet)

    # initialize probability to zero
    p = 0

    # add the logprior
    p += logprior
    
    for word in word_l:

        # check if the word exists in the loglikelihood dictionary
        if word in loglikelihood:
            # add the log likelihood of that word to the probability
            p += loglikelihood[word]

    ### END CODE HERE ###

    return p

5.3.2. 进行测试

# UNQ_C6 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
def test_naive_bayes(test_x, test_y, logprior, loglikelihood):
    """
    Input:
        test_x: A list of tweets
        test_y: the corresponding labels for the list of tweets
        logprior: the logprior
        loglikelihood: a dictionary with the loglikelihoods for each word
    Output:
        accuracy: (# of tweets classified correctly)/(total # of tweets)
    """
    accuracy = 0  # return this properly

    ### START CODE HERE (REPLACE INSTANCES OF 'None' with your code) ###
    y_hats = []
    for tweet in test_x:
        # if the prediction is > 0
        if naive_bayes_predict(tweet, logprior, loglikelihood) > 0:
            # the predicted class is 1
            y_hat_i = 1
        else:
            # otherwise the predicted class is 0
            y_hat_i = 0

        # append the predicted class to the list y_hats
        y_hats.append(y_hat_i)

    # error is the average of the absolute values of the differences between y_hats and test_y

    error = np.mean((np.array(y_hats).transpose() != np.array(test_y)))

    # Accuracy is 1 minus the error
    accuracy = 1 - error#为啥不直接算呢

    ### END CODE HERE ###

    return accuracy

5.3.3. 用实例测试

# UNQ_C7 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
# You do not have to input any code in this cell, but it is relevant to grading, so please do not change anything

# Run this cell to test your function
for tweet in ['I am happy', 'I am bad', 'this movie should have been great.', 'great', 'great great', 'great great great', 'great great great great']:
    # print( '%s -> %f' % (tweet, naive_bayes_predict(tweet, logprior, loglikelihood)))
    p = naive_bayes_predict(tweet, logprior, loglikelihood)
#     print(f'{tweet} -> {p:.2f} ({p_category})')
    print(f'{tweet} -> {p:.2f}')

有结果

I am happy -> 2.15
I am bad -> -1.29
this movie should have been great. -> 2.14
great -> 2.14
great great -> 4.28
great great great -> 6.41
great great great great -> 8.55

5.3.4. 通过积极消极ratio过滤词语

5.3.4.1. 获取ratio

$$ratio=\frac{po{s}_{w}ords+1}{ne{g}_{w}ords+1}$$

对应代码有

# UNQ_C8 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
def get_ratio(freqs, word):
    '''
    Input:
        freqs: dictionary containing the words
        word: string to lookup

    Output: a dictionary with keys 'positive', 'negative', and 'ratio'.
        Example: {'positive': 10, 'negative': 20, 'ratio': 0.5}
    '''
    pos_neg_ratio = {'positive': 0, 'negative': 0, 'ratio': 0.0}
    ### START CODE HERE (REPLACE INSTANCES OF 'None' with your code) ###
    # use lookup() to find positive counts for the word (denoted by the integer 1)
    pos_neg_ratio['positive'] = lookup(freqs,word,1)

    # use lookup() to find negative counts for the word (denoted by integer 0)
    pos_neg_ratio['negative'] = lookup(freqs,word,0)

    # calculate the ratio of positive to negative counts for the word
    pos_neg_ratio['ratio'] = (pos_neg_ratio['positive'] +1)/(pos_neg_ratio['negative']+1)
    ### END CODE HERE ###
    return pos_neg_ratio

5.3.4.2. 根据阈值获取词语

# UNQ_C9 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
def get_words_by_threshold(freqs, label, threshold):
    '''
    Input:
        freqs: dictionary of words
        label: 1 for positive, 0 for negative
        threshold: ratio that will be used as the cutoff for including a word in the returned dictionary
    Output:
        word_set: dictionary containing the word and information on its positive count, negative count, and ratio of positive to negative counts.
        example of a key value pair:
        {'happi':
            {'positive': 10, 'negative': 20, 'ratio': 0.5}
        }
    '''
    word_list = {}

    ### START CODE HERE (REPLACE INSTANCES OF 'None' with your code) ###
    for key in freqs.keys():
        word, _ = key

        # get the positive/negative ratio for a word
        pos_neg_ratio = get_ratio(freqs,word)

        # if the label is 1 and the ratio is greater than or equal to the threshold...
        if label == 1 and pos_neg_ratio["ratio"] >= threshold:

            # Add the pos_neg_ratio to the dictionary
            word_list[word] = pos_neg_ratio

        # If the label is 0 and the pos_neg_ratio is less than or equal to the threshold...
        elif label == 0 and pos_neg_ratio["ratio"] <= threshold:

            # Add the pos_neg_ratio to the dictionary
            word_list[word] = pos_neg_ratio

        # otherwise, do not include this word in the list (do nothing)

    ### END CODE HERE ###
    return word_list

5.3.4.3. 错误分析

print('Truth Predicted Tweet')
for x, y in zip(test_x, test_y):
    y_hat = naive_bayes_predict(x, logprior, loglikelihood)
    if y != (np.sign(y_hat) > 0):
        print('%d\t%0.2f\t%s' % (y, np.sign(y_hat) > 0, ' '.join(
            process_tweet(x)).encode('ascii', 'ignore')))

6. 完整程序

完整程序
完整程序