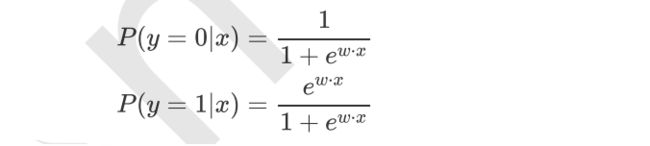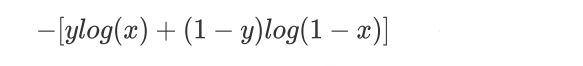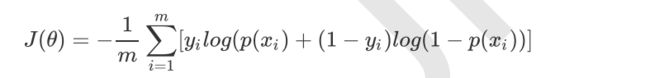机器学习-P6 逻辑回归（书P73）

一，概述

分类计数是机器学习和数据挖掘应用中的重要组成部分。在数据科学中，大约70%的问题属于分类问题。解决分类问题的算法也有很多种，比如：

• k - 近邻算法：使用距离计算来实现分类
• 决策树：通过构建直观易懂得树来实现分类
• 朴素贝叶斯：使用概率论构建分类器
• 逻辑回归：用来解决二分类问题的回归方法，它主要是通过寻找最优参数来正确的分类原始数据。

1，逻辑回归（Logistic Regression）

逻辑回归（简称：LR），其实是一个很有误导性的概念，虽然名字上有回归两个字，但是他最擅长的是处理分类问题
LR分类器适用于各项广义上的分类问题，例如：

• 评论信息的正负情感分析（二分类）
• 用户点击率（二分类）
• 用户违约信息预测（二分类）
• 垃圾邮件检测（二分类）
• 疾病预测（二分类）
• 用户等级分类（二分类）…

我们主要讨论的是二分类问题。

1.1，线性回归

传送门：线性回归的实现
传送门：sklearn 中的线性回归使用

逻辑回归与线性回归同属于广义线性回归模型，逻辑回归就是用线性回归模型的预测值去拟合真是标签的对数几率（一个事件的几率（odds）是指该事件发生的概率与不发生的概率之比，例如：发生概率为P，则几率为 P/(1-P)，对数几率就是 log(P/(1-P)) ）。

逻辑回归与线性回归本质上都是得到一条直线，不同的是，线性回归的直线是尽可能取拟合输入变量x的分布，使得训练集中所有样本点到直线的距离最短；而逻辑回归的直线是尽可能地去拟合决策边界，使得训练集样本中的样本点尽可能分类开。因此，两者的目的是不同的。

线性回归方程：

• y = wx + b

此处，y 为因变量，x 为自变量。
机器学习中，y 为标签，x 为特征。

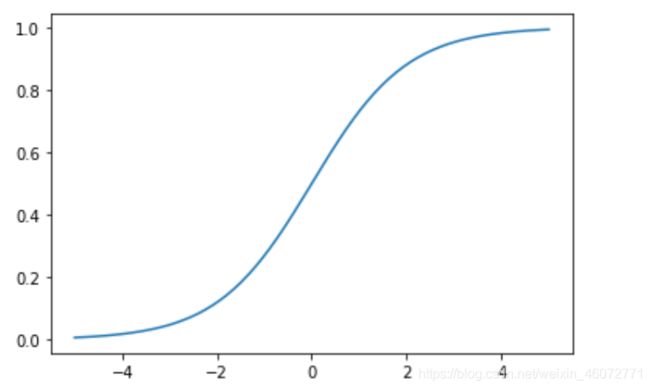
1.2，Sigmoid函数

我们想要的函数应该是，能接受所有的输入然后预测出类别。例如在二分类情况下，函数能输出0或1。那拥有这类性质的函数称为海维赛德阶跃函数（Heaviside step function），又称之为单位阶跃函数（如下图所示）

单位阶跃函数的问题在于：在0点位置该函数从0瞬间跳跃到1，在这个瞬间跳跃过程中很难处理（不好求导）。幸运的是，Sigmoid函数也有类似的性质，且数学上更容易处理。

Sigmoid函数公式：

• f(x) = 1 / ( 1 + e^-(x) )

import numpy as np
import math
import matplotlib.pyplot as plt
%matplotlib inline

x = np.linspace(-5, 5, 200) # 从[-5, 5]中等间距找出 200 个数
y = [1/(1 + math.e**(-i) ) for i in x]
plt.plot(x, y)
plt.show()

放大横坐标看一下 ↓

x = np.linspace(-60, 60, 200)
y = [1/(1 + math.e**(-i) ) for i in x]
plt.plot(x, y)
plt.show()

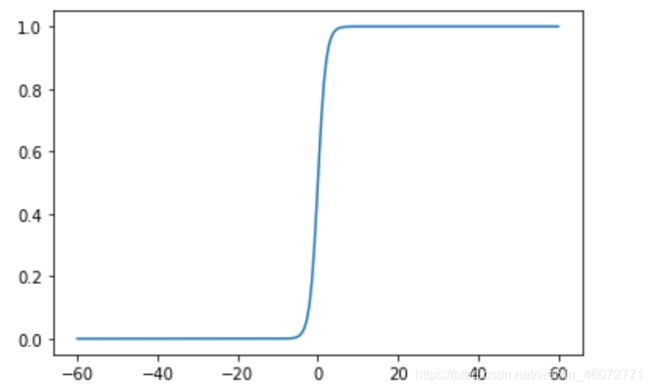
上边给出了Sigmoid函数在不同坐标尺度下的两条曲线。当x = 0时，Sigmoid函数值为0.5。随着x的增多，对应的函数值将逼近与1；而随着x的减小，函数值逼近与0。所以Sigmoid函数值域为（0,1），注意这是开区间，仅仅接近0和1。若果横纵坐标刻度足够大，Sigmoid函数看起来很像一个阶跃函数。

1.3，逻辑回归

通过线性回归和Sigmoid函数结合，我们可以得到逻辑回归的公式：

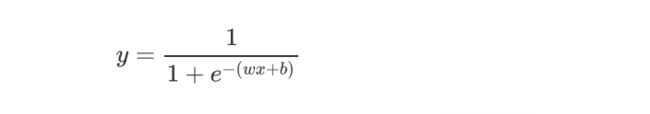
这样 y ∈（0,1）。
对式子进行变换，可得：

这其实就是个对数几率公式

• 二项Logistic回归：
  
• 多项Logistic回归：
  

1.4，LR与线性回归的区别

逻辑回归与线性回归是两类模型

• 逻辑回归是分类模型
• 线性回归是回归模型

2，LR的损失函数

损失函数可以用来衡量模型预测的好坏。
损失函数，通俗讲，就是衡量真实值和预测值之间的差距的函数。
所以，损失函数越小，模型就越好。
在这里，最小损失是0。

• LR损失函数为：
  
  看一下损失函数的图像 ↓

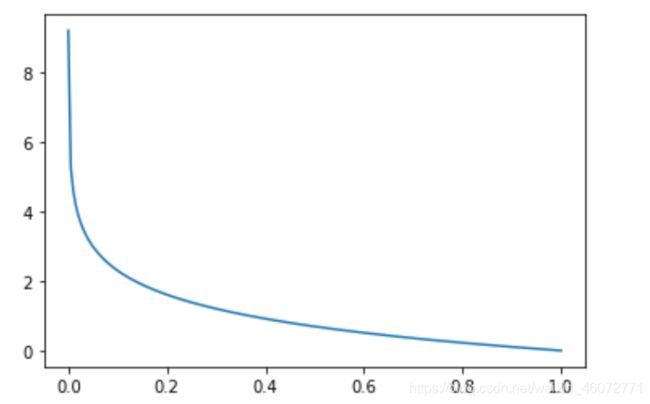
x = np.linspace(0.0001, 1, 200)
y = [(-np.log(i)) for i in x]
plt.plot(x, y)
plt.show()

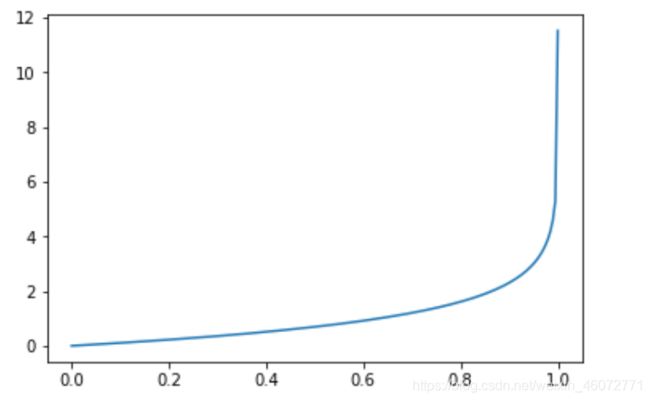
x = np.linspace(0, 0.99999, 200)
y = [(-np.log(1 - i)) for i in x]
plt.plot(x, y)
plt.show()

• 我们把这两个损失函数综合起来看：
  
  y就是标签，分别去0,1。
• 对于m个样本，总的损失函数为：
  
• m是样本数
• y是标签，取值0或1
• i 表示第 i 个样本
• p(x)表示预测的输出

不过当损失过于小的时候，也就是模型能够拟合绝大部分的数据，这时候就容易出现过拟合。为了防止过拟合，我们会引入正则化。

3，LR 正则化

3.1，L1正则化

Lasso回归，相当于为模型添加了这样一个先验条件：w服从零均值拉普拉斯分布。

• 拉普拉斯分布：
  
  （其中u，b为常数，且u > 0）

下面证明这一点，由于引入了先验条件，所以似然函数如下：

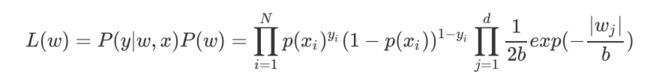
再log 再取负，得到目标函数：

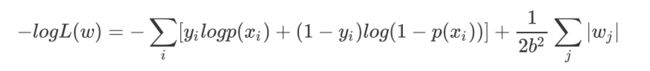
等价于原始的cross-entropy后面加上L1正则，因此L1正则的本质其实是为模型增加了“模型参数服从零均值拉普拉斯分布”这一先验条件。

3.2，L2正则化（岭回归）

Ridge回归，相当于为模型添加了这样一个先验条件：w服从零均值正态分布。

• 正态分布公式：
  
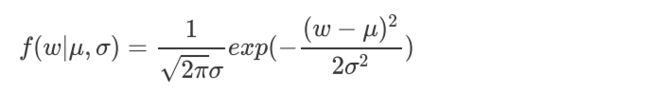
  下面证明这一点，由于引入了先验条件，所以似然函数如下：
  
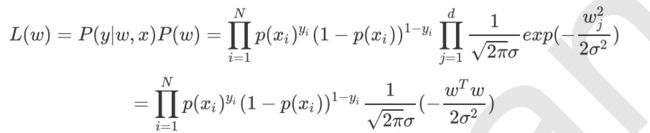
  再log 再取负，得到目标函数：
  
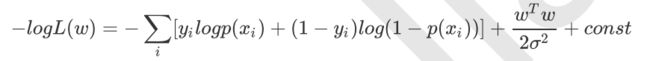
  等价于原始的cross-entropy后面加上L2正则，因此L2正则的本质其实是为模型增加了“模型参数服从零均值正态分布”这一先验条件。

3.3，L1正则化与L2正则化的区别

1，关系模型参数的先验知识不同

• L1是拉普拉斯分布
• L2是正态分布

2，L1偏向于是模型变得稀疏（但实际上并不容易），L2偏向于是模型每个参数都很小，但是更加稠密，从而防止过拟合。

为什么L1偏向于稀疏，L2偏向于稠密？
看下边两张图，每个圆表示loss的等高线，即在该圆上loss都是相等的，可以看到L1更容易在坐标轴上达到，而L2更容易在象限中达到。

4，RL损失函数求解

4.1，基于对数似然损失函数

对数似然损失函数：

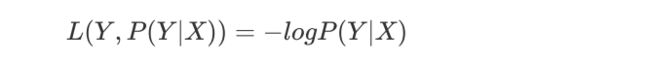
对于LR来说，单个样本的对数似然损失函数可以写成如下形式：

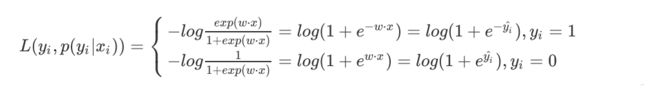
综合起来，写成同一个式子：

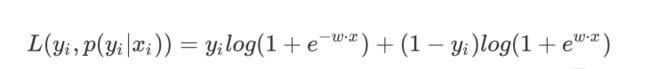
于是对整个训练集样本而言，对数似然损失函数是：

4.2，基于极大似然估计

假设样本是独立同分布生成的，他们的似然函数就是个样本后验概率连乘：

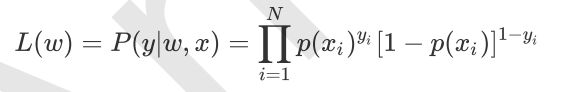
为了防止数据下溢，写成对数似然函数形式：

讨论：损失函数为什么是log损失函数（交叉熵），而不是MSE?
假设目标函数是MSE，即：

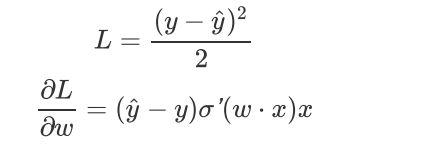
这里Sigmoid的导数项：

根据w的初始化，到数值可能很小（想象一下Sigmoid函数在输入较大时的梯度）而导致收敛变慢，而训练途中也可能因为该值过小而提早终止训练。

另一方面，Logless的梯度如下，当模型输入概率偏离于真实概率时，梯度较大，加快训练速度，当过拟合值接近于真是概率时训练速度变缓慢，没有MSE的问题。

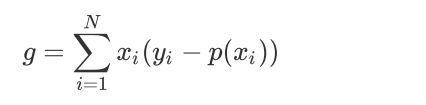
二，梯度下降法

由于极大似然函数无法直接求解，所以在机器学习算法中，在最小化损失函数时，可以通过梯度下降法来一步步的迭代求解，得到最小化的损失函数和模型参数值。

1，梯度

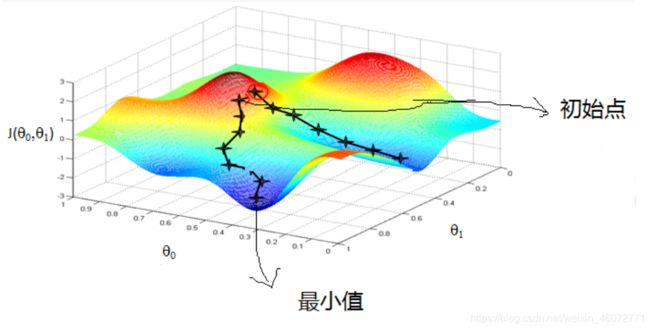
2，梯度下降的直观解释

3，梯度下降的详细算法

梯度下降的算法可以有代数法和矩阵法（也称向量法）两种表示；

• 代数法
  如果对矩阵分析不熟悉，则代数法更加容易理解。
• 矩阵法（向量法）
  矩阵法更加简介，且由于使用了矩阵，实现逻辑更加一目了然。

3.1，梯度下降的代数方式描述

1，先决条件：确认优化模型的假设函数和损失函数。


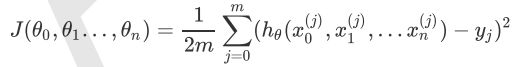
2，算法相关参数初始化：主要是初始化θ1,θ2, … ,θn，算法终止距离ε以及常α。在没有任何先验知识的时候，我们比较倾向于将所有的θ初始化为0，将步长初始化为1。在调优的时候在进行优化。

3，算法过程
（1）确定当前位置的损失函数梯度，对于θi，其梯度表达式如下：
（2）用步长乘以损失函数的梯度，得到当前位置的下降距离，即
，对应于前边登山例子中的某一步。

（3）确定是否所有θi，梯度下降的距离都小于ε，如果小于ε则算法终止，当前所有的θi(i = 0,1, … ,n)即为最终结果。否则进入步骤（4）；

（4）更新所有的θ，对于θi，其更新表达式如下。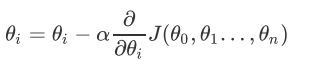更新完毕后继续转入步骤（1）。

举个例子
下边用线性回归的例子来具体描述梯度下降。假设我们的样本是
则算法过程步骤（1）中对于θi的偏导数计算如下：

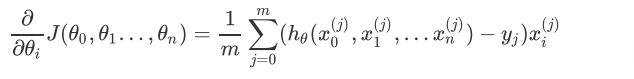
由于样本中没有x0上式中另所有的x0^j为1，步骤（4）中的θi的更新表达式如下：

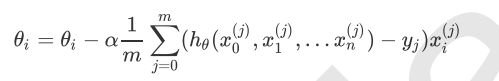
从这个例子可以看出当前点的梯度方向是由所有的样本决定的，加1/m是为了好理解，由于步长也是常数，他们的乘积也为常数，所以这里α(1/m)可以用一个常数表示。

3.2，梯度下降法的矩阵方式描述

与代数方式相比，矩阵法要求有一定的矩阵分析的基础知识，尤其是矩阵求导。

1，先决条件：需要确认优化模型的假设函数和损失函数。对于线性回归，假设函数的矩阵表达方式为：

2，算法相关参数初始化：θ向量可以初始化为默认值，或者调优后的数值。算法终止距离ε，步长α和3.1比没有变化。

3，算法过程
（1）确定当前位置的损失函数的梯度，对于θ向量，其梯度表示如下：



还是用线性回归的例子来描述具体的算法过程。损失函数对于θ向量的偏导数如下：

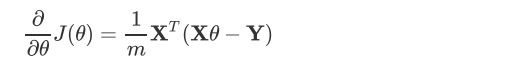
在步骤（4）中θ向量的更新表达式如下：

可以看出简洁了很多。
这里用到了矩阵求导链式法则，和两个矩阵求导公式。

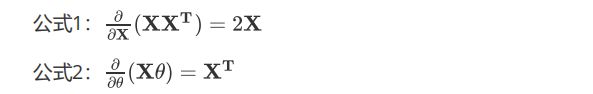
4，梯度下降的种类

4.1，批量梯度下降法（BGD）

最常用的形式，具体做法也是在更新参数时使用所有样本来进行更新。

由于我们有m个样本，这里求梯度时就用了所有的样本的梯度数据。

• 会获得全局最优解
• 计算量大，速度慢

4.2，随机梯度下降法（SGD）

与BGD原理类似，区别在于没有用所有的m个样本的数据，而仅仅取了一个样本j来求梯度。对于更新公式如下：

• 训练速度快
• 解很有可能不是最优的
• 由于随机梯度下降法一次迭代一个样本，导致迭代方向变化很大，不能很快的收敛到局部最优解。
• SGD很适合处理非凸函数优化，由于下降方法具有一定的随机性，因此能很好地绕开局部最优解，从而逼近全局最优解。

4.3，小批量梯度下降法（MBGD）

是批量和梯度的一种折中，也就是对于m个样本，我们采用x个子样本来迭代，1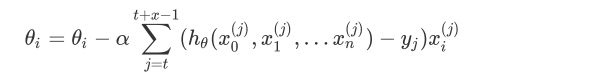

• 结合了BGD和SGD的优点
• 可以的得到更急稳定的收敛结果

5，梯度下降的算法调优

1，选择合适的步长：可以多去一些值，从大到小，分别运行算法，看看迭代效果，若果损失函数在变小，说明取值有效，否则增大步长。

• 太大：导致迭代过快，甚至有可能错过最优解。
• 太小：迭代速度慢，很长时间算法都不能结束。

2，算法参数的初始值：初始值不同，获得的最小值也有可能不同，因此梯度下降求得的知识局部最小值；当然如果算是函数是凸函数则一定是最优解。由于有局部最优解的风险，需要多次用不同初始值运行算法，关键损失函数的最小值，选择损失函数最小的初值。

3，标准化：由于样本特征的取值范围不同，可能导致迭代很慢，为了减少特征取值的影响，可以对特征数据标准化，也就是进行如下计算：（std 标准差）

这样特征的新期望为0，新方差为1，收敛速度可以大大加快。

三，使用梯度下降求解逻辑回归

testSet数据集中共有100个点，每个点包括两个数值特征：X1和X2。因此可以将数据在一个二维平面上展示出来。我们可以将第一列数据（X1）看做x轴上的值，将第二列数据（X2）看做y轴上的值。而最后一列数据即为分类标签。
跟标签的不同，对这些点进行分类。
在次数据集上，我们将通过批量梯度下降法和随机梯度下降法找出最佳回归系数。

1，使用BGD求解逻辑回归

BGD：批量梯度下降法
批量梯度下降法伪代码：

为个回归系数初始化为1
重复下面步骤直至收敛：
→→计算整个数据集梯度
→→使用α * gradient更新回归系数的向量
返回回归系数

1.1，导入数据集

import pandas as pd
import numpy as np

dataSet = pd.read_table('D:/Python/pycharm/机器学习/逻辑回归/testSet.txt',header=None)
dataSet.columns = ['x1','x2','labels']
dataSet

1.2，定义辅助函数

Sigmoid函数

"""
函数功能：计算Sigmoid函数
参数说明：
    inX：数值型数据
返回：
    s：经过Sigmoid函数计算后的函数值
"""
def sigmoid(inX):
    s = 1/(1 + np.exp(-inX))
    return s

标准化函数（数据归一化）

"""
函数功能：标准化（期望值为0，方差为1）
参数说明：
    xMat：特征矩阵
返回：
    inMat：标准化之后的特征矩阵
"""
def regularize(xMat):
    inMat = xMat.copy()
    inMeans = np.mean(inMat, axis=0)
    inVar = np.std(inMat, axis=0)
    inMat = (inMat - inMeans)/inVar
    return inMat

1.3，BGD算法python实现

"""
函数功能：使用BGD求解逻辑回归
参数说明：
    dataSet：DF数据集
    alpha：步长
    maxCycles：最大迭代次数
返回：
    weights：各特征权重值
"""
def BDG_LR(dataSet, alpha=0.001,maxCycles=500):
    xMat = np.mat(dataSet.iloc[:,:-1].values)
    yMat = np.mat(dataSet.iloc[:,-1].values).T
    xMat = regularize(xMat)
    m, n = xMat.shape
    weights = np.zeros((n, 1))
    for i in range(maxCycles):
        grad = xMat.T * (xMat * weights - yMat)/m
        weights = weights - alpha * grad
    return weights

BDG_LR(dataSet, alpha=0.001,maxCycles=500)
>>>matrix([[ 0.00216921],
           [-0.16320532]])

可以看出来，第二个属性更加重要（权重较高）

传送门：Python中flatten( ),matrix.A用法

• flatten()：扁平化
• matrix.A：由 matrix → array

# 生成权重矩阵
ws = BDG_LR(dataSet)
# 属性 - 标签
xMat = np.mat(dataSet.iloc[:,:-1].values)
yMat = np.mat(dataSet.iloc[:,-1].values).T
# 对属性进行归一化
xMat = regularize(xMat)
# 将矩阵扁平化
(xMat * ws).A.flatten()
>>>array([-2.64123468e-01,  6.49184006e-02, -1.33158642e-04, -2.28858688e-02,
       -1.57419535e-01, -1.66449862e-02, -2.16530275e-01, -1.49041037e-02,
       -1.03968632e-01, -1.36118789e-01, -1.06273270e-02, -2.30591543e-01,
        1.22521981e-01, -9.24294354e-02,  2.80963501e-02,  1.77772270e-01,
        1.48819104e-02,  1.37072059e-01,  2.16115466e-01,  3.08510560e-02,
        1.21782170e-01,  2.48701086e-01, -1.84857524e-01,  2.90802395e-01,
        1.33836305e-01, -1.04464790e-01, -9.05032154e-02,  2.82522520e-01,
        1.08313978e-01, -1.04879201e-01,  9.05733263e-02, -5.97173032e-02,
       -1.74737188e-01,  3.14621708e-01,  5.95308542e-02, -1.04336279e-01,
       -9.65156791e-02, -1.08334128e-01, -1.99754139e-01, -1.69408277e-01,
        1.14898853e-01,  1.85164766e-02, -1.33451948e-01,  2.14945252e-01,
        1.39211067e-01, -1.42657986e-01,  3.07386529e-01,  2.34723999e-02,
       -1.77676134e-01, -1.55123412e-01, -7.54713409e-02, -1.33138102e-01,
       -5.31411965e-02, -2.51157832e-01,  5.74252584e-02, -9.04208502e-03,
       -1.46941707e-01, -3.70755298e-02, -1.77771965e-01,  6.38470360e-02,
        8.51414551e-02,  1.63847995e-01, -8.83409389e-02, -2.06742599e-01,
       -2.00881065e-01,  2.82426490e-01,  8.16541319e-03, -1.75316690e-01,
       -1.92118526e-01, -1.58079904e-01, -1.56973191e-01,  2.13137205e-01,
       -2.54062040e-01,  1.30372921e-01, -1.16009408e-01, -3.33282316e-02,
        2.30040938e-01,  1.57953156e-01,  5.87262809e-02,  7.60613574e-02,
        1.52862541e-02,  3.42524088e-01, -1.27600415e-01, -5.89181623e-02,
        1.70500845e-01,  2.91840351e-01,  9.46671306e-02, -2.11186597e-01,
        4.23343252e-02,  2.30204083e-01,  2.57593225e-01, -2.12690159e-01,
       -1.11578786e-01,  1.99832444e-01,  1.87800113e-01,  1.43146264e-01,
       -1.44048412e-01,  2.23055024e-01, -9.51413285e-02, -2.87723528e-01])

来看一下错误率吧~

p = sigmoid(xMat * ws).A.flatten()
for i, j in enumerate(p):
    if j < 0.5:
        p[i] = 0
    else:
        p[i] = 1

train_error = (np.fabs(yMat.A.flatten() - p)).sum()
train_error_rate = train_error / yMat.shape[0]
train_error_rate
>>>0.08  

1.4，准确率计算函数

将上述过程封装为函数（注意上边计算的是错误率，下边的是准确率！）

"""
函数功能：计算准确率
参数说明：
    dataSet：DF数据集
    method：计算权重函数
    alpha：步长
    maxCycles：最大迭代次数
返回：
    trainAcc：模型预测准确率
"""
def logisticAcc(dataSet, method, alpha=0.01, maxCycles=500):
    weights = method(dataSet, alpha=alpha, maxCycles=maxCycles)
    p = sigmoid(xMat * ws).A.flatten()
    for i,j in enumerate(p):
        if j < 0.5:
            p[i] = 0
        else:
            p[i] = 1
    train_error = (np.fabs(yMat.A.flatten() - p)).sum()
    trainAcc = 1 - train_error / yMat.shape[0]
    return trainAcc

logisticAcc(dataSet, method)
>>>0.92

2，使用SGD求解逻辑回归

SGD：随机梯度下降法
伪代码如下：

为个回归系数初始化为1
对数据集中每个样本：
→→计算该样本梯度
→→使用α * gradient更新回归系数的向量
返回回归系数

2.1，SGD算法的python实现

传送门：Python：sample函数

"""
函数功能：使用SGD求解逻辑回归
参数说明：
    dataSet：DF数据集
    alpha：步长
    maxCycles：最大迭代次数
返回：
    weights：各特征权重值
"""
def SGD_LR(dataSet, alpha=0.001,maxCycles=500):
    dataSet = dataSet.sample(maxCycles, replace=True)
    dataSet.index = range(dataSet.shape[0])
    
    xMat = np.mat(dataSet.iloc[:,:-1].values)
    yMat = np.mat(dataSet.iloc[:,-1].values).T
    xMat = regularize(xMat)
    m, n = xMat.shape
    weights = np.zeros((n, 1))
    for i in range(m):
        grad = xMat[i].T * (xMat[i] * weights - yMat[i])
        weights = weights - alpha * grad
    return weights

SGD_LR(dataSet)
>>>matrix([[ 0.0162472 ],
           [-0.16570291]])

2.2，计算准确率

logisticAcc(dataSet, SGD_LR)
>>>0.92

四，从疝气病症预测病马的死亡率

数据中有30%的值是缺失的。
下边会先介绍如何处理数据缺失问题，然后再利用逻辑回归进行预测。

1，准备数据

数据中的缺失值是一个非常棘手的问题，很多文献致力于解决这个问题。那么，数据缺失会带来什么问题呢？假设100个样本和20个特征，这些数据都是机器收集回来的。若机器上的某个传感器损坏导致一个特征无效时该怎么办呢？他们是否还可用？答案是肯定的。因为有时候数据相当昂贵，舍弃和重新获取都是不可取的，所以必须采用一些办法来解决这个问题。下边给出可选的做法：

• 使用可用特征均值来填补缺失值
• 使用特殊值来填补缺失值，如：-1
• 忽略缺失值得样本
• 使用相似样本的均值补缺失值
• 使用另外的机器学习算法来预测缺失值

预处理数据做两件事：

• 如果测试集中一条数据的特征值已经缺失，那么我们选择实数0来替换所有缺失值，因为本文使用逻辑回归。因此这样做不会影响回归系数的值。Sigmoid(0) = 0.5，即他对结果的预测不具有任何倾向性。
• 如果测试集中一条数据的类别标签已经缺失，那么将该类别数据丢弃，因为类别数据与特征不同，很难确定采用某个合适的值来替换。

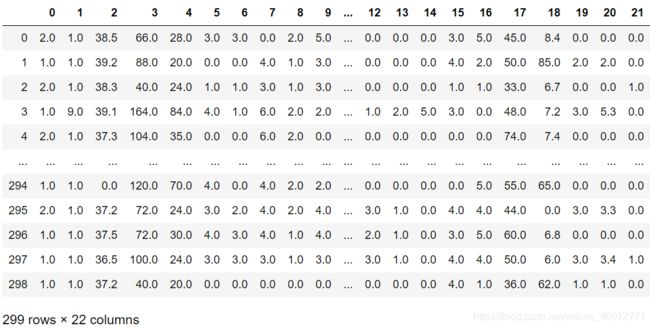
处理后的数据集如下：

train = pd.read_table('D:/Python/pycharm/机器学习/逻辑回归/horseColicTraining.txt',header=None)
test = pd.read_table('D:/Python/pycharm/机器学习/逻辑回归/horseColicTest.txt',header=None)
train

train.info()
>>><class 'pandas.core.frame.DataFrame'>
	RangeIndex: 299 entries, 0 to 298
	Data columns (total 22 columns):
	0     299 non-null float64
	1     299 non-null float64
	2     299 non-null float64
	3     299 non-null float64
	4     299 non-null float64
	5     299 non-null float64
	6     299 non-null float64
	7     299 non-null float64
	8     299 non-null float64
	9     299 non-null float64
	10    299 non-null float64
	11    299 non-null float64
	12    299 non-null float64
	13    299 non-null float64
	14    299 non-null float64
	15    299 non-null float64
	16    299 non-null float64
	17    299 non-null float64
	18    299 non-null float64
	19    299 non-null float64
	20    299 non-null float64
	21    299 non-null float64
	dtypes: float64(22)
	memory usage: 51.5 KB

2，逻辑回归分类函数

得到训练集和测试集之后，我们可以利用前边的BGD_LR或者SGD_LR得到训练集weights。
这里需要定义一个分类函数，根据Sigmoid函数返回的值来确定y是0还是1

"""
函数功能：给定测试数据集和权重，返回标签类别
参数说明：
    inX：测试函数
    weights：特征权重
"""
def classify(inX,weights):
    p = sigmoid(sum(inX * weights))
    if p < 0.5:
        return 0
    else:
        return 1 

构建Logistic模型：

"""
函数功能：logistic分类模型
参数说明：
    train：测试集
    test：训练集
    alpha：步长
    maxCycles：最大迭代次数
返回：
    retest：预测号标签的测试集
"""
def get_acc(train, test, alpha=0.001, maxCycles=5000):
    weights = SGD_LR(train, alpha=alpha, maxCycles=maxCycles)
    xMat = np.mat(test.iloc[:,:-1].values)
    xMat = regularize(xMat)
    result = []
    for inX in xMat:
        label = classify(inX, weights)
        result.append(label)
    retest = test.copy()
    retest['predict'] = result
    acc = (retest.iloc[:,-1] == retest.iloc[:,-2]).mean()
    print(f'模型准确率为：{acc}')
    return retest

get_acc(train, test)
>>>模型准确率为：0.746268656716418

（2020年4月7日17:38:55）