第十一届蓝桥杯省赛第二场 Python组

引言

博主没有参加第十一届蓝桥杯，这是在官网上找到的历年真题，按年份倒序刷吧。

我会以Python语言的角度去分析题目的考点。

试题A：门牌制作

本题考察的点是Python字符串处理函数中的count()函数，具体用处是统计字符串中出现子串的次数。

我们把题目要求的 2 当作子串，统计从 1 到 2020 这些字符串中出现子串 2 的次数即可。

res = 0
for num in range(1, 2021):
    res += str(num).count('2')
print(res)
# 输出624

另外，我觉得值得注意的是，虽然本题考的是 2 的个数，但是如果题目换成 0门牌 的个数，那就不能简单地遍历了。因为像 1 号住户的门牌，实质上制作的时候，应该制作成 0001 ，有3个 0门牌。

所以这里隐藏了第二个考察点，就是字符串对齐操作和字符串补齐操作，具体来说，就是我们要把每一个字符串都用 0 填充到 4 位数全满，且原字符串需要右对齐。

对齐操作中，使用 > 表示右对齐，使用 < 表示左对齐，使用 ^ 表示居中对齐。

在对齐符号右边，可以写上对齐的范围（也可以不写），也就是目标字符串的长度，如 > 8 就是以8为范围向右对齐。

在对齐符号左边，可以写上填充字符串的内容（也可以不写），如 0 > 8 ，我们会用 0 去填充字符串中空余的部分。

利用上述两点，可以让 1， 11， 111 这样不足四位的数字也能以四位数的形式展现出来，方便统计 0 的个数。

res = 0
for num in range(1, 2021):
    res += format(num, '0>4').count('2')
print(res)
# 同样输出624

试题B：寻找2020

本题考察的点有两个，一个是如何按题目的意思去横向、纵向、斜向搜索2020，另一个是考察Python读取文件的操作。

由于是填空题，所以我也没有想什么优化的算法，就是简单的暴力搜索，写三个嵌套循环分别模拟三种搜索方式即可。

然后就是Python文件读取，我没什么比赛经验，但还是觉得涉及文件读取的题比较稀奇吧。

这部分知识也学过，大概注意几个点，打开文件后要记得关闭文件，如果不想这么麻烦的话就用with语句去控制文件的打开；然后就是读取文件数据的函数有好几个，我们应该根据题意去挑选合适的函数去读数据。

nums = []
res = 0
# 打开文件
with open('2020.txt') as f:
    for line in f.readlines():
        nums.append(line.split())
r, c = len(nums), len(nums[0])
# 搜横着的2020
for i in range(r):
    for j in range(c - 3):
        if nums[i][j] == '2' and nums[i][j+1] == '0' and nums[i][j+2] == '2' and nums[i][j+3] == '0':
            res += 1
# 搜竖着的2020
for i in range(r - 3):
    for j in range(c):
        if nums[i][j] == '2' and nums[i+1][j] == '0' and nums[i+2][j] == '2' and nums[i+3][j] == '0':
            res += 1
# 搜斜着的2020
for i in range(r-3):
    for j in range(c-3):
        if nums[i][j] == '2' and nums[i+1][j+1] == '0' and nums[i+2][j+2] == '2' and nums[i+3][j+3] == '0':
            res += 1
print(res)

这里因为没有2020.txt文件，所以我自己在本地随便写了一个规模小的同名文件测试，至少我那个小规模的用例是通过了的。

三次模拟时，要注意每一次的边界不同，切忌越界！仔细就行

试题C：跑步锻炼

本题的考察点是Python如何处理日期和遍历日期，这是两个问题，但可以用同一个模块来解决，那就是Python自带的datetime模块。

通过datetime模块可以快速定位起始日期和结束日期，求出两个日期之间的天数，然后利用timedelta去遍历起止日期之间的每一天，这一部分我看成是在遍历日期；然后在遍历每一天的过程中，需要判断这一天是否为周一或月初，这一部分我看成是在处理日期。

import datetime
res = 0
start = datetime.date(year=2000, month=1, day=1)
stop = datetime.date(year=2020, month=10, day=1)
for i in range((stop - start).days + 1):
    d = start + datetime.timedelta(days=i)
    res += 2 if d.day == 1 or d.isoweekday() == 1 else 1
print(res)

这里start和stop两个date类型的变量相减，结果是一个timedelta类型的值，这个timedelta的days属性表示起止日期间的天数，遍历天数再加到起始日期上即可达到遍历的效果。

另外还需要注意一个易混淆的点，就是判断date属于周几的函数有两个，一个isweekday()函数，另一个是此处用到的isoweekday()函数，两者的差别是，前者返回的结果用 0 ~ 6表示周一到周日，后者则是用 1 ~ 7来表示，个人觉得后者在使用上相对更人性化一点，所以选用了后者，其实没啥大的区别。

试题D：蛇形填数

博主对这种什么螺旋矩阵和蛇形填数的题非常不在行，基本算是不会解这类题。本题我是硬找规律解出来的。方法看看就好。

首先，题目的目标不难看出，是想求主对角线上的一个数，我们以要求的数为原点，向左下和右上延申，画一条斜线。假设要求的是第3行第3列的值，那我们就观察图中标出的这一部分（类似副对角线），画出来的这条线暂且称之为“目标线”吧。

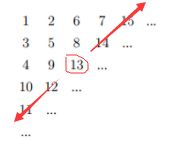
人坐着向左扭头45度，可以看到一个等腰三角形，从上到下每一层的元素个数分别是1，2，3，。。。

可以发现，我们要求第 i 行第 i 列的值，那么在“目标线”之上三角形的行数是 2 * i - 2，比如要求第3行第3列的值，那么在它之上的三角形有2 * 3 - 2 = 4行，共计 1+2+3+4=10个数.

知道上方三角形有10个数，那么“目标线”元素就是从11开始排序的。观察图片可以发现，确实“目标线”是从11开始排序的。且由于蛇形的特点，不管题目要求第几行第几列的值，“目标线”元素都是从左下开始向右上递增。

根据 第 i 行第 i 列可以得出，“目标线”的元素个数是 2 * i - 1，因此我们就知道了“目标线”上的元素从11开始遍历到 15 ，取11和15的中间数就是答案。

同样的套路应该到第20行第20列

up = 0
for i in range(1, 39):
    up += i
print(up)
# 输出741
print(up + 20)
# 输出761

这里输出741是“目标线”上方三角形中的元素总数， + 20是因为“目标线”的元素数为 2 * 20 -1 = 39，那么“目标线”元素就是 741 + 1 ~ 741 + 39，取中间数 741 + 20 = 761即是答案！

试题E：排序

本题考察的是冒泡排序的知识，需要对冒泡排序有一定程度的了解。

根据我自己的思路，首先要明确的一点是，冒泡排序中有两种动作或者说行为，一种是元素的“比较”，另一种是元素的“交换”；比较是不可避免一定会发生的，但是交换有可能发现也有可能不发生，本题需要聚焦的是“交换”。

第二点需要知道的是，对于长度为 n 的序列，第1轮遍历要进行 n-1 次比较，同时最多也会进行 n-1 次交换（因为交换是建立在比较的基础上嘛，先比较了才可能交换嘛），第2轮遍历要进行 n-2 次比较。。。第 n-1 轮要进行 1 次比较。

也就是说，长度为 n 的序列，冒泡排序需要进行 n-1 轮遍历，总共进行 n * (n - 1) // 2 次比较，最多也会发生这个多次交换。（顺带一提，取到最多交换次数的情况是序列全逆序，如 321、DCBA这样的序列）

明确了最大交换次数，那么就得到了最短可能进行100次交换的序列长度。

for l in range(1, 100):
    n += l
    if n >= 100:
        print(l, n)
        # 输出 14 和 105
        break
l += 1
# 此时 l 为 15

这段代码告诉我们什么呢？

那就是一个长度为15的序列，全逆序情况下进行冒泡排序会进行105次交换，就是这个样子：

['O', 'N', 'M', 'L', 'K', 'J', 'I', 'H', 'G', 'F', 'E', 'D', 'C', 'B', 'A']

那么现在多了5次，我们要对这个数组进行一些改动。
观察数组，我们想把 A 排到正确的位置需要14次交换，那是因为 A的前面有14个比A大的字母；我们想把 M 排到正确的位置需要进行2次交换，因为 M 前面有2个比 M 大的字母。

所以，改动的方法就呼之欲出了，我们只要让某个字母前面比它大的字母数比原来少 5 个，那把这个字母排到正确位置的交换数就会少 5 次，正好凑到100次。

以 A 为例，我们把 A 向前移动 5 位，移动到 G 和 F 之间：

['O', 'N', 'M', 'L', 'K', 'J', 'I', 'H', 'G', 'A', 'F', 'E', 'D', 'C', 'B']

此时会发现，A前面比A大的字母少了5个，只有9个了，而其他所有字母的交换数都不变，这样就实现了100次交换。

同理，B向前移动5位、C向前移动5位。。。都可以达到相同的交换数，也就是有很多相同长度的解。再看题目条件，长度相同的多个解输出字典序最小的那个。

这里也不难发现，如果采用移动 J 以后字母的方案，那么序列的首字母永远都是 O 。但是如果向前移动 J ，J的新位置则正好是序列首字母，此时字典序变小。因此，确定需要向前移动5位的字母是 J 。

答案就是：

['J', 'O', 'N', 'M', 'L', 'K', 'I', 'H', 'G', 'F', 'E', 'D', 'C', 'B', 'A']

顺便验算一下这个序列冒泡的交换次数是不是100，就当是复习冒泡排序了：

def bubblesort(s):
    b = len(s)-1
    res = 0
    while b >= 1:
        for i in range(b):
            if s[i] > s[i+1]:
                s[i], s[i+1] = s[i+1], s[i]
                res += 1
        b -= 1
    print(res)
bubblesort(['J', 'O', 'N', 'M', 'L', 'K', 'I', 'H', 'G', 'F', 'E', 'D', 'C', 'B', 'A'])
# 输出 100

试题F：成绩统计

本题考察的点有两个，一个是审题，或者说做题的经验吧，另一个就是Python小数点四舍五入的方法。

首先第一个审题问题，按照一般正常的逻辑，大于等于85的属于优秀，记到优秀数中；大于等于60的属于合格，记到合格数中去，你只能有一个成绩，要么就是优秀，要么就是合格，要么就是不合格。

由于有这三档成绩，而题目求的是优秀和合格两档的百分比，所以这两档的和应该小于等于100%。但是一看样例输出，71%和43%？？？这一求和都大于100%了，难道是题目出错了？

题目当然不会出错，之所以会出现这种“BUG”，是因为本题将大于等于85的人，既记到优秀数中，也同时记到合格数中，而大于等于60的人，只记到合格数中。这一点如果不仔细看样例输出，可能都察觉不到。

Python小数点四舍五入可以用round()函数，因为我们要输出整数百分比，所以四舍五入保留小数点后两位即可。

Python将小数按百分比格式输出可以用format进行格式化处理，只输出百分比的整数部分，所以{:.0%}即可

n = int(input())
scores = [int(input()) for _ in range(n)]
a, b = 0, 0
for i in range(n):
    if scores[i] >= 60:
        b += 1
        if scores[i] >= 85:
            a += 1
print('{:.0%}'.format(round(b / n, 2)))
print('{:.0%}'.format(round(a / n, 2)))

试题G：单词分析

本题考察的点有两个，一个是Python计数器类Counter的使用，另一个是Python排序和lambda表达式的使用。

由于题目求的是元素在序列中出现的次数，所以很自然地想到使用Python自带地itertools模块中的Counter类。

from collections import Counter
s = input()
c = Counter(s)
res = c.most_common()
print(res)
# 输出 [('o', 6), ('l', 4), ('n', 4), ('g', 4), ('i', 1), ('s', 1), ('t', 1)]

这段代码看似完美地解决了问题，我们只要取res的第一项就能得到答案，但是如果测试用例有两个以上的字母出现相同次数，且这个次数就是最大次数，那么就会出问题，比如下面这个用例，b 和 a都出现了2次。

'bbaac'
# 输出 [('b', 2), ('a', 2), ('c', 1)]

按照题目的要求，这种情况应该输出字典序较小的 a，但是却将 b 排在了第一个，所以我们还要对res进行排序。

排序的标准是，先对出现次数（元组的第二维）进行降序排序，再对元素的字典序（元组的第一维）进行升序排序。

能做到这一点的就是sort() 搭配 lambda表达式：

from collections import Counter
s = input() # 输入 bbaac
c = Counter(s)
res = c.most_common()
# 排序是这一步
res.sort(key=lambda x: (-x[1], x[0]))
print(res[0][0])
print(res[0][1])
# 输出 
# a 
# 2

至此才是本题较为健壮的解法。

试题H：数字三角形

本题考察的点有两个，一个是经典的动态规划，另一个是本题设置的额外条件。

我们暂且不看左右移动的次数限制。只关注DP的部分。

状态定义：dp[i][j] 定义为到达 nums[i][j] 时的最大总和

状态转移方程：dp[i][j] = max(dp[i-1][j-1], dp[i-1][i])

因为每一个位置的数字，只可能从上一层左侧的数字向右下移动得到，或者从上一层右侧的数字向左下移动得到。

另外，要注意，这个状态转移方程是一个通式，当 j = 0 时，上一层不存在左侧的数组，因此只能从上一层右侧的数字移动得来，同理，当 j = i 时，只能从上一层左侧数字移动得来

边界条件：dp[0][0] 位置的最大和即为nums[0][0]本身。

另外，由于dp[i][j]只和之前的dp和当前的nums有关，所以我们可以在原数组 nums 上进行DP，不需要使用额外空间。

n = int(input())
nums = [list(map(int, input().split())) for _ in range(n)]
for i in range(1, len(nums)):
    for j in range(len(nums[i])):
        if j == 0:
            nums[i][j] += nums[i-1][j]
        elif j == i:
            nums[i][j] += nums[i-1][j-1]
        else:
            nums[i][j] += max(nums[i-1][j-1], nums[i-1][j])

剩下的就是题目给出的左右移动次数限制，一开始会觉得可能需要维护一个二维DP，考虑左右次数差进行DP。但仔细一想其实没那么复杂。

当三角形的层数是奇数时，满足题目条件的目的地一定是最后一行的正中间。
当三角形的层数是偶数时，满足题目条件的目的地一定是最后一行中间两个数中较大的那个。
想要到达其他位置，都会不满足左右移动次数差不超过1的条件。

n = int(input())
nums = [list(map(int, input().split())) for _ in range(n)]
for i in range(1, len(nums)):
    for j in range(len(nums[i])):
        if j == 0:
            nums[i][j] += nums[i-1][j]
        elif j == i:
            nums[i][j] += nums[i-1][j-1]
        else:
            nums[i][j] += max(nums[i-1][j-1], nums[i-1][j])
print(max(nums[-1][n // 2 - 1], nums[-1][n // 2]) if n % 2 == 0 else nums[-1][n // 2])

试题I：平面切分

本题考察的是数学问题，包含一些动态规划的思想，还考验Python集合与元组的使用。

首先从规模最小的子问题开始观察，当 N == 1时，只有一条直线，那么dp[0] = 2 是固定的。

在观察 N == 2时，有两条直线，随者这两条直线之间关系的不同，dp值也会产生不同。

我们知道两条直线之间的位置关系有三种（我也不知道是不是就这三种，博主个人这类知识停留在初高中），分别是重合、平行和相交；而且，只要知道两条直线的斜率 a 和截距 b ，就可以明确他们之间的位置关系。

那么再回头看 dp[1]：
当两条直线重合时 dp[1] = dp[0]
当两条直线平行时 dp[1] = dp[0] + 1， 此时直线的交点数为 0
当两条直线相交时 dp[1] = dp[0] + 2， 此时直线的交点数为 1

从直观的角度看，感觉切片的空间数是不是和直线交点数有关系呢？？？暂且先这样猜测。

那么，现在以 dp[i]为例，当我们的空间中已经有 i -1条直线，现在准备往空间中加入第 i 条直线。

可以发现：
1）重合，当新加入的直线 i 与原本空间中存在的 i-1 条直线中的某一条重合时，相当于没有加入新的直线，所以dp[i] = dp[i-1]

2）平行，当新加入的直线 i 与原本空间中存在的 i-1 直线中的一些直线平行时，直线 i 和 这些平行的直线没有产生新的交点，交点数不变。

3）相交，当新加入的直线 i 与原本空间中存在的 i-1 直线中的一些直线相交时，每和一条直线相交，则会使交点数 +1。

至此，我们可以得出大致的状态转移方程：

当直线 i 与 直线 1~i-1 中的任意一条重合时：
dp[i] = dp[i-1]

当直线 i 与 直线 1~i-1 中的任意一条都不重合时：
dp[i] = dp[i-1] + 直线 i 与 直线1~i-1之间产生的交点数 + 1

同时，解题过程中，需要维护一个存放交点的集合！
就拿样例输入来说，（1，1）（2，2）（3，3）这三条直线两两相交，但是最终只会有 1 个交点，因为三条直线相交在同一点上，所以我们需要对每两条直线可能产生的交点进行去重。

n = int(input())
lines = []
for _ in range(n):
    a, b = list(map(int, input().split()))
    lines.append((a, b))
dp = [2 for _ in range(n)]
for i in range(1, n):
    pot = 0
    pots = set()
    for j in range(i):
        # 重合
        if lines[i][0] == lines[j][0] and lines[i][1] == lines[j][1]:
            pot = -1
            break
        # 平行不重合
        elif lines[i][0] == lines[j][0] and lines[i][1] != lines[j][1]:
            continue
        # 相交
        elif lines[i][0] != lines[j][0]:
            # 交点的横坐标
            x = (lines[i][1] - lines[j][1]) / (lines[j][0] - lines[i][0])
            # 交点的纵坐标
            y = x * lines[j][0] + lines[j][1]
            # 交点存到集合中
            pots.add((x, y))
            pot = len(pots)
    dp[i] = dp[i-1] + (pot + 1)
print(dp[-1])
# 样例输出 6

如果不进行交点去重，而直接通过斜率和截距去判断交点数，本题的样例是通过不能的！！！下面是博主最早写的版本，很好的说明了这个问题：

n = int(input())
lines = []
for _ in range(n):
    a, b = list(map(int, input().split()))
    lines.append((a, b))
dp = [2 for _ in range(n)]
for i in range(1, n):
    pot = 0
    for j in range(i):
        # 重合
        if lines[i][0] == lines[j][0] and lines[i][1] == lines[j][1]:
            pot = -1
            break
        # 平行不重合
        elif lines[i][0] == lines[j][0] and lines[i][1] != lines[j][1]:
            continue
        # 相交
        elif lines[i][0] != lines[j][0]:
            pot += 1
    dp[i] = dp[i-1] + (pot + 1)
print(dp[-1])
# 样例输出 7，同一个交点判定了两次，所以答案也多了1

这里还需要点出一点：就是博主本题写的代码，应该是有缺陷的。为什么呢？因为我先后将代码放在三个平台上提交过：
1）蓝桥杯练习系统，10个用例只通过7个
2）AcWing，10个用例只通过7个
3）蓝桥云课，10个用例全部通过

遇到这种情况，我就去看了CSDN上其他人的优秀代码，发现逻辑上其实都差不多，但是他们的代码就是能全部提交通过，而我的就不行。关于这一点博主我现在也还没有找到原因。

试题J：装饰珠

这个压轴题考察的是动态规划，当然暴搜应该也可以的一些分数。博主这边自己想是想不出来的，所以查阅了非常多站内的题解，发现至少一般以上的题解这一题都是空着的，说明难度确实有，而且是那种给你答案都不一定看得懂的难度。所以，这更激发了博主至少要看题解看懂本题的决心。

我看的题解中，对我启发最大的是一篇Java写的题解，他除了代码以外，还较为详细地描述了DP的状态定义和状态转移方程，代码中用到的一些变量也做了说明：

然后，我个人觉得，这篇解析中最关键的就是 s 的意义，但不知道什么原因，这篇博客关键的一行显示不出来。

原帖地址在这里

难点分析：
1）题目非常长，好像ACM那种题都是这种风格吧？我不是很清楚，做过几次ACM的练习赛和模拟赛，感觉这种把题目本题隐藏在一个所谓的实际场景的题，最难读懂。

2）输入非常多，且输入的顺序不是解题最佳的顺序，我们不仅要小心地编写输入代码，还要在输入后处理成方便解题的格式或者说结构。

3）动态规划状态转移方程。转移方程本身不难，但对于一些“特殊”情况的考虑如果不周到，很容易求出错的解。

A = [list(map(int, input().split())) for _ in range(6)]
m = int(input())
B = [list(map(int, input().split())) for _ in range(m)]
# 处理孔的信息
holes = [A[i][j] for i in range(6) for j in range(1, len(A[i]))]
holes.sort()
# 处理珠的信息
# 各个珠的等级
ball_grades = [B[i][0] for i in range(m)]
# 各个珠子的价值
ball_values = [B[i][2:] for i in range(m)]
# 各个珠子的数量
ball_nums = [0 for _ in range(m)]
# 开辟DP数组
dp = [[0 for _ in range(len(holes))] for _ in range(m)]
# 边界条件
# dp[0][0]的情况
if holes[0] >= ball_grades[0]:
    dp[0][0] = ball_values[0][0]
    ball_nums[0] += 1
# dp[0][j]的情况
for j in range(1, len(holes)):
    if holes[j] >= ball_grades[0]:
        if ball_nums[0] >= len(ball_values[0]):
            dp[0][j] = dp[0][j-1]
        else:
            if dp[0][j-1] > ball_values[0][ball_nums[0]]:
                dp[0][j] = dp[0][j-1]
            else:
                dp[0][j] = ball_values[0][ball_nums[0]]
                ball_nums[0] += 1
# dp[i][0]的情况
for i in range(1, m):
    if holes[0] >= ball_grades[i]:
        if ball_nums[i] >= len(ball_values[i]):
            dp[i][0] = dp[i - 1][0]
        else:
            # 放与不放
            dp[i][0] = dp[i-1][0] + ball_values[i][ball_nums[i]]
            ball_nums[i] += 1
    else:
        dp[i][0] = dp[i-1][0]
# 常规DP
for i in range(1, m):
    t2 = 0
    s = 0
    for j in range(1, len(holes)):
        if holes[j] >= ball_grades[i]:
            t2 += 1
            if t2 == 1:
                s = j - 1
            maxlim = ball_values[i][-1] if t2 > len(ball_values[i]) else ball_values[i][t2-1]
            dp[i][j] = max(dp[i-1][j], dp[i][s]+maxlim)
        else:
            dp[i][j]=dp[i-1][j]
print(dp[-1][-1])

用Python处理输入信息非常简便，常规DP部分也很简单，复杂的是边界条件的书写。奇怪的是，我的代码在蓝桥杯练习系统中一个都过不了，但是蓝桥云课上却能全通过。所以我的代码应该还有问题，之后会改！