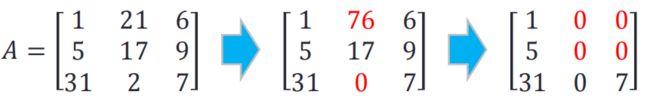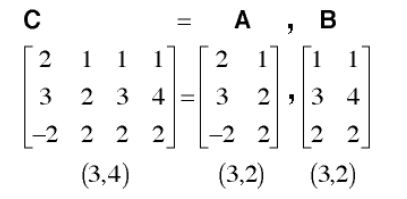【MATLAB 入门指南 一】基本操作与矩阵输入

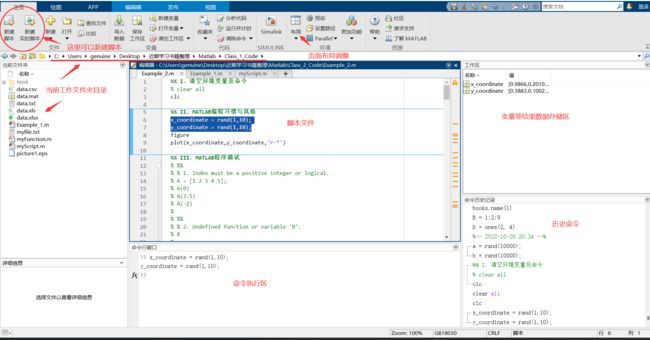
1.MATLAB 主界面

• 如果语句以分号结束，MATLAB 会执行计算，但不在命令行窗口中显示输出。
• 在空白命令行中按向上 (↑) 和向下箭头键 (↓) 可以重新调用以前的命令。
• 在键入命令的前几个字符之后按箭头键。例如，要重新调用命令 b = 2，请键入 b，然后按向上箭头键，会调出以 b 开头的所有历史命令

2. MATLAB 基本语法

2.1 变量

• MATLAB 中的变量不需要声明.
• 使用 = 为变量赋值
• 如果未指定输出变量，MATLAB 将使用变量 ans（answer 的缩略形式）来存储计算结果。

2.2 变量名

• 变量名对大小写敏感；
• 变量名的第一个字符必须为英文字母，其长度不能超过 31 个字符；
• 变量名可以包含_、数字，但不能包含空格符、标点；

MATLAB 中有一些变量有其具体意义,不适合用作变量名.

变量	意义
ans	上一句的运算的结果
i 和 j	复数算子
inf	无穷 ∞
eps	浮点相对精度,即 1.0 到下一个浮点数之间的距离(值为2.2204e-16)
NaN	非数字
pi	圆周率 π
realmin	最小浮点数 2−1022
realmax	最大浮点数 (2−ε)21023

• 通过将非零值除以零或计算明确定义的溢出（即超过 realmax）的数学表达式，会生成无穷值。通过尝试计算 0/0 或 Inf-Inf 等没有明确定义的数值的表达式，会生成非数字

>> 0/0

ans =

   NaN

>> 5/0

ans =

   Inf

复数

复数包含实部和虚部，虚数单位是 -1 的平方根

>> sqrt(-1)

ans =

   0.0000 + 1.0000i

用 i 或者 j 表达虚部，用 j 最终的结果均为 i 来表达

>> c = [3+4i, 4+3j; -i, 10j]

c =

   3.0000 + 4.0000i   4.0000 + 3.0000i
   0.0000 - 1.0000i   0.0000 +10.0000i

除此以外,使用 iskeyword 命令可以查看 MATLAB 语言所有的关键字,这些关键字也不允许被用作变量名：

break、case、catch、classdef、continue、else、elseif、end、for、function、global、if、otherwise、parfor、persistent、return、spmd、switch、try、while

2.3 MATLAB 调用优先级

>> cos='This string'; % 注意这里是单引号，双引号表示字符串
cos(8)

ans =

    'r'

这里并没有触发内置函数 cos 的执行，而是当作了一个字符串变量

此时，若某函数被变量名所覆盖,则调用 clear <变量名> 可以取消绑定在该函数名上的变量名，并将此变量从工作区中清除

>> clear cos	% 清除绑定在 cos 上的变量
>> cos(8)		% 调用内置余弦函数运算得到-0.1455

ans =

   -0.1455

注：clear 是一个比较危险的命令,因为该命令后若不加参数,则表示清除当前工作区内的所有变量.

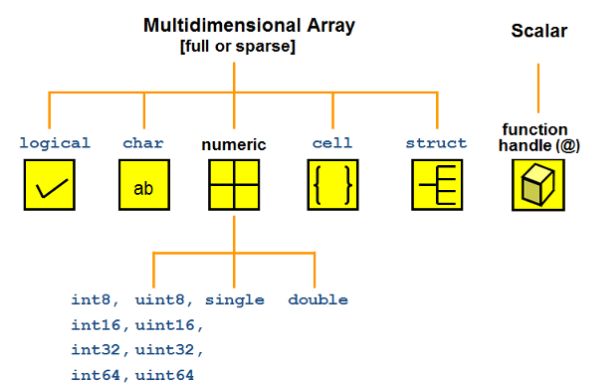
2.4 变量的类型

MATLAB 中的变量类型有： logical，char，numeric，cell、struct 以及由他们组成的数组或矩阵

2.5 numeric 型变量的显示格式

我们直接定义的数字型变量,默认是以 double 形式存储的.

我们可以通过 format <显示格式> 改变数字型变量的显示格式.

显示格式	说明	例子
short	短定点格式.显示小数点后 4 位	3.1416
long	固定的十进制格式,double类型变量显示小数点后15位,对float类型变量显示小数点后7位.	3.141592653589793
shortE	小数点后有4位数的短科学记数法	3.1416e+00
longE	长科学计数法.对double类型变量显示小数点后15位,对float类型变量显示小数点后7位.	3.141592653589793e+00
bank	小数点后有两位的货币格式	3.14
hex	十六进制格式	400921fb54442d18
rat	比例格式	355/113

>> format long
>> pi

ans =

   3.141592653589793

>> format bank
>> pi

ans =

          3.14

>> format rat
>> pi

ans =

     355/113   

运算实例：$\frac{1}{2}$ + $\frac{1}{3}$ + $\frac{1}{4}$

>> 1/2 + 1/3 + 1/4

ans =

    1.0833

>> format longE
>> ans

ans =

     1.083333333333333e+00

>> format rat
>> ans

ans =

      13/12   

2.6 MATLAB命令行

• 行尾;在一行命令后使用可以使得此句不输出结果，仅保存在工作区
• 其他命令：

命令	作用
clc	清除命令行窗口的所有命令
clear	清除当前工作区内所有变量
clear <变量名>	清除工作区指定变量
who	列出工作区中的变量
whos	列出工作区中的变量及大小和类型

3. MATLAB 数字运算

3.1 使用 MATLAB 计算数学表达式

• 运算的优先级规则：同等优先级下从左向右运算，优先级顺序从高到低：
  • 括号()
  • 乘方^
  • 乘除法*，/
  • 加减法+，-

数学表达式求值实例：

数学表达式	MATLAB命令
cos($\frac{\sqrt{(1+2+3+4{)}^3}}{5}$)	cos(sqrt((1+2+3+4)^3/5))
sin($\sqrt{\pi }$) + ln(tan(1))	sin(sqrt(pi))+log(tan(1))
$2^{3.5\times 1.7}$	2^(3.5*1.7)
$e^{sin(10)}$	exp(sin(10))

3.2 MATLAB 内置的数学函数

• 运算符与基本运算

• 初等数学

4. MATLAB 矩阵运算

4.1 矩阵定义与向量运用

4.1.2 矩阵定义

• 在 MATLAB 中，使用 [] 将待输入的矩阵内容括起来，使用空格 或逗号,分隔行内变量,使用;分隔每一行.

矩阵的定义：

MATLAB 命令	结果
标量： 3	3
行向量： [1 2 3 4]	$\left[\begin{array}{ccc}1& 2& 3\end{array}\right]$
列向量： [1; 2; 3; 4]	$\left[\begin{array}{c}1\\ 2\\ 3\\ 4\end{array}\right]$
矩阵： [1 21 6; 5 17 9; 31 2 7]	$\left[\begin{array}{ccc}1& 21& 6\\ 5& 17& 9\\ 31& 2& 7\end{array}\right]$

4.1.2 使用:运算符创建向量

使用冒号运算符:可以创建一个长向量,其语法如下:

冒号表达式	结果
i:j	$\left[\begin{array}{ccccc}i,& i+1,& i+2,& ...,& j\end{array}\right]$
i:k:j	$\left[\begin{array}{cccccc}i,& i+k,& i+2k,& i+3k,& ...,& j\end{array}\right]$

冒号运算符使用：

MATLAB命令	结果
2:5	$\left[\begin{array}{cccc}2& 3& 4& 5\end{array}\right]$
2:2:5	$\left[\begin{array}{cc}2& 4\end{array}\right]$
[1:5; 2:3:15; -2:0.5:0]	$\left[\begin{array}{ccccc}1& 2& 3& 4& 5\\ 2& 5& 8& 11& 14\\ -2& -1.5& -1& -0.5& 0\end{array}\right]$
'a':2:'z'	‘acegikmoqsuwy’

4.1.3 函数生成矩阵

MATLAB命令	结果
eye(n)	n × n 的单位矩阵
zeros(n1, n2)	n1 × n2 的零矩阵
ones(n1, n2)	n1 × n2 的全 1 矩阵
diag(vector)	得到一个以向量vector中内容为对角线的对角矩阵
linspace(x1,x2,n)	生成区间为[x1, x2]，有 n 个点的等差数列
magic(n)	生成 n × n 的幻方矩阵
rand	均匀分布的随机数
randn	正态分布的随机数

• 矩阵和数组

4.2 矩阵的索引

• MATLAB 中的矩阵是以列先序存储的.且索引下标从1开始.
• 矩阵有两种索引方式: 按一维索引和按二维索引.对于一个一般的矩阵,其索引顺序如下:
  $$\left[\begin{array}{ccc}1或(1,1)& 4或(1,2)& 7或(1,3)\\ 2或(2,1)& 5或(2,2)& 8或(2,3)\\ 2或(3,1)& 6或(3,2)& 9或(3,3)\end{array}\right]$$
• 矩阵的索引可以使用冒号:,选取向量范围内的值
• 矩阵的索引可以是一个或两个向量,表示选中向量内的所有行或所有列.

矩阵索引的规则:

原矩阵	索引	结果	说明
A = $\left[\begin{array}{ccc}1& 2& 3\\ 4& 5& 6\\ 7& 8& 9\end{array}\right]$	A(8)	6	以列开始，取第 8 个元素 (线性索引)
A = $\left[\begin{array}{ccc}1& 2& 3\\ 4& 5& 6\\ 7& 8& 9\end{array}\right]$	A([1 3 5])	$\left[\begin{array}{ccc}1& 7& 5\end{array}\right]$	取矩阵第 [1 3 5] 位置元素放入新矩阵的对应位置
A = $\left[\begin{array}{ccc}1& 2& 3\\ 4& 5& 6\\ 7& 8& 9\end{array}\right]$	A([1 2; 3 4])	$\left[\begin{array}{cc}1& 4\\ 7& 2\end{array}\right]$	取矩阵第 [1 2; 3 4] 位置元素放入新矩阵的对应位置
A = $\left[\begin{array}{ccc}1& 2& 3\\ 4& 5& 6\\ 7& 8& 9\end{array}\right]$	A(3,2)	8	取矩阵第 3 行，第 2 列
A = $\left[\begin{array}{ccc}1& 2& 3\\ 4& 5& 6\\ 7& 8& 9\end{array}\right]$	A([1,2], :)	$\left[\begin{array}{ccc}1& 2& 3\\ 4& 5& 6\end{array}\right]$	取矩阵第[1,2]行的所有元素
A = $\left[\begin{array}{ccc}1& 2& 3\\ 4& 5& 6\\ 7& 8& 9\end{array}\right]$	A([1 3], [1 2])	$\left[\begin{array}{cc}1& 2\\ 7& 8\end{array}\right]$	取矩阵第[1 3]行，第[1 2]列的交叉项

注意：

1. 引用数组外部元素，MATLAB 会引发错误

>> A = [1 2 3 4; 5 6 7 8; 9 10 11 12; 13 14 15 16]

A =

     1     2     3     4
     5     6     7     8
     9    10    11    12
    13    14    15    16

>> A(4,5)
Index in position 2 exceeds array bounds. Index must not exceed 4.

• 不过，可以在赋值语句左侧指定当前维外部的元素。数组大小会增大以便容纳新元素

>> A = [1 2 3 4; 5 6 7 8; 9 10 11 12; 13 14 15 16]

A =

     1     2     3     4
     5     6     7     8
     9    10    11    12
    13    14    15    16

>> A(4,5) = 17

A =

     1     2     3     4     0
     5     6     7     8     0
     9    10    11    12     0
    13    14    15    16    17

4.3 矩阵的操作

4.3.1 值的改变

实例分析:

>> A = [1 21 6; 5 17 9; 31 2 7]

A =

       1             21              6       
       5             17              9       
      31              2              7       

>> A(1,2)=76

A =

       1             76              6       
       5             17              9       
      31              2              7       

>> A(3,2)=0

A =

       1             76              6       
       5             17              9       
      31              0              7       

>> A([1 2], [2 3]) = 0

A =

       1              0              0       
       5              0              0       
      31              0              7    

4.3.2 删除操作

删除某行或某列实例:

A =

       1              0              0       
       5              0              0       
      31              0              7   

>> A(3,:)

ans =

      31              0              7       

>> A(3,:) = []

A =

       1              0              0       
       5              0              0    

• 如果删除矩阵中的单个元素，结果将不再是矩阵，将会导致错误

>> x = [1 2 3; 4 5 6; 7 8 9]

x =

     1     2     3
     4     5     6
     7     8     9

>> x(1, 2) = []
空赋值只能具有一个非冒号索引。

• 使用单一下标可以删除一个元素或元素序列，并将其余元素重构为一个行向量

>> x(1:2:9) = []

x =

     4     2     8     6

4.3.3 矩阵拼接

• 使用 , 将彼此相邻的数组串联起来称为水平串联，每个数组必须具有相同的行数
• 如果各数组具有相同的列数，则可以使用; 垂直串联

拼接实例:

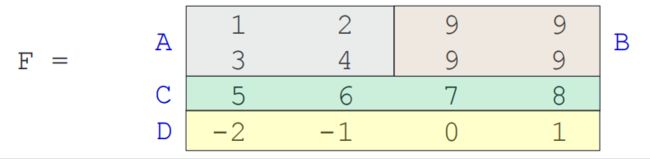
• F = [A B; C; D] 表示把 A、B、C、D 放在一起形成一个新的增广矩阵

>>  A=[1 2;3 4]

A =

       1              2       
       3              4       

>> B=[9 9;9 9]

B =

       9              9       
       9              9       

>> C = [5 6 7 8]

C =

       5              6              7              8       

>> D = [-2 -1 0 1]

D =

      -2             -1              0              1       

>> F = [A B; C; D]

F =

       1              2              9              9       
       3              4              9              9       
       5              6              7              8       
      -2             -1              0              1  

4.3.5 矩阵运算符操作

运算符	操作	形式	例子
+	矩阵与向量相加	A+B	[6 3] + 2 = [8 5]
+	矩阵与矩阵对应位置相加	A+B	[6 3] + [4 8] = [10 11]
-	矩阵与向量相减	A-B	[6 3] - 2 = [4 1]
-	矩阵与矩阵对应位置相减	A-B	[6 3] - [4 8] = [2 -5]
*	矩阵乘法	A*B	[6 3] * [4 8]' = 48
.*	矩阵与矩阵对应位置相乘	A.*B	[6 3] * [4 8] = [24 24]
/	矩阵与矩阵右除(等价于A*inv(B))	A/B	[6 3] / [4 8] = 0.6
\	矩阵与矩阵左除(等价于inv(A)*B)	A\B	[6 3] / [4 8] = [0.06667 1.3333; 0 0]
./	矩阵与矩阵对应位置右除	A./B	[6 3] ./ [4 8] = [1.5 0.375]
.\	矩阵与矩阵对应位置左除	A.\B	[6 3] .\ [4 8] = [0.6667 2.6667]
'	矩阵的转置	A'	[6 3]' = [6; 3]
^	矩阵与向量乘方	A^B	[1 2; 3 4]^3 = [37 54; 81 118]
.^	矩阵与矩阵对应位置乘方	A.^B	[1 2; 3 4].^[1 2; 3 4] = [1 4; 27 256]

4.3.6 逻辑下标

• 仅提取 x 中正常的数值

>> x = [2.1 1.7 1.6 1.5 NaN 1.9 1.8 1.5 5.1 1.8 1.4 2.2 1.6 1.8];
>> L = isfinite(x)

L =

  1×14 logical 数组

   1   1   1   1   0   1   1   1   1   1   1   1   1   1

>> x(L)

ans =

  列 1 至 10

    2.1000    1.7000    1.6000    1.5000    1.9000    1.8000    1.5000    5.1000    1.8000    1.4000

  列 11 至 13

    2.2000    1.6000    1.8000

• 提取比均值大三倍标准差的元素

>> x = [2.1 1.7 1.6 1.5 NaN 1.9 1.8 1.5 5.1 1.8 1.4 2.2 1.6 1.8];
>> x = x(isfinite(x));
>> x = x(abs(x-mean(x)) <= 3*std(x))

x =

  列 1 至 10

    2.1000    1.7000    1.6000    1.5000    1.9000    1.8000    1.5000    1.8000    1.4000    2.2000

  列 11 至 12

    1.6000    1.8000

• 将非质数设置为 0

>> x = [1 2 3; 4 5 6; 7 8 9]

x =

     1     2     3
     4     5     6
     7     8     9

>> x(~isprime(x)) = 0

x =

     0     2     3
     0     5     0
     7     0     0

4.3.7 矩阵操作的相关函数

• 描述性统计量

• 线性代数

常用函数:

函数	作用	说明文档
max	数组的最大元素	点击跳转
sum	数组元素总和	点击跳转
sort	对数组元素排序	点击跳转
sortrows	对矩阵行或表行进行排序	点击跳转
size	数组大小	点击跳转
find	查找非零元素的索引和值	点击跳转
perms	产生所有可能的排列

• find 函数：选取 x 矩阵中质数的位置

>> x = [1 2 3; 4 5 6; 7 8 9]

x =

     1     2     3
     4     5     6
     7     8     9

>> k = find(isprime(x))'

k =

     3     4     5     7

• 使用以下命令按 k 确定的顺序将这些质数显示为行向量

>> x(k)

ans =

     7     2     5     3

• 将 k 用作赋值语句的左侧索引时，会保留矩阵结构：

>> x(k) = NaN

x =

     1   NaN   NaN
     4   NaN     6
   NaN     8     9

4.4 高维矩阵

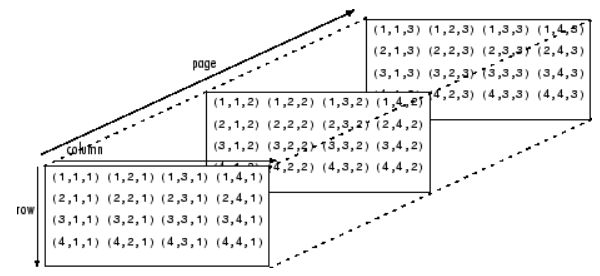
• 先创建二维矩阵

>> A = [1 2 3; 4 5 6; 7 8 9]

A =

     1     2     3
     4     5     6
     7     8     9

• 添加第二页

>> A(:,:,2) = [10 11 12; 13 14 15; 16 17 18]

A(:,:,1) =

     1     2     3
     4     5     6
     7     8     9


A(:,:,2) =

    10    11    12
    13    14    15
    16    17    18

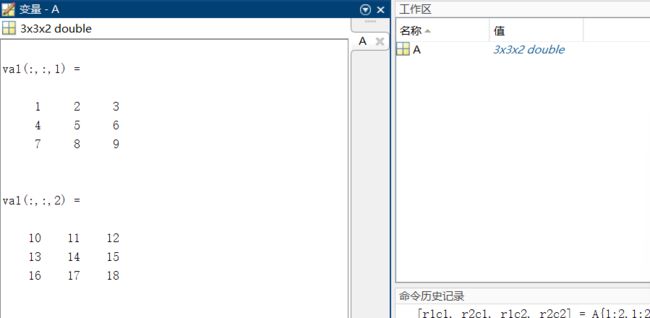
• cat(dim, A, B) 函数可用于构造多维数组

>> B = cat(3,A,[3 2 1; 0 9 8; 5 3 7])

B(:,:,1) =

     1     2     3
     4     5     6
     7     8     9


B(:,:,2) =

    10    11    12
    13    14    15
    16    17    18


B(:,:,3) =

     3     2     1
     0     9     8
     5     3     7

• 快速扩展多维数组的另一种方法是将一个元素赋给一整页

>> B(:,:,4) = 0

B(:,:,1) =

     1     2     3
     4     5     6
     7     8     9


B(:,:,2) =

    10    11    12
    13    14    15
    16    17    18


B(:,:,3) =

     3     2     1
     0     9     8
     5     3     7


B(:,:,4) =

     0     0     0
     0     0     0
     0     0     0

高维数组中元素的访问

>> A

A(:,:,1) =

     1     2     3
     4     5     6
     7     8     9


A(:,:,2) =

    10    11    12
    13    14    15
    16    17    18

• 只访问 A 的每一页上的第一列和第三列

>> C = A(:,[1 3],:)

C(:,:,1) =

     1     3
     4     6
     7     9


C(:,:,2) =

    10    12
    13    15
    16    18

操作高维数组

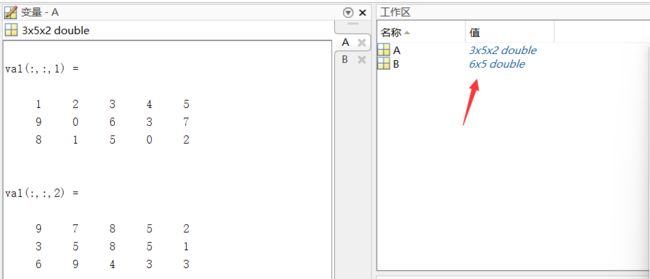
• reshape：reshape 逐列操作，沿 A 中各列连续逐一提取元素来创建新矩阵，从第一页开始，之后是第二页

>> A = [1 2 3 4 5; 9 0 6 3 7; 8 1 5 0 2];
A(:,:,2) = [9 7 8 5 2; 3 5 8 5 1; 6 9 4 3 3];
>> B = reshape(A,[6 5])

B =

     1     3     5     7     5
     9     6     7     5     5
     8     5     2     9     3
     2     4     9     8     2
     0     3     3     8     1
     1     0     6     4     3

• permute

>> M(:,:,1) = [1 2 3; 4 5 6; 7 8 9];
M(:,:,2) = [0 5 4; 2 7 6; 9 3 1]

M(:,:,1) =

     1     2     3
     4     5     6
     7     8     9


M(:,:,2) =

     0     5     4
     2     7     6
     9     3     1

• 使用 permute 函数，通过在第二个参数中指定维度顺序，将每一页上的行下标和列下标交换。M 的原始行现在是列，原始列现在是行。

>> P1 = permute(M,[2 1 3])

P1(:,:,1) =

     1     4     7
     2     5     8
     3     6     9


P1(:,:,2) =

     0     2     9
     5     7     3
     4     6     1

• 将 M 的行下标和页下标交换

>> P2 = permute(M,[3 2 1])

P2(:,:,1) =

     1     2     3
     0     5     4


P2(:,:,2) =

     4     5     6
     2     7     6


P2(:,:,3) =

     7     8     9
     9     3     1

• repmat 函数：创建一个 2×3×1×4 数组

>> A = repmat(5,[2 3 1 4])

A(:,:,1,1) =

     5     5     5
     5     5     5


A(:,:,1,2) =

     5     5     5
     5     5     5


A(:,:,1,3) =

     5     5     5
     5     5     5


A(:,:,1,4) =

     5     5     5
     5     5     5

>> size(A)

ans =

     2     3     1     4

• squeeze 函数：消除长度为 1 的维度

>> B = squeeze(A)

B(:,:,1) =

     5     5     5
     5     5     5


B(:,:,2) =

     5     5     5
     5     5     5


B(:,:,3) =

     5     5     5
     5     5     5


B(:,:,4) =

     5     5     5
     5     5     5

>> size(B)

ans =

     2     3     4

4.5 构建表

>> n = (0:9)';
>> pows = [n  n.^2  2.^n]

pows =

     0     0     1
     1     1     2
     2     4     4
     3     9     8
     4    16    16
     5    25    32
     6    36    64
     7    49   128
     8    64   256
     9    81   512

注意事项

MATLAB 命令	说明
diary	将命令行窗口文本记录到日志文件中
home	发送光标复位
commandwindow	选择命令行窗口
commandhistory	打开命令历史记录窗口

• 新手容易犯错，打开 MATLAB 之后，请按 CTRL+Q 这个组合键，是不是发现MATLAB关闭了？

Reference

[1] MATLAB 官方文档

[2] MATLAB01:基本的数学运算与矩阵运算

[3] MATLAB（一）基本操作与矩阵输入

[4] MATLAB使用教程（一）——从零开始，基础，数据类型——新手来看

[5]【经验分享】CSDN如何修改文字的字体、大小以及颜色

[6] CSDN如何编辑数学公式