机器学习笔记之正则化(一)拉格朗日乘数法角度

引言

从本节开始，将介绍正则化，并从拉格朗日乘数法角度进行观察。

回顾：基于正则化的最小二乘法

在处理线性回归任务过程中，我们以$L_2$正则化($\text{Regularization}$)为例介绍了正则化在最小二乘法损失函数的作用。

关于最小二乘估计关于权重$\mathcal{W}$的矩阵形式表达公式表示如下：
$$\{\begin{array}{l}\mathcal{L}(\mathcal{W})={\mathcal{W}}^T{\mathcal{X}}^T\mathcal{X}\mathcal{W}-2{\mathcal{W}}^T{\mathcal{X}}^T\mathcal{Y}+{\mathcal{Y}}^T\mathcal{Y}\\ \hat{\mathcal{W}}=\underset{\mathcal{W}}{\mathrm{argmin}}\mathcal{L}(\mathcal{W})\end{array}$$
对$\mathcal{L}(\mathcal{W})$关于$\mathcal{W}$求解偏导，求解最优值$\hat{\mathcal{W}}$：
$$\{\begin{array}{l}\begin{array}{r}\frac{\partial \mathcal{L}(\mathcal{W})}{\partial \mathcal{W}}=2{\mathcal{X}}^T\mathcal{X}\mathcal{W}-2{\mathcal{X}}^T\mathcal{Y}\triangleq 0\end{array}\\ \hat{\mathcal{W}}=({\mathcal{X}}^T\mathcal{X}{)}^{-1}{\mathcal{X}}^T\mathcal{Y}\end{array}$$
关于$L_2$正则化的最小二乘估计$\mathcal{L}(\mathcal{W},\lambda )$表示为：
$$\mathcal{L}(\mathcal{W},\lambda )={\mathcal{W}}^T{\mathcal{X}}^T\mathcal{X}\mathcal{W}-2{\mathcal{W}}^T{\mathcal{X}}^T\mathcal{Y}+{\mathcal{Y}}^T\mathcal{Y}+\lambda {\mathcal{W}}^T\mathcal{W}$$
对应最优解表示为：
$$\hat{\mathcal{W}}=({\mathcal{X}}^T\mathcal{X}+\lambda \mathcal{I}{)}^{-1}{\mathcal{X}}^T\mathcal{Y}$$
关于前后加正则化的权重最优解对比发现，在$N$阶方阵${\mathcal{X}}^T\mathcal{X}$每个主对角线元素中添加了一个$\lambda$。这样能够保证${\mathcal{X}}^T\mathcal{X}$必然是正定矩阵，而不单是实对称矩阵。如果 ${\mathcal{X}}^T\mathcal{X}$不是满秩矩阵，从而无法求解矩阵的逆${\Lambda }^{-1}$：
其中$\mathcal{Q}$表示正交矩阵。
$${\mathcal{X}}^T\mathcal{X}=\mathcal{Q}\Lambda {\mathcal{Q}}^T$$

正则化描述

正则化的优化对象

正则化，本质上是一种减少过拟合的方法。在神经网络中，关于正则化的描述是指关于权重$\mathcal{W}$的正则化。在神经网络中，参数分为两类：权重$(\text{Weight})$、偏置$(\text{Bias})$。

• 权重影响的是神经网络所逼近函数的形状；而偏置影响的是函数的位置信息。在神经网络学习过程中，一旦对权重进行约束，偏置也会随之进行调整。因此对偏置进行约束意义不大。

• 从$\text{M-P}$神经元的角度观察，偏置本身就是激活神经元的阈值。而阈值可看作是某权重与对应哑结点($\text{Dummy Node}$)的线性结果，因而可以在学习过程中将阈值的学习包含在权重中(${\mathcal{W}}_{\text{Dum}}\in \mathcal{W}$)：
  $$\theta ={\mathcal{W}}_{\text{Dum}}\cdot \underset{\text{fixed}=-1}{x_{\text{Dum}}}$$

因此，正则化的优化对象是权重参数$\mathcal{W}$。

常见的正则化方法

常见的正则化方法是$L_1,L_2$正则化。这里的$L_1,L_2$是指对应范数的类型。以$L_2$范数为例。假设某权重$\mathcal{W}$是一个$p$维向量：
$$\mathcal{W}=(w_1,w_2,\cdots ,w_p{)}^T$$
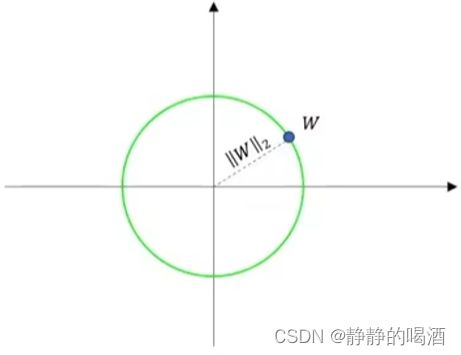
而$\mathcal{W}$可看作是$p$维特征空间中的一个具体的点。而$L_2$范数表示该点$\mathcal{W}$到$p$维特征空间原点之间的距离：
$$\begin{array}{rl}||\mathcal{W}|{|}_2& =\sqrt{(w_1-0{)}^2+(w_2-0{)}^2+\cdots +(w_p-0{)}^2}\\ & =\sqrt{|w_1{|}^2+|w_2{|}^2+\cdots +|w_p{|}^2}\end{array}$$

以二维特征为例。此时的${\mathcal{W}}^{(2)}$表示为：$\begin{array}{r}{\mathcal{W}}^{(2)}=(w_1,w_2{)}^T\end{array}$。关于${\mathcal{W}}^{(2)}$的$L_2$范数$||{\mathcal{W}}^{(2)}|{|}_2$可表示为：
$$||{\mathcal{W}}^{(2)}|{|}_2=\sqrt{|w_1{|}^2+|w_2{|}^2}$$
满足到$p$维特征空间原点之间距离为$||{\mathcal{W}}^{(2)}|{|}_2$的$\mathcal{W}$的集合在图像中表示的形状是一个圆，这意味着在圆上的每一个点都表示其特征满足$L_2$范数结果相同的权重：

• 圆形状仅仅是二维特征的一个描述。随着维度增加，其形状是球、以及超球体。
• 该图像视频链接见末尾，侵删，下同。
  

同理，$L_1$正则化对应的$L_1$范数表示如下：
$$||\mathcal{W}|{|}_1=|w_1|+|w_2|+\cdots +|w_p|$$
依然以二维权重特征$||{\mathcal{W}}^{(2)}|{|}_1=|w_1|+|w_2|$为例，其对应的权重集合在图像中表示为：

正则化不仅只有$L_1,L_2$正则化。在$\text{K-Means}$聚类算法中介绍过：

• $L_1$范数即权重与特征原点之间的曼哈顿距离($\text{Manhattan Distance}$)；
• $L_2$范数即权重与特征原点之间的欧几里得距离($\text{Euclidean Distance}$)。

它们都是明可夫斯基距离($\text{Minkowski Distance}$)的一种具体表示结果：
$$||\mathcal{W}|{|}_p={\left(\sum _{k=1}^m|w_k-0{|}^p\right)}^{\frac{1}{p}}$$
$m$不仅可以取$1,2$；它可以取到更大的数值，甚至是无穷大。对应图像举例表示如下：

观察，当参数$p\ge 1$时，满足$L_p$范数相等的点围成的集合图像是一个凸集合。而相反的， 0 < p ≤ 1 0

0<p≤1时，对应图像时一个非凸集合。而$L_1,L_2$正则化就合理利用了凸集特性，取处理神经网络中出现的过拟合问题。

正则化角度处理神经网络的过拟合问题

场景构建

• 具体针对某神经网络的输出层神经元进行描述。以多分类任务为例，对应选择的激活函数是$\text{Softmax}$函数：
  $$\{\begin{array}{l}{\mathcal{Z}}^{(l)}=[{\mathcal{W}}^{(l)}{]}^T\cdot a^{(l-1)}+b^{(l)}\\ a^{(l)}=\text{Softmax}({\mathcal{Z}}^{(l)})\end{array}$$
  其中${\mathcal{W}}^{(l)}$表示输出层神经元的权重；$a^{(l-1)}$表示上一层神经元的输入信息；${\mathcal{Z}}^{(l)}=({\mathcal{Z}}_1^{(l)},{\mathcal{Z}}_2^{(l)},\cdots ,{\mathcal{Z}}_p^{(l)}{)}_{p\times 1}^T$表示输出层对应线性运算结果。$a^{(l)}$表示输出层的最终输出。$\text{Softmax}({\mathcal{Z}}^{(l)})$展开结果表示如下：
  $$a^{(l)}=\text{Softmax}({\mathcal{Z}}^{(l)})={\left[\frac{\exp \{{\mathcal{Z}}_1^{(l)}\}}{{\sum }_{i=1}^p\exp \{{\mathcal{Z}}_i^{(l)}\}},\frac{\exp \{{\mathcal{Z}}_2^{(l)}\}}{{\sum }_{i=1}^p\exp \{{\mathcal{Z}}_i^{(l)}\}},\cdots ,\frac{\exp \{{\mathcal{Z}}_p^{(l)}\}}{{\sum }_{i=1}^p\exp \{{\mathcal{Z}}_i^{(l)}\}}\right]}_{p\times 1}^T$$
• 关于损失函数，这里使用极大似然估计($\text{Maximum Likelihood Estimate,MLE}$)
  $$\mathcal{J}(a^{(l)})=\text{MLE}(a^{(l)})$$

最优模型参数的不确定性

仅仅从输出层的角度观察该分类任务的目标：如果上一层的输出结果$a^{(l-1)}$确定的条件下，找到一组合适的权重、偏置${\hat{\mathcal{W}}}^{(l)},{\hat{b}}^{(l)}$使得损失函数达到最小：
$${\hat{\mathcal{W}}}^{(l)},{\hat{b}}^{(l)}=\underset{{\mathcal{W}}^{(l)},b^{(l)}}{\mathrm{argmax}}\mathcal{J}\left\{\text{Softmax}\left[({\hat{\mathcal{W}}}^{(l)}{)}^T\cdot a^{(l-1)}+{\hat{b}}^{(l)}\right]\right\}$$
但实际上，上一层的输出结果$a^{(l-1)}$并非是确定的，而对于$a^{(l-1)}$也同样受对应的${\mathcal{W}}^{(l-1)},b^{(l-1)}$约束。

• 假设通过$l-1$层的线性运算以及激活函数，使最终得到的输出结果${\hat{a}}^{(l-1)}=2\cdot a^{(l-1)}$：
  例如:使用$\text{ReLU}$激活函数，对应的${\mathcal{W}}^{(l-1)},b^{(l-1)}$均乘以$2$.
  $${\hat{a}}^{(l-1)}=2\cdot a^{(l-1)}=\text{ReLU}\left[2\cdot {\mathcal{W}}^{(l-1)}\cdot a^{(l-2)}+2\cdot b^{(l-1)}\right]$$
• 此时，由于$a^{(l-1)}\Rightarrow {\hat{a}}^{(l-1)}=2\cdot a^{(l-1)}$，在最终输出层中，同样需要调整输出层的参数来拟合最终结果：
  调整部分:${\hat{\mathcal{W}}}^{(l)}\Rightarrow \frac{1}{2}{\hat{\mathcal{W}}}^{(l)}$
  $${\mathcal{Z}}^{(l)}=\frac{1}{2}[{\hat{\mathcal{W}}}^{(l)}{]}^T\cdot \underset{{\hat{a}}^{(l-1)}}{2\cdot a^{(l-1)}}+{\hat{b}}^{(l)}$$

这里说明的是：在训练神经网络的过程中，假设能使损失函数达到最小的权重、偏置信息$\hat{\mathcal{W}},\hat{b}$不是唯一确定的。最终获取损失函数最小的$\hat{\mathcal{W}},\hat{b}$的大小取决于多种情况。例如：开始训练之前，对权重、偏置的初始化结果${\mathcal{W}}_{init},b_{init}$的大小。

随机初始化的${\mathcal{W}}_{init},b_{init}$虽然各不相同，并且可能差异极大，但并不影响该参数在反向传播过程中使得损失函数达到最小。也就是说，如果训练了若干次神经网络，并且都使损失函数达到了最小值，但每次训练产生的最终模型参数$\mathcal{W},b$可能是一组一组不同的值。

最优模型参数不确定性带来的问题

从理论上来说，我们仅需要观察损失函数达到最小对应的最优模型参数即可，但真实情况下，效果并非如此。

• 如果我们的数据集是一个全集：描述该任务中的所有样本均包含在数据集合中，即便参数不唯一，也不会影响最终的预测结果。

  在极大似然估计与最大后验概率估计中介绍过，在面对任务时，它对应的真实模型是客观存在的。也就是说，该真实模型可以源源不断地生成样本。因此，想要从真实模型中采样是永远采不完的。

  其次，如果真的得到一个全集，我们完全可以通过查询的方式得到对应结果。并且它是完全正确的。那就没有必要使用机器学习算法来解决该问题了。

• 同理，如果我们的预测任务仅仅在训练集中使用，参数不唯一同样不会影响最终预测结果。

  但机器学习的目的就是用来预测未知(训练集之外)的数据，这种做法与机器学习的目的相悖，没有使用意义。

假设在训练集经过若干次训练，得到了若干组各自之间存在差异的模型参数。这些模型参数有大有小，在对陌生数据使用模型进行预测时，不同大小参数计算得到对应的$\text{Softmax}$分量有大有小，最终可能导致分类存在差异的情况。

并且，样本自身存在噪声，也有可能存在 大的模型参数 和噪声之间的线性计算有可能主导了分类结果。使得最后判断的结果更容易出错。既然不同模型参数可能带来更多问题，我们是否可以寻找方法来约束一下参数$？$

约束模型参数的方法

针对上述问题，一种想法是约束模型参数的可行域范围：如果参数在可行域范围内，对于该参数的结果会认可；反之如果可行域范围之外，存在使得损失函数值更小的模型参数，也不会认可该参数。

关于可行域范围的描述，这里使用范数进行表示：

• 这里以$L_2$范数为例。
• 这里$\mathcal{J}$依然表示损失函数;$\mathcal{C}$表示可行域范围的常数,它表示权重空间中的点$\mathcal{W}$到原点之间的距离$\le \mathcal{C}$.
• 这里将$b$归纳进$\mathcal{W}$中，省略。
  $$\{\begin{array}{l}\min \mathcal{J}(\mathcal{W})\\ s.t.||\mathcal{W}|{|}_2-\mathcal{C}\le 0\end{array}$$

从图像角度观察

关于损失函数$\mathcal{J}$以及正则项$||\mathcal{W}|{|}_2-\mathcal{C}$对应在权重特征空间中的范围表示如下：

作为约束条件的正则项(绿色圆)，在圆内(包含边界)都是它的可行域范围；而褐色线表示损失函数的等高线，椭圆越小，它对应的权重的结果越优，损失函数越小。

为什么要选择蓝色点：实际上选择任意绿色圆内褐色线上的点都是满足约束要求的。但是只有蓝色点权重的向量分量对梯度下降方向的分量的比重最大。也可以理解成约束条件下的最优方向/权重。

从拉格朗日求解角度观察

这明显是一个带约束的优化问题。使用拉格朗日乘数法，对目标函数$\mathcal{L}(\mathcal{W},\lambda )$进行表示：
$$\mathcal{L}(\mathcal{W},\lambda )=\mathcal{J}(\mathcal{W})+\lambda (||\mathcal{W}|{|}_2-\mathcal{C})$$
由于是不等式约束，基于目标函数的优化结果可表示为：
其中$\lambda$表示‘拉格朗日乘子’。
$$\{\begin{array}{l}\underset{\mathcal{W}}{\min }\underset{\lambda }{\max }\mathcal{L}(\mathcal{W},\lambda )\\ s.t.\lambda \ge 0\end{array}$$
将目标函数$\mathcal{L}(\mathcal{W},\lambda )$展开，得到如下结果：
$$\{\begin{array}{l}\begin{array}{rl}\mathcal{L}(\mathcal{W},\lambda )& =\mathcal{J}(\mathcal{W})+\lambda (||\mathcal{W}|{|}_2-\mathcal{C})\\ & =\mathcal{J}(\mathcal{W})+\lambda ||\mathcal{W}|{|}_2-\lambda \cdot \mathcal{C}\end{array}\\ \mathcal{L}(\mathcal{W},\lambda )=\mathcal{J}(\mathcal{W})+\lambda ||\mathcal{W}|{|}_2\end{array}$$
其中上面的表示拉格朗日乘数法得到的结果；下面是常见的正则化表达结果。由于$\lambda ,\mathcal{C}$均是常数，对于求解最优权重$\mathcal{W}$不影响，从而有：
对两目标函数对$\mathcal{W}$求解梯度，由于常数$\lambda \cdot \mathcal{C}$的梯度是$0$,求出的$\mathcal{W}$最值自然是相同的。
$$\underset{\mathcal{W}}{\arg }\left(\begin{array}{c}\underset{\mathcal{W}}{\min }\underset{\lambda }{\max }\mathcal{J}(\mathcal{W})+\lambda ||\mathcal{W}|{|}_2-\lambda \cdot \mathcal{C}\\ s.t.\lambda \ge 0\end{array}\right)=\underset{\mathcal{W}}{\arg }\left(\begin{array}{c}\underset{\mathcal{W}}{\min }\underset{\lambda }{\max }\mathcal{J}(\mathcal{W})+\lambda ||\mathcal{W}|{|}_2\\ s.t.\lambda \ge 0\end{array}\right)$$
至此，关于正则化与拉格朗日乘数法得到的关于$\mathcal{W}$的优化解是等价的。

关于常数$\mathcal{C}$

关于$\mathcal{C}$的物理意义是：某权重点在权重空间中到原点的距离。就是上述绿色圆的半径。

但从上述正则化的角度观察，它并没有对常数$\mathcal{C}$进行约束，那么是否可以说明常数$\mathcal{C}$不重要呢？

自然不是。

在使用梯度下降法优化模型参数$\mathcal{W}$的过程中，每次迭代产生的梯度均与真正梯度结果大小相等，方向相反：
$${\mathcal{W}}^{(t+1)}\Leftarrow {\mathcal{W}}^{(t)}-\eta \cdot \frac{\partial \mathcal{L}({\mathcal{W}}^{(t)})}{\partial {\mathcal{W}}^{(t)}}$$
但是加入正则化后，我们的权重被约束在绿色圆范围内。而这个绿色圆的范围，也就是半径$\mathcal{C}$并不是一成不变的，而是需要达到一种微妙的平衡：

• 通过$L_2$范数的约束，使得学习出的权重尽量不出现过拟合；
• 被约束在绿色圆范围内，对应的权重预测结果是不够准确的，我们希望它更准确；

虽然我们没有直接约束$\mathcal{C}$，但是我们可以通过约束$\lambda$来约束绿色圆的范围。并且另一个重要原因是：调整$\lambda$，从而调整$\mathcal{C}$，最终实现蓝色点梯度与真正梯度大小相等。
如果每次迭代过程内，梯度的大小被确定的情况下，$\lambda \cdot \mathcal{C}$被约束在了一个确定的范围：

• 如果$\lambda$数值(人为设定)较大，这意味着$\mathcal{C}$较小，从而使权重可行域范围很小。这样的权重构建的模型预测结果必然不准确，从而使预测结果的偏差较大；
• 如果$\lambda$数值较小，着意味着$\mathcal{C}$较大。权重可行域范围更大。如果极端一点，该范围把损失函数的范围(褐色线)全覆盖上了，那么正则化没有意义，此时产生过拟合。最终会使预测结果的方差较大。
  这里有一道正则化与偏差方差的题，这里挖一个坑，后续介绍传送门

下一节将继续介绍正则化——从权重衰减的角度观察。

相关参考：
“L1和L2正则化”直观理解(之一)，从拉格朗日乘数法角度进行理解