STL sort 分析
前言
STL 中提供了很多算法,sort 是我们经常使用的,那它究竟是如何实现的呢?
STL 的 sort 算法,数据量大时采用快速排序,分段递归。一旦分段的数据量小于某个门槛,为避免快速排序的递归调用带来过大的额外负荷,就改用插入排序。如果递归层次过深,还用改用堆排序。这个算法接受两个随机迭代器,然后将区间内的所有元素以升序排列。第二个版本则允许用户指定一个彷函数作为排序标准,我们暂时不考虑这个版本。
注意本文并不教具体的排序算法,只是分析 sort 中的行为,对于插入排序和快速排序需自行掌握。
插入排序
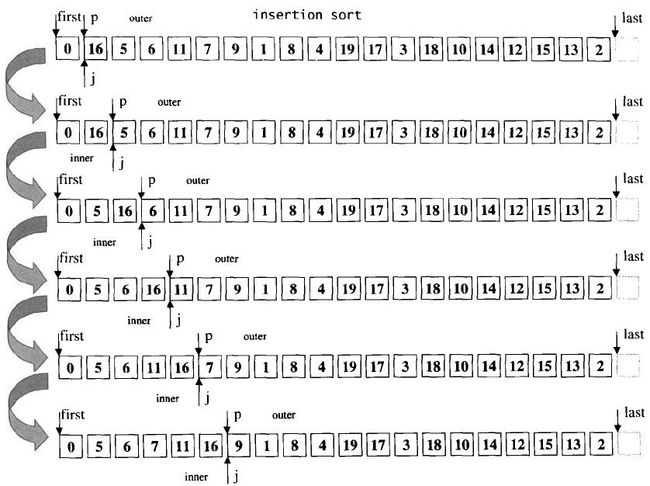
插入排序以双层循环的形式进行。外层循环遍历整个序列,每次迭代决定一个子区间;内循环遍历子区间,将当前值插入到合适的位置。
template <class RandomAccessIterator>
void __insertion_sort(RandomAccessIterator first, RandomAccessIterator last) {
if (first == last) {
return;
}
for (RandomAccessIterator i = first + 1; i != last; ++i) {
// 外循环,形成 [first, i) 的子区间
__linear_insert(first, i, value_type(first));
}
}
// 版本一辅助函数
template <class RandomAccessIterator, class T>
inline void __linear_insert(RandomAccessIterator first,
RandomAccessIterator last, T*) {
T value = *last; // 记录尾元素
if (value < *first) { // 尾比头还小
copy_backward(first, last, last + 1); // 令元素整体向后移动一个位置
*first = value; // 将尾元素插在头部
} else { // 尾不小于头
__unguarded_linear_insert(last, value);
}
}
// 版本一辅助函数
template <class RandomAccessIterator, class T>
void __unguarded_linear_insert(RandomAccessIterator last, T value) {
RandomAccessIterator next = last; // 指向尾元素
--next; // 调整指向前一元素
while (value < *next) { // 尾元素更小,插入位置应在前面
*last = *next; // 将 next 指向的元素值向后移动一个位置
last = next;
--next; // 向前移动迭代器,继续寻找
}
*last = value; // value >= *next 即为正确的插入位置
}
上面的代码看起来好像没什么特别之处,其实暗藏玄机。在一般的插入排序中,我们除了要判断两元素是否逆序外,还需要判断 next 是否超出了边届。
为什么上述代码不需要判断呢?
原因就在于上述代码的左边届一定是最小值,这在调用上一层 __linear_insert 时做的,该函数首先将要插入的值于左边届比较,更小就直接插入。此时,进入到 __unguarded_linear_insert 循环体的待插入值,一定大于等于左边届,就不可能出现越届的情况,也就可以把边届检查省略了。
快速排序
快速排序过程如下,假设 S 代表将被处理的序列:
- 如果 S 的元素个数为 0 或 1,结束
- 取 S 中的任何一个元素,当作枢轴 v
- 将 S 分隔为 L、R 两段,使 L 内的每一个元素都小于或等于 v,R 内的每一个元素都大于或等于 v
- 对 L,R 递归执行快速排序
快速排序的精神在于将大区间分割为小区间,分段排序。每一个小区间排序完成后,和起来的大区间也就完成了排序。
三点中值
理论上,任何一个元素都可以被选做枢轴,但合适与否却会影响快速排序的效率。比如一个已经升序的序列,我们每次都选其左端点作为枢轴,效率将退化为 O ( N 2 ) O(N^2) O(N2)。
最理想的方式是取整个序列的头、尾和中间三个位置的元素,以其中值作为枢轴。为了能够快速取出中央位置的元素,显然迭代器必须是随机迭代器。
template <class T>
inline const T& __median(const T& a, const T& b, const T& c) {
if (a < b) {
if (b < c) { // a < b < c
return b;
} else if (a < c) { // a < b,b >= c,a < c
return c;
} else { // a < b,a >= c
return a;
}
} else if (a < c) { // a >= b,a < c
return a;
} else if (b < c) { // a >= b,a >= c,b < c
return c;
} else { // a >= b,a >= c,b >= c
return b;
}
}
分隔
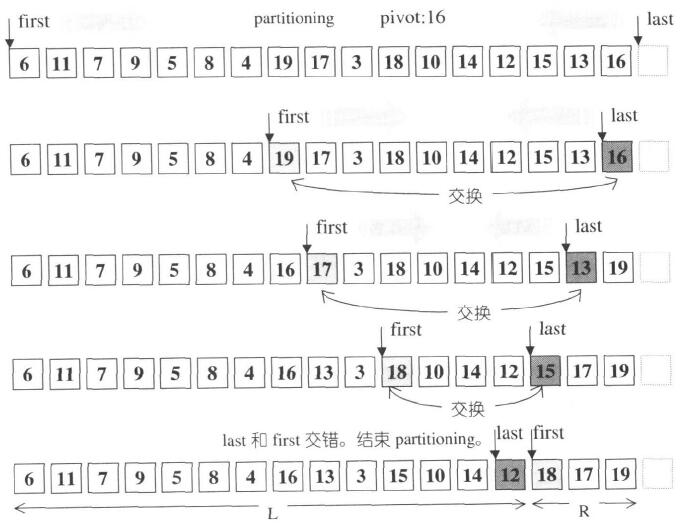
令头迭代器 first 向尾部移动,尾端迭代器 last 向头部移动。当 *first 大于或等于枢轴时就停下来,当 *last 小于或等于枢轴时也停下来,然后检验两个迭代器是否交错。如果 first 仍然在左,last 仍然在右,就将两者元素交换,然后各自调整一个位置。
下面是 SGI STL 提供的分隔函数,其返回值是分隔后右段第一个位置:
template <class RandomAccessIterator, class T>
RandomAccessIterator __unguarded_partition(RandomAccessIterator first,
RandomAccessIterator last,
T pivot) {
while (true) {
while (*first < pivot) { // 向后寻找大于等于枢轴的值
++first;
}
--last;
while (pivot < *last) { // 向前寻找小于等于枢轴的值
--last;
}
if (!(first < last)) { // first 在右,last 在左就退出
return first;
}
iter_swap(first, last);
++first;
}
}
阈值
面对一个数据量很小的序列,使用快速排序产生递归调用是不划算的。鉴于这种情况,适当评估序列的大小,然后决定采用快速排序或插入排序,是值得采纳的一种优化措施。不过对于多小的序列采用插入排序,暂时没有定论,5~20 都可能导致差不多的结果。
STL sort
下面是 SGI STL sort() 源代码:
template <class RandomAccessIterator>
inline void sort(RandomAccessIterator first, RandomAccessIterator last) {
if (first != last) {
__introsort_loop(first, last, value_type(first), __lg(last - first) * 2);
__final_insertion_sort(first, last);
}
}
__lg
__lg 是用来控制分隔恶化的情况:找出 2 k ≤ n 2^k \leq n 2k≤n 的最大值 k。
例:n = 10,得 k = 3;n = 2 得 k = 1;n = 20 得 k = 4。
template <class Size>
inline Size __lg(Size n) {
Size k;
// k 即为 n 最高位的 1 右边的位数
for (k = 0; n != 1; n >>= 1) {
++k;
}
return k;
}
__introsort_loop
当元素个数为 20 时,__introsort_loop() 的最后一个参数是 4 * 2,意思是最多允许分割 8 层。
template <class RandomAccessIterator, class T, class Size>
void __introsort_loop(RandomAccessIterator first,
RandomAccessIterator last, T*,
Size depth_limit) {
// __stl_threshold 是个全局常量,SGI STL 中定义为 16
while (last - first > __stl_threshold) {
if (depth_limit == 0) { // 分割恶化,改用堆排序
partial_sort(first, last, last);
return;
}
--depth_limit; // 分割一次就 --
// 枢轴通过 __median 获取
RandomAccessIterator cut = __unguarded_partition
(first, last, T(__median(*first, *(first + (last - first)/2),
*(last - 1))));
// 对右半段递归调用 __introsort_loop
__introsort_loop(cut, last, value_type(first), depth_limit);
// 调整边届,左半段在当前循环解决
last = cut;
}
}
上述代码中并没对左右两段递归调用,只是对右段递归调用,左半段调整边届后在循环内处理。这样的可读性较差,但可以减少一次递归调用的消耗。
__final_insertion_sort
如果我们令某个大小以下的序列停留的「接近排序但尚未完成」的状态,最后再用一次插入排序将所有这些「接近排序但尚未完成」的子序列做一次完整的排序,其效率一般认为会比「将所有子序列彻底排序」更好。这时因为插入排序在面对「接近排序」的序列时,有很好的表现。
template <class RandomAccessIterator>
void __final_insertion_sort(RandomAccessIterator first,
RandomAccessIterator last) {
if (last - first > __stl_threshold) { // 元素个数大于 16 个
__insertion_sort(first, first + __stl_threshold); // 保证最小元素在最左侧
__unguarded_insertion_sort(first + __stl_threshold, last); // 调用不用判断边届的插入排序
} else {
__insertion_sort(first, last);
}
}
上述代码非常奇怪,首先判断元素的个数。
为什么要这样做呢?
首先,快速排序是以 __stl_threshold 为最小阈值,也就是说最小值一定在最左边 __stl_threshold 个元素内。先将最小元素放在最左侧,再直接调用不用判断边届的插入排序,可以提高效率。否则,要先调用 __linear_insert,再与左端点值比较,再调用 __unguarded_insertion_sort。
template <class RandomAccessIterator>
inline void __unguarded_insertion_sort(RandomAccessIterator first,
RandomAccessIterator last) {
__unguarded_insertion_sort_aux(first, last, value_type(first));
}
template <class RandomAccessIterator, class T>
void __unguarded_insertion_sort_aux(RandomAccessIterator first,
RandomAccessIterator last, T*) {
for (RandomAccessIterator i = first; i != last; ++i) {
__unguarded_linear_insert(i, T(*i)); // 调用不用判断边届的插入排序
}
}