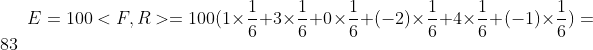【机器学习】EM原理和K-mean聚类
一、教程说明
EM算法就是expect maxmise算法，就是“期望最大化”的缩写。本篇首先提出：1 什么是期望？ 2 期望最大化是个啥意思？k-mean聚类中如何用EM算法？
所涉及的概念：
- 期望
- 期望的加权平均理解
- 概率模型和统计模型
- 期望最大化
- k-mean算法的原理
二、什么是期望？
2.1 从一个思想实验入门
在回答这个概念之前，我们可以做一个思想实验。
假如：我们这里有一枚六面骰子
1）每次掷出“1”奖励一块钱，那么掷出100次，您能得到几块钱？
我们很容易想到：掷出100次，获得“1”的次数大约100/6次,每次的1块，总数大约1×100/6 =16.6元。故
2）如果每次掷出“1”奖励一块钱，每掷出“2”奖励三元，那么掷出100次，您能得到几块钱？
100次掷出，得到“2”的可能次数为100/6， 每次奖励3块，那么总的收益数为：
3)更一般地，我们给出一个收益函数，那么，掷出100次后，总的收益是多少？
给出收益函数：
![F = [ 1, 3, 0,-2, 4,-1 ]](http://img.e-com-net.com/image/info8/fe0a8d2b8bea4cb29497e50acd28fd1f.gif){kind=small}
给出概率模型：
![R = [ 1/6, 1/6, 1/6, 1/6, 1/6, 1/6]](http://img.e-com-net.com/image/info8/a864a8f0886a4adea9ccdb2f5389c03a.gif){kind=small}
那么，抛掷100次后，总的收益就是期望，它的公式为：
E(F) =
- 掷出100次的获益（期望）：
- 掷出1 次的获益（期望）
结论：期望就是收益函数和概率模型的内积！此内积表示概率作用下的总收益。
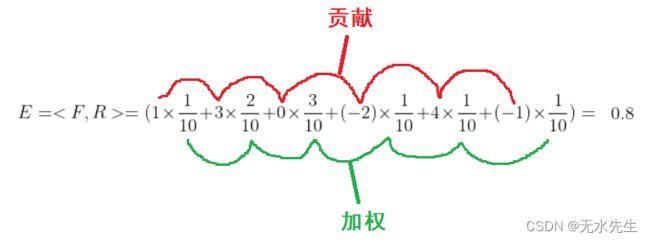
2.2 改变概率模型
将上面的概率模型是：将其改成其它模型：
![R = [ 0,1, 0.2, 0.1, 0.3, 0.1, 0.1, 0.1 ]](http://img.e-com-net.com/image/info8/49bbc13fdf11419cabe7cdeb24429da5.gif){kind=small}
期望可以如法炮制：
结论： 期望就是对“多路贡献”的加权平均。加权平均就是“多路贡献”的总贡献。
2.3 给期望一个定义
- 所谓期望，就是一个收益函数与一个概率分布模型的内积。
- 所谓期望就是在一个收益函数上施加概率模型，最终获益的总量。
- 所谓期望，就是一个收益函数，在一个概率模型下的收益的概率平均（或加权平均）。
注意：将收益函数赋予其它意义，期望还能有其它意义。
三、期望的几何意义
我们看这里是教材对期望的定义：
这个定义是否与上述的“收益函数”有矛盾？答曰“没有”，因为这里只要将“收益函数”定义为：
F = X 就可以了。问题是这种期望有啥意义？
期望的几何意义：一组数据的概率加权平均，或叫中心点，或叫重心。
四、期望的最大化原理（EM）
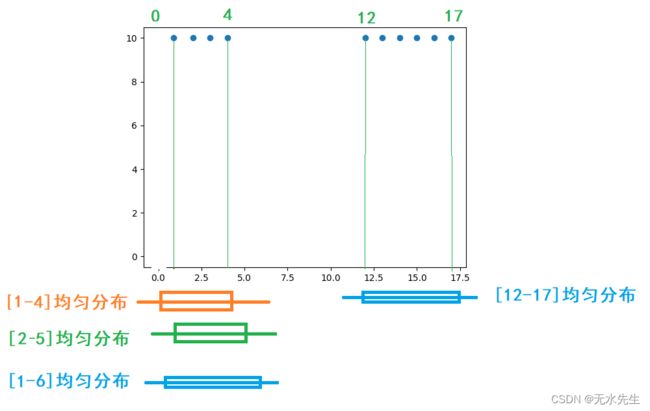
引理：如果一组数据符合统计规律，那么这组数据能和理论上的一个概率模型对应。
上图假定有两组数据，符合统计规律，且给出4个均匀分布概率模型。问两组数据分别和哪个理论模型匹配？
分别做内积：
组1和【1-4】期望： 【1，2，3，4】* 【1/4,1/4,1/4,1/4 】 = 2.5
组1和【2-5】期望： 【1，2，3，4，0】* 【0，1/4,1/4,1/4,1/4】 = 2.25
组1和【1-6】期望： 【1，2，3，4，0，0】* 【1/6，1/6,1/6,1/6,1/6,1/6】 = 1.666
因此：组1和【1-4】期望最大，说明组1和该分布最匹配。
组2和【12-17】的期望： 【12，13，14，15，16，17】* 【1/6，1/6,1/6,1/6,1/6,1/6】=14.5
结论：当一组数与一个概率模型匹配，那么它们的内积（期望）最大的。这就是期望最大原理。
五、K-mean算法原理
5.1 算法简要描述
kmeans的计算方法如下：
1 对于一组数据，我们假定需要将它们分成K 个类
2 随机选取k个中心点（期望）作为初始概率模型的位置（聚类重心）。
3 我们假设分类是合理的，遍历所有数据点，通过距离模型，将他们归到指定的概率模型中。
4 从以上的归类中，计算各分类的期望（平均值），修改聚类重心。并重新修改验证分类的合理性，并最近的中心点中。
5 重复3-4，直到这k个中心点不再变化（收敛了），或执行了足够多的迭代.
5.2 举个实际例子
给出如下数据集： Data = {2，3，4，10，11， 12，20，25，30 }
我们假定k=2（就是要分成两类）
随机给出两个点c1 = 9，c2=10，作为两个聚类中心（期望）
| 数据集（坐标） | 到c1距离 | 到c2距离 | 距离比较 | 最后归类 |
|---|---|---|---|---|
| 2 | 7 | 8 | < | c1 |
| 3 | 6 | 7 | < | c1 |
| 4 | 5 | 6 | < | c1 |
| 10 | 1 | 0 | > | c2 |
| 11 | 2 | 1 | > | c2 |
| 12 | 3 | 2 | > | c2 |
| 20 | 11 | 10 | > | c2 |
| 25 | 16 | 15 | > | c2 |
| 30 | 21 | 20 | > | c2 |
累计上表c1的数据平均 = （2+3+4 ）/3 = 3
累计上表c2的数据平均 = （10+11+12+20+25+30）/6 = 18
| 数据集（坐标） | 到c1距离 | 到c2距离 | 距离比较 | 最后归类 |
|---|---|---|---|---|
| 2 | 1 | 16 | < | c1 |
| 3 | 0 | 15 | < | c1 |
| 4 | 1 | 14 | < | c1 |
| 10 | 7 | 8 | < | c1 |
| 11 | 8 | 7 | > | c2 |
| 12 | 9 | 6 | > | c2 |
| 20 | 17 | 2 | > | c2 |
| 25 | 22 | 7 | > | c2 |
| 30 | 27 | 12 | > | c2 |
累计上表c1的数据平均 = （2+3+4+10）/4 = 4.75
累计上表c2的数据平均 = （11+12+20+25+30）/5 = 19.6
| 数据集（坐标） | 到c1距离 | 到c2距离 | 距离比较 | 最后归类 |
|---|---|---|---|---|
| 2 | 2.75 | 17.6 | < | c1 |
| 3 | 1.75 | 16.6 | < | c1 |
| 4 | 0.75 | 15.6 | < | c1 |
| 10 | 5.25 | 9.6 | < | c1 |
| 11 | 6.25 | 8.6 | < | c1 |
| 12 | 7.25 | 7.6 | < | c1 |
| 20 | 15.25 | 0.4 | > | c2 |
| 25 | 20.25 | 5.4 | > | c2 |
| 30 | 25.25 | 15.4 | > | c2 |
最后c1，c2无变化，算法停止，聚类结束！
六、概率模型和统计模型的关系
两者关系
- 不同点：概率模型从理论出发，描述数据。统计模型是从数据触发，获得理论参数。
- 共同点，两者都指向同一组数据，如果高度匹配，能使算法收敛。
七、代码实现
# -*- coding: utf-8 -*-
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import random
data = [
[ 0.697,0.46],[ 0.774,0.376],[ 0.634,0.264],[ 0.608,0.318],
[ 0.556,0.215],[ 0.403,0.237],[ 0.481,0.149],[ 0.437,0.211],
[ 0.666,0.091],[ 0.243,0.267],[ 0.245,0.057],[ 0.343,0.099],
[ 0.639,0.161],[ 0.657,0.198],[ 0.36,0.37],[ 0.593,0.042],
[ 0.719,0.103],[ 0.359,0.188],[ 0.339,0.241],[ 0.282,0.257],
[ 0.784,0.232],[ 0.714,0.346],[ 0.483,0.312],[ 0.478,0.437],
[ 0.525,0.369],[ 0.751,0.489],[ 0.532,0.472],[ 0.473,0.376],
[ 0.725,0.445],[ 0.446,0.459]]
# filepath = open('S:/机器学习-周志华/西瓜数据集4.0.csv')
# data = pd.read_csv(filepath, sep=',')[["密度", "含糖率"]].values.tolist() # tolist:ndarray转换为list
k = 3 # K值设置，3,4
mean_vectors = random.sample(data, k) # 初始化均值向量，随机K个
print(mean_vectors)
x0 = list(map(lambda arr: arr[0], mean_vectors))
y0 = list(map(lambda arr: arr[1], mean_vectors))
# 将初试的均值向量用红色的方块表示出
plt.scatter( x0, y0, c='r', marker=',' )
# 计算欧式距离
def Distance(p1, p2):
sum = 0
for i, j in zip(p1, p2):
sum = sum + (i - j) ** 2
return np.sqrt(sum)
time = 0 # 循环次数
clusters = [] # 聚类初始化
while time < 100: # 循环次数限制
clusters = list(map((lambda x: [x]), mean_vectors))
print(clusters)
change = 1
for sample in data:
dist = []
for j in mean_vectors:
dist.append(Distance(j, sample))
clusters[dist.index(min(dist))].append(sample)
new_mean_vectors = []
for c, v in zip(clusters, mean_vectors):
c_num = len(c)
c_array = np.array(c)
v_array = np.array(v)
new_mean_vector = sum(c_array) / c_num
# if all(np.divide((new_mean_vector - v), v) < np.array([0.0001, 0.0001])):
if all(np.true_divide((new_mean_vector - v_array), v_array) < np.array([0.0001, 0.0001])):
new_mean_vectors.append(v) # 不变
change = 0
else:
new_mean_vectors.append(new_mean_vector.tolist()) # 更新
if change == 1:
mean_vectors = new_mean_vectors
else:
break
time = time + 1
# Show the clustering result
x1 = list(map(lambda arr: arr[0], clusters[0]))
y1 = list(map(lambda arr: arr[1], clusters[0]))
x2 = list(map(lambda arr: arr[0], clusters[1]))
y2 = list(map(lambda arr: arr[1], clusters[1]))
x3 = list(map(lambda arr: arr[0], clusters[2]))
y3 = list(map(lambda arr: arr[1], clusters[2]))
# x4 = list(map(lambda arr: arr[0], clusters[3]))
# y4 = list(map(lambda arr: arr[1], clusters[3]))
# x5 = list(map(lambda arr: arr[0], clusters[4]))
# y5 = list(map(lambda arr: arr[1], clusters[4]))
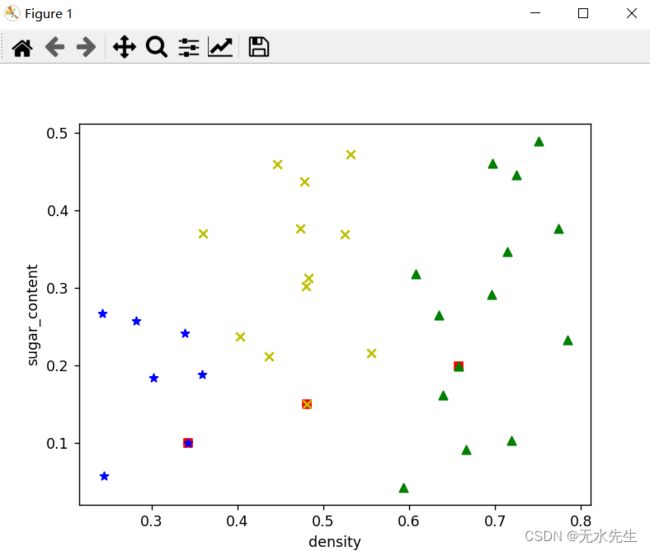
plt.scatter(x1, y1, c='y', marker='x', label='class1')
plt.scatter(x2, y2, c='g', marker='^', label='class2')
plt.scatter(x3, y3, c='blue', marker='*', label='class3')
# plt.scatter(x4, y4, c='black', marker='+', label='class4')
plt.xlabel('density')
plt.ylabel('sugar_content')
plt.show()
八、 总结
本讲从收益函数的期望入手，让大家直观理解“期望”就是收益函数的总和，这里注意，期望是两个函数的内积。
当将收益函数看成是数据的坐标，其几何意义就是数据中心位置。
加权平均是对期望的另外一个观点。
期望最大化，是指数据模型和某个概率分布的吻合度，越吻合，期望值越大。
概率模型和统计模型交互搭配，达到自动迭代运算，并用距离衡量其收敛性。