LeetCode高频题956：数组arr，能否把数组取出若干个数，使得取出数之和，与剩下数的和相同

LeetCode高频题956：广告牌问题：只包含正数的数组arr，能否把数组取出若干个数，使得取出数之和，与剩下数的和相同

提示：本题是系列LeetCode的150道高频题，你未来遇到的互联网大厂的笔试和面试考题，基本都是从这上面改编而来的题目
互联网大厂们在公司养了一大批ACM竞赛的大佬们，吃完饭就是设计考题，然后去考应聘人员，你要做的就是学基础树结构与算法，然后打通任督二脉，以应对波云诡谲的大厂笔试面试题！
你要是不扎实学习数据结构与算法，好好动手手撕代码，锻炼解题能力，你可能会在笔试面试过程中，连题目都看不懂！比如华为，字节啥的，足够让你读不懂题

---

题目

给定一个只包含正数的数组nums，请问能否把这个数组取出若干个数，使得取出的数之和，与剩下数的和相同。

数据范围：1<=n<=500

---

一、审题

输入：
第一昂一个正数n，表示数组nums的长度
第二行输入n个正数，表示arr的值

输出
如果满足条件，true，否则输出false

示例1
4
1 5 11 5
输出：true
1+5+5=11

示例2
4
1 2 3 5
输出：false
怎么着也无法搞定这个事

---

建议你看看LeetCode956：这个题目，是互联网大厂根据LeetCode956题目改编来的，那个题是广告牌问题，非常非常经典的算法原型：

你正在安装一个广告牌，并希望它高度最大。这块广告牌将有两个钢制支架，两边各一个。每个钢支架的高度必须相等。

你有一堆可以焊接在一起的钢筋 rods。举个例子，如果钢筋的长度为 1、2 和 3，则可以将它们焊接在一起形成长度为 6 的支架。

返回 广告牌的最大可能安装高度 。如果没法安装广告牌，请返回 0 。

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/tallest-billboard
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

示例 1：

输入：[1,2,3,6]
输出：6
解释：我们有两个不相交的子集 {1,2,3} 和 {6}，它们具有相同的和 sum = 6。
示例 2：

输入：[1,2,3,4,5,6]
输出：10
解释：我们有两个不相交的子集 {2,3,5} 和 {4,6}，它们具有相同的和 sum = 10。
示例 3：

输入：[1,2]
输出：0
解释：没法安装广告牌，所以返回 0。

提示：

0 <= rods.length <= 20
1 <= rods[i] <= 1000
sum(rods[i]) <= 5000

怎么样？
本题，是不是和LeetCode这个广告牌问题一模一样？？

就是同一个题，所以你很清楚，花联网大厂的题目怎么考了吧？就是改编LeetCode的经典题目，因此好好学习数据结构与算法，把LeetCode的高频题，搞清楚，这种题就能拿下。

---

笔试看看AC吗？排序o（nlog（n））之后，双指针搞定试试

笔试可能没那么多心思写最优解

既然nums是单调的

所以整个排序双指针试试
举个例子
arr= 1 5 11 5

（0）排序arr=1 5 5 11，L=0，R=N-1，然后让L滑动，默认ans=false
（1）当sumL （2）但是如果sumL>sumR,R–,说明右边过大了，需要补充R，回到（1）
（3）当L扩的累加和是=R，R–，L++，回到（1）标记
（4）如果L>=R，退出，此时如果sumL=sumR，ans=true

sumL=11,sumR=11，L越过R，而且左右和相同，OK

再举例：
1 2 3 5
最开始L不断扩，L=2也加上，sumL=6，因为大于sumR=5，R–
但是L>=R，退出，此时不相等左右和，false

手撕代码试试：

    //给定一个只包含正数的数组nums，请问能否把这个数组取出若干个数，使得取出的数之和，与剩下数的和相同。
    //
    //数据范围：1<=n<=500
    //输入：
    //第一昂一个正数n，表示数组nums的长度
    //第二行输入n个正数，表示arr的值
    //
    //输出
    //如果满足条件，true，否则输出false

    public static class Main {
        public static void main(String[] args) {
            Scanner in = new Scanner(System.in);
            // 注意 hasNext 和 hasNextLine 的区别
            int N = in.nextInt();//一个数字
            int[] arr = new int[N];
            for (int i = 0; i < N; i++) {
                arr[i] = in.nextInt();//一串数组
            }

            //排序双指针处理
            boolean ans = f(arr);
            System.out.println(ans);

        }

        public static boolean f(int[] arr){
            if (arr == null || arr.length == 0) return true;
            if (arr.length == 1) return false;

            int L = 0;
            int N = arr.length;
            int R = N - 1;
            int left = 0;
            int right = arr[N - 1];
            //（0）排序arr，L=0，R=N-1，然后让L滑动，默认ans=false
            Arrays.sort(arr);

            while (L < R){
                //（1）当sumL
                //（2）但是如果sumL>sumR,R--,说明右边过大了，需要补充R，回到（1）
                //（3）当L扩的累加和是=R，R--，L++，回到（1）标记

                if (left < right) left += arr[L++];
                else if (left > right) right += arr[--R];
                else {
                    left += arr[L++];
                    right += arr[--R];//同时操作
                }

            }
            //（4）如果L>=R，退出，此时如果sumL=sumR，ans=true
            return left == right;
        }
    }

测试一把：

6
1 5 5 6 7 10
true

问题不大：

4
1 2 3 5
false

看来排序双指针可以AC的

---

面试最优解：经典的算法原型：广告牌问题通吃互联网大厂改编的各种分组问题，o（n）复杂度一遍搞定

来，咱们用LeetCode956这个广告牌问题解决本题

说白了，就是让你找哪些数组能组合出左右相等的累加和？？？？
不妨设两个桶AB，咱们能就决定每一个数[i]究竟应该往哪个桶放？
如果放完arr，最后A累加和=B累计和
说明OK，否则不OK

下面开始，A就是A桶的累加和，B就是B桶的累加和

上面排序双指针，我们用了**o（nlog（n））**的复杂度搞，笔试当然可以AC，证明你的编程能力过关
但是面试，你用排序双指针，估计就得30分（100满分的话）

本题的最优解o（n）复杂度一遍搞定！！！

你当然很好奇，如何一遍看完arr，不排序还能搞定呢？？？？

老样子，你想速度快，就需要用额外空间换时间，没什么可说的

本题的思路很巧，准一个哈希表map
其key记录了AB两个桶的累加和之差，d=A-B
其value，记录的是造成这个累加和之差d的最小那个累加和，自然是A或者B，因为A-B=d
来一个arr的数，你就得决定放A,还是放B中，放完就会造成新的差d，然后更新map

比如：
arr=1 5 5 11
最开始map中记录了一个key=0，此时最小的累加和也是0，A,B没有数

请你决定1放哪里？
如果放A中，则A=1,B=0,则此时差值d=|A-B|=1，小累加和是B=0
map记录d和B

如果放B中，则A=0,B=1,则此时差值d=|A-B|=1，小累加和是A=0
map更新d=1这个小和，还是0不变

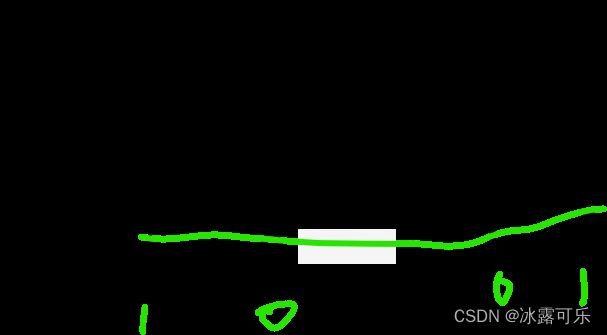
然后决定放5放哪个桶？

**注意，**你得在上一轮的基础上，决定放A还是B中
**注意，**你得在上一轮的基础上，决定放A还是B中
**注意，**你得在上一轮的基础上，决定放A还是B中

上一轮其实有两种情况：
A=1,B=0
A=0,B=1

假如在A=0,B=1的情况下放：
选择：放A，则A=5,B=1，差d=4，小和是B=1

选择：放B，则A=0,B=6，差d=6，小和是A=0

假如在A=1,B=0的情况下放：
选择：放A，则A=6,B=0，差d=6，小和是B=0
选择：放B，则A=1,B=5，差d=4，小和是B=1

……
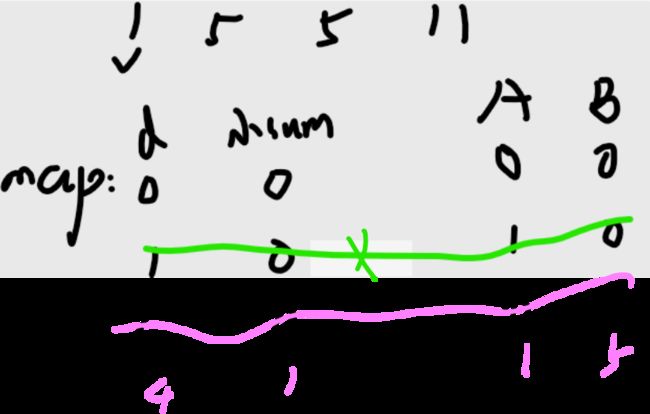
总之，你每次放arr[i]，都需要在上一轮的每种情况下去决定放A是一种方式，放B又是另一方式
反正你知道要怎么记录map了吧，就是放AB之差d，和小的那个累加和

为啥要记录这个map呢？

你看看，A-B=d，不管你arr[i]扔到哪个桶，都会出现一个差d

如果最后map中有d=0，但是value对应的不是0，而是一个具体的sum，你觉得是什么状况？？？？？

可不就是A-B=d=0，有A=B这个事出现【毕竟你的arri全部都决定丢在A,B中了，现在恰好均匀了】
那可不就是本题的答案true？

如果map中d=0这个key压根没有value>0，说明arr怎么放，都无法让AB累加和相同，也就无法造出一个AB左右平衡的sum来，导致这个value还是默认的0，返回false。

懂了吧，我为啥要记录这个AB差值d
而且，有了差d，小的那个累加和value【不妨设A是小的那个和】
那大的那个累加和可不就是B=A+d吗？
相当于每次，AB记录下来了，那我就可以方便去决定下一个数究竟放A,还是放B了。
总之，map记了A和AB之差d，我就可以通过A与d求出B来。
反之亦然

map就是干这个事的。

类似于排序双指针，**我们的想法就是，**我需要决定任意的arr[i]往哪里放，从而尽量让AB平衡
以期待A-B=d=0这种状况出现，这样本题就有true答案了。

代码怎么手撕呢？？？

其实就是上面的思想，每一次，在上一轮的所有可能的情况下，决定arr[i]放A，还是放B？？？
上一轮的所有情况怎么模拟呢？？？？
上一轮的所有情况，其实都放在map里面了，绝对美滋滋【因为我们说过了d和A，加起来就是B】，这些所有可能的AB中，你决定新来的[i]放A,还是放B，最终导致新的差值d出现，继续放map呗

明白？？
比如map之前有三个key，分别是d=0 1 4，他们对应的小和A是0 4 1
那自然d对应的大和B=d+A=0 5 5
也就是说AB组合上一轮的状况是：
0 0
4 5
1 5
现在你看看放新来的arri=6，去A，或者B
上一轮三种，都有可能是
分别在
0 0
4 5
1 5
中决定放A，还是放B？？
如果都放A，则新的A B是组合是
0+6=6 0，差为6
4+6=10 5，差为5
1+6=7 5，差为2
又重新更新map的key呗
如果都放B，则新的A B是组合是
0 0+6=6，差为6
4 5+6=11，差为7
1 5+6=11，差为10
又重新更新map的key呗

总之，你来到新的arr[i]，需要copy一份之前的map，把所有的情况，放一次A，放一次B
然后用新的组合更新map

最后arr都决定放完了，只要map中key=0对应的value>0就是true，否则就是false

广告牌问题要的结果，不是true或者false，它要最后能组合出A=B的A值

也就是你能否从arr中找到这么一组最大的A=B的左右均分的累加和，可能还有一个某个数，不能放进A,B，扔掉

比如1 1 5 5 11
有一个1需要扔掉，我们只能凑11=11出来，广告牌问题要的是11这个最大可能的钢管长度

       //广告牌问题最优解：
        //总之，你来到新的arr[i]，需要copy一份之前的map，把所有的情况，放一次A，放一次B
        //然后用新的组合更新map
        //
        //最后arr都决定放完了，只要map中key=0对应的value>0就是true，否则就是false

        public static int gAds(int[] arr){
            if (arr == null || arr.length == 0) return 0;
            if (arr.length < 2) return 0;

            HashMap<Integer, Integer> map = new HashMap<>(), cur;//key:A-B=d,value，min（A,B)
            //这种方式可以同时生成map和cur
            map.put(0, 0);//A=0,B=0,d=A-B=0默认的
            //你来到新的arr[i]，需要copy一份之前的map，把所有的情况，放一次A，放一次B
            //        //然后用新的组合更新map

            int N = arr.length;//至少2个元素以上
            for(int x : arr){
                if (x != 0){//0放AB都一样，改变不了结果
                    //上一轮的所有情：copy map
                    cur = new HashMap<>(map);//这就是重头戏，之前AB的所有组合，copy过来
                    for(int d : cur.keySet()){
                        //每一种d，决定了一种A B组合
                        int A = cur.get(d);//拿到A，恢复B

                        //然后决定新来的x放哪里？？
                        //如果放大的B中，没啥可说，A不动，但是B+d，d自然也就越来越大了
                        int dNew = d + x;//差值必然被拉大x
                        map.put(dNew, Math.max(A, map.getOrDefault(dNew, 0)));
                        //新差对应的小和，可能还是小的那个还是A，或者就是之前已经存在的那个dNew对应的累加和
                        //A和它比较，谁大就是谁，老大算了算，要是之前没有，就是不存在，A胜出

                        //如果放小的A中，则你需要看看A+x有没有干过此刻的B了
                        int B = d + A;;//先恢复现场，现在是考虑另一个情况，B就不能动了
                        A += x;//决定x放小的A中
                        dNew = Math.abs(A - B);//差值可能还是干不过d ，也可能逆转了导致A+x>B了
                        //如果A仍然<=B，则map的dNew记录A或者dNew原有的小和
                        if (A <= B) map.put(dNew, Math.max(A, map.getOrDefault(dNew, 0)));
                        //如果A逆转>B，则map的dNew记录B或者dNew原有的小和
                        else map.put(dNew, Math.max(B, map.getOrDefault(dNew, 0)));
                        //总之就是记录dnew和它对应的小和，看看谁更小就行--A,B都要放
                    }
                }
            }

            return map.get(0);//广告牌问题，可以舍弃某些数，让A=B就行了，返回A即可
        }
    }

测试：

System.out.println(gAds(arr));
4
1 5 5 11
11

LeetCode测试：


OK，通过

由广告牌问题改编到本题的手撕代码

我最开始为了讲清楚map的意思
距离说明map中key=0的value>0就算OK

其实不是的
就像广告牌问题中1 1 5 5 11【你全部都要的话，A可能是12 ，B=11，或者A=11,B=12，俩永远不会平衡的】
map的key=0放了11，其实是扔掉了1个1的
这种对于本题来说，其实是false，你说对吧？
【因为1 5 5 11才能搞出11= 11】

map其实是记录了所有可能的差值，不一定保证A=B ，map的0这个key，是记录了最大，最接近的A=B之差，因为你不断决定加入A,B过程中，差值0的AB一定是最大的左右俩桶。

那么我们需要咋搞呢？才能用这个结果呢？A=map.get(0)=B，到底本题要的结果，你A,B都用完了所有arr的数了吗？
其实很简单，你扔了了没有仍，就看arr整体的累加和sum是不是=2A

如果sum=2A，其实就是没扔，就是本题要的状况
如果sum!=2A，显然就是你扔了某些数，导致arr没有办法被均分给A=B

手撕代码：

        //广告牌问题最优解：改编到蔚来的题
        //总之，你来到新的arr[i]，需要copy一份之前的map，把所有的情况，放一次A，放一次B
        //然后用新的组合更新map
        //
        //最后arr都决定放完了，只要map中key=0对应的value>0就是true，否则就是false

        public static boolean g(int[] arr){
            if (arr == null || arr.length == 0) return true;
            if (arr.length < 2) return false;

            HashMap<Integer, Integer> map = new HashMap<>(), cur;//key:A-B=d,value，min（A,B)
            //这种方式可以同时生成map和cur
            map.put(0, 0);//A=0,B=0,d=A-B=0默认的
            //你来到新的arr[i]，需要copy一份之前的map，把所有的情况，放一次A，放一次B
            //        //然后用新的组合更新map

            int N = arr.length;//至少2个元素以上
            for(int x : arr){
                if (x != 0){//0放AB都一样，改变不了结果
                    //上一轮的所有情：copy map
                    cur = new HashMap<>(map);//这就是重头戏，之前AB的所有组合，copy过来
                    for(int d : cur.keySet()){
                        //每一种d，决定了一种A B组合
                        int A = cur.get(d);//拿到A，恢复B

                        //然后决定新来的x放哪里？？
                        //如果放大的B中，没啥可说，A不动，但是B+d，d自然也就越来越大了
                        int dNew = d + x;//差值必然被拉大x
                        map.put(dNew, Math.max(A, map.getOrDefault(dNew, 0)));
                        //新差对应的小和，可能还是小的那个还是A，或者就是之前已经存在的那个dNew对应的累加和
                        //A和它比较，谁大就是谁，老大算了算，要是之前没有，就是不存在，A胜出

                        //如果放小的A中，则你需要看看A+x有没有干过此刻的B了
                        int B = d + A;;//先恢复现场，现在是考虑另一个情况，B就不能动了
                        A += x;//决定x放小的A中
                        dNew = Math.abs(A - B);//差值可能还是干不过d ，也可能逆转了导致A+x>B了
                        //如果A仍然<=B，则map的dNew记录A或者dNew原有的小和
                        if (A <= B) map.put(dNew, Math.max(A, map.getOrDefault(dNew, 0)));
                            //如果A逆转>B，则map的dNew记录B或者dNew原有的小和
                        else map.put(dNew, Math.max(B, map.getOrDefault(dNew, 0)));
                        //总之就是记录dnew和它对应的小和，看看谁更小就行--A,B都要放
                    }
                }
            }

            //注意啊，这个map的key=0，可能记录了value>0，但是2*value竟然不是arr的累加和sum
            //那就是false
            int sum = 0;
            for (int i = 0; i < N; i++) {
                sum += arr[i];
            }

            return 2 * map.get(0) == sum;//2A=sum,就说明A=B，全部用了，这是蔚来的改编题要的答案
            //广告牌问题，只看最高高度，可以舍弃某一个数
        }

测试：

4
1 5 5 11
true

这样通过广告牌问题改变来的这个代码，就是咱们本题的核心
因此俩题目，是一模一样的

同样，将来如果面试笔试你遇到arr，最少要扔多少值
才能让A=B尽量平衡

这不就是让sum-2A吗？？？？

这就是经典的广告牌问题的改编，一串，太多了

据说本题还能优化为背包问题

arr累加和为sum
如果A=sum/2

你填一个dp[i][j]表，最开始默认dp都是-1
dp[i][j]代表从0–i范围内任意选arr元素，恰好能装j这么多和

如果最后你发现dp[M-1][A]!=-1,那很OK，一定是代表arr被均分了

这个代码你自己手撕，我就不写了。

---

总结

提示：重要经验：

1）本题，arr累加和为sum，如果A=sum/2，你填一个dp[i][j]表，最开始默认dp都是-1，dp[i][j]代表从0–i范围内任意选arr元素，恰好能装j这么多和，如果最后你发现dp[M-1][A]!=-1,那很OK，一定是代表arr被均分了
2）本题其实还可以通过排序双指针搞定，复杂度o(nlog(n))
3）本题还能直接通过改编LeetCode956题的广告牌问题来解决，让map记录所有AB桶可能的差值，最后map.get(0)=A，你看看2A是否为sum，是就true
3）笔试求AC，可以不考虑空间复杂度，但是面试既要考虑时间复杂度最优，也要考虑空间复杂度最优。