电源环路增益测试的原理与仿真（基于buck变换器和PID控制）

背景

DC-DC的其中一个测试项是环路稳定性（环路增益）。测试方式如下图：

• 在电源环路中串联入一个小电阻（图中的R5）
• 在电阻上施加一个微小的交流信号
• 测量电阻两端电压的幅值和相位
• 改变交流信号的频率，获得环路增益的幅频和相频曲线

之前一直有一些疑问：

• 在一个闭环系统中，为什么通过这种方式可以获得环路增益，最后测量的结果与环路增益是什么关系？
• 使用这种测量方式需要满足什么条件？

于是重新学习了《Fundamentals of Power Electronics》，理解环路增益测量的原理，并且搭建了一个仿真模型进行验证。同时也回顾了控制器的设计。

环路增益测量的原理

环路增益定义

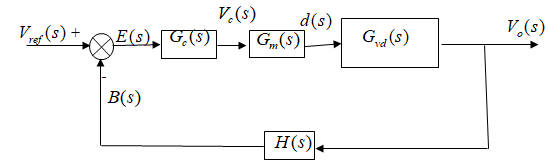
电源的闭环电压控制框图：

其中，Vg和iload是来自输入和负载的扰动，此处不考虑。

简化后的框图如下，有以下几个模块：

1. 变换器主电路Gvd(s)，输入为占空比d(s)，输出为输出电压Vo(s)
2. 反馈网络H(s)
3. 控制器Gc(s)
4. PWM调整模块，通常可等效为一个比例环节，Gm(s)=Km

再进一步简化成下图（G(s)=Gc(s)Gm(s)Gvd(s)），根据框图，有如下关系。

$$\begin{gathered} E(s)=R(s)-B(s) \\ C(s)=E(s)G(s) \\ B(s)=C(s)H(S) \\ \to \frac{C(s)}{R(s)}=\frac{G(s)}{1+G(s)H(s)}=\frac{1}{H(s)}\frac{G(s)H(s)}{1+G(s)H(s)}=\frac{1}{H(s)}\frac{T(s)}{1+T(s)} \end{gathered}$$

环路增益定义为T(s)=G(s)H(s)，是环路中所有环节的乘积。

• 当环路增益的幅值|T(S)|>>1时，有1+T(S)≈T(S)，因此C(s)/R(s)=1/H(s)，即输出仅与反馈系数H(s)有关。例如，集成DC-DC芯片，Rs对应芯片内部的电压基准，R(s)=0.6V，电阻分压决定反馈系数H(s)，如H(s)=10k/(10k+20k)=1/3，那么DC-DC的输出电压就是Vo=R(s)/H(s)=1.8 V

• T(s)的特性（增益、相位）影响负反馈系统的稳定性（具体原因需要参考奈奎斯特稳定性判据相关资料），具体如下图：

  1. 在|T(s)|=1时（0dB），T(s)的相位arg(T(s))需要大于-180°。相位裕量定义为180°-arg(T(sg))。
  2. 在arg(T(sp))=-180°时，T(s)的增益需要小于1（0dB）。增益裕量定义为0-20log(|T(sp)|)

  

有时候环路增益也被定义为-GH，因为环路中有一个参考量R与反馈量B相减的环节，把这个环节也考虑在内，就会引入-180°的相位。因此有些资料中的相位裕量是arg(T(s))与-360°的差，实际上两者是等效的。

测量方法

为了测量环路增益T(S)，需要在某个地方断开环路并接入测量设备。例如，在反馈环节G(s)中的某个点A和GND之间，如下图，把G(S)分为了两部分：

• 左侧根据误差信号Ve(s)调节占空比等，从而控制输出电压，通过戴维南等效为一个受控源和内阻Z1(s)
• 右侧通常是无源网络，等效为阻抗Z2(s)

基于上图，环路增益为：
$$T(S)=G_1(s)\frac{Z_2(s)}{Z_1(S)+Z_2(S)}{G}_2(s)H(s)$$

‘为了更直观地理解，以电压控制的buck电路为例，在反馈电阻处作为与GND之间作为A点，大致分为三部分，与上图对应：

• block1，包含PWM调制、反馈网络（PI控制器）、buck主电路，因此可以等效为受控源和内阻。
• block2，包含反馈用的分压电阻
• 计算反馈与参考的偏差（参考电压-反馈）

开环测量

注意：后续测量的电压的都是交流小信号，即去除直流偏置后的分量。

系统变为开环运行，给反馈网络加一个合适的偏置，使其达到与闭环运行时相同的工作点。

根据框图，测量结果为：
$$T_o=\frac{V_y(s)}{V_x(s)}=G_1(s)G_2(s)H(s)$$
测量值To(s)与实际值T(s)相比，少了Z2/(Z1+Z2)一项，因此，适用开环测量的条件是：|Z2|>>|Z1|。

对应到之前的buck电路，这种测量方式相当于：

• 断开反馈环路，并外接一个电源Vx作为控制器的输入
• 调节Vx的直流分量，使输出电压达到设定值
• 调节Vx的交流分量的频率，在各个频率下测量Vy和Vx，获得Vy/Vx的幅频和相频曲线

可以看到上图这种设置满足|Z2|>>|Z1|，因为Z1是电源的输出阻抗，显然远小于反馈网络的阻抗Z2。

开环测试的主要问题是，难以通过调节Vx使系统工作点与闭环情况相同。比如，在上图buck电路中，Vx电压分压后与参考电压的微小差异都可能使得后级PI控制器饱和，从而导致电路失控。并且工作点的偏移可能导致环路增益表现不同，测量结果不能反映实际情况。

因此，最好在闭环运行情况下测量环路增益。

电压注入法

较为常用的方法是电压注入法，如下图，在原A点位置串联一个交流源Vz，测量Vy/Vx。

$$\begin{gathered} i(s)=\frac{v_x(s)}{Z_2(s)} \\ -v_y(s)=-G_1(s)v_e(s)-i(s)Z_1(s)=-G_1(s)G_2(s)H(s)v_x(s)-i(s)Z_1(s) \\ \to T_v(s)=\frac{v_y(s)}{v_x(s)}=G_1(s)G_2(s)H(s)+\frac{Z_1(s)}{Z_2(s)} \end{gathered}$$
用理论Ts(s)表示：
$$T_v(s)=\frac{v_y(s)}{v_x(s)}=T(s)\left(1+\frac{Z_1(s)}{Z_2(s)}\right)+\frac{Z_1(s)}{Z_2(s)}$$

使用电压注入法，为了使测量值Tv(s)接近实际值T(s)，前提条件是：

• |Z2|>>|Z1|
• T(s)>>|Z1|/|Z2|

其中，若满足|Z2|>>|Z1|，则第二个条件T(s)>>|Z1|/|Z2|这个条件很容易满足。因此我们使用电压注入法时常说，

要求注入点的输出阻抗（Z1，从注入点往回看）远小于输入阻抗(Z2，从注入点往前看)

是主要因为：在输出与反馈电阻之间串联一个交流源Vz，测量Vy(s)=-Vo(s)和Vx(s)。

用电压注入法测量前文buck电路的环路增益，测量方式如下：在输出与反馈电阻之间串联一个交流源Vz，测量Vy(s)=-Vo(s)和Vx(s)。

电压注入法实现了在电源闭环运行的情况下测量环路增益。只要保证注入的交流电压幅值足够小，对系统的工作点基本无影响。

注入位置选择

理论上，注入位置可以是环路的任何一个点。但是，实际选择注入位置时需要关注输出阻抗<<输出阻抗的测试条件。环路测试仪Venable3120的说明书中给出了一些典型的注入位置。

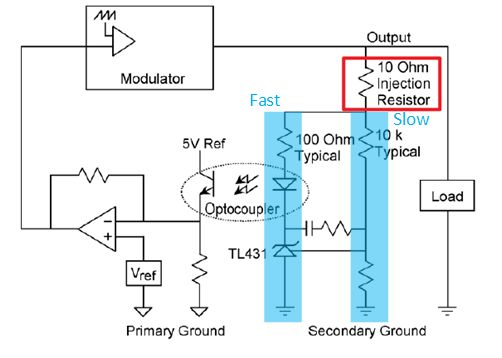
0. 对于基于TL431和光耦的反馈(常用于反激变换器等隔离型拓扑)，需要特别注意，注入的位置需要包括所有反馈路径（下图的Fast和Slow两条路径），而不是只注入其中某一条路径中。

   

1. 接在输出和反馈电阻之间（同上文buck电路的测量方式）

2. 接在控制器的输出

3. 接在控制器的负反馈路径中（但是可能会有较大噪声）

电流注入法

电流注入法与电压注入法原理类似，但是适用条件与电压注入法相反：

• |Z2|<<|Z1|
• T(s)>>|Z2|/|Z1|

环路增益测量的仿真分析

通过仿真帮助理解环路增益的测量方式。与理想模型对比，验证仿真结果的正确性。

仿真模型介绍

主电路

仿真软件使用LTspice。

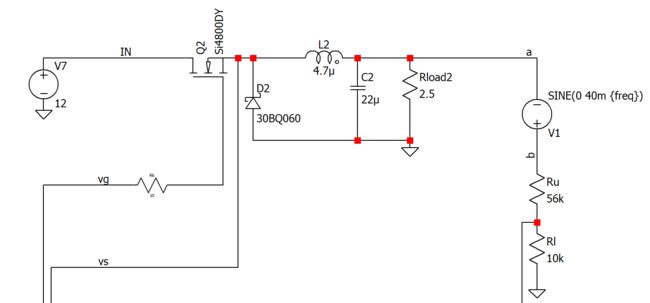
仿真模型为12V输入、5V2A输出的buck电路，开关频率固定在500kHz，LC等参数与常用的TPS562208等相同。V1用于电压注入，幅值根据需要调整，频率设置为freq。

根据最理想的模型和上图参数，buck电路的Gvd(s)的波特图如下，穿越频率在181/6.28=29kHz，可以适当提高一些，相位裕量8°，需要抬升。
$$G_{vd}(s)=\frac{V_i}{LC{s}^2+\frac{L}{R}s+1}$$

采样和控制

• 反馈电阻：选用常用的56k和10k组合，Vout=0.768*(1+56/10)=5.07V
• 控制器：下图是运放PI控制器，电压基准为0.768V。
• PWM调制：PI的输出与500kHz三角波比较，产生PWM波形
• MOS驱动：buck的高位MOS需要自举驱动，此处直接使用一个受控源来实现，驱动电压Vgs是运放输出电压的2倍，也就是高电平10V。

顺便一提，按照下图设置，输出采样电阻的上拉电阻Ru是补偿网络的一部分，但是下拉电阻Rl却不是。因为在小信号等效电路中，参考电压为0，根据运放虚短的特点，下拉电阻Rl和下图R12都接地，所以不影响环路，因此小信号下的反馈系数H=1。并联在上拉电阻两端的前馈电容会影响环路增益。

测量方式

理解LTspice中的环路增益测量方式，有助于理解实际环路测试仪的工作原理。主要原理：

• 在某个交流信号频率下，执行瞬态仿真
• 获取稳态的数据，计算幅值和相位
• 改变交流信号频率，重复测试

测量相关的指令需要直接放置在仿真模型中，如下图。

单次瞬态仿真

每次瞬态仿真对应注入交流信号的某一个频率。

具体指令如下：

• t0为仿真输出开始稳定的时刻，需要根据实际仿真情况设置
• 仿真运行时间为t0+25/freq，即稳定t0后再执行25个周期，只存储t0之后的稳态数据。

.param t0=1.2m
.tran 0 {t0+25/freq} {t0} 

处理单个频率点的数据

a点对应-Vy（根据之前的电压参考方向，实际上是-Vy），b点电压对应Vx。

在LTspice中，通过.measure来对波形数据进行一些运算。

计算某个频率下的Va/Vb的频率和相位：

• 首先，获得直流分量Aavg/Bavg，后续运算中减去直流分量，只使用交流小信号

• 通过离散傅里叶变换（DFT），分别获得实部和虚部，反映电压信号VA和Vb的幅值和相位。

• GainMag为增益20log(|Va|/|Vb|)

• GainPhi为相位裕量，举例如下：

  测量的相位是arg(Va(s)/Vb(s))=-300°，则实际T(s)相位是-120°，相位裕量为60°

  1. 因为实际测量的是Va/Vb=-Vy/Vx，所以此处先加上180度，还原为-Vy/Vx：-120°
  2. mod(x,360)：240°
  3. -180: 60°

.measure Aavg avg V(a)
.measure Bavg avg V(b)
.measure Are avg (V(a)-Aavg)*cos(360*time*Freq)
.measure Aim avg -(V(a)-Aavg)*sin(360*time*Freq)
.measure Bre avg (V(b)-Bavg)*cos(360*time*Freq)
.measure Bim avg -(V(b)-Bavg)*sin(360*time*Freq)
.measure GainMag param 20*log10(hypot(Are,Aim) / hypot(Bre,Bim))
.measure GainPhi param mod(atan2(Aim, Are) - atan2(Bim, Bre)+180,360)-180

DFT参考下式：实际只计算了所需的基频X[1]，忽略了其他分量。因为需要的是幅值的比值|Va|/|Vb|，仅需要相对大小，在此处具体幅值不重要。
$$X[k]=\sum _{n=0}^{N-1}{x}_n\cdot e^{-i2\pi kn/N}=\sum _{n=0}^{N-1}{x}_n[cos(2\pi kn/N)-i\cdot sin(2\pi kn/N)]$$

扫频

• 使用.step指令执行扫频，对freq范围内的多个取值，都分别执行一次瞬态仿真并存储数据，比如下面是5kHz~50kHz
• 使用.save指令存储关键的波形，比如V(a)和V(b)

.step oct param freq 5K 50K 5
.save V(a) V(b) V(out)  
.option plotwinsize=0 numdgt=15

测量环路增益Tv(s)

操作步骤

仿真模型搭建完成后，需要简单设置一下各项参数。

1. 需要确认Va和Vb的波形，要求没有明显畸变。因为是基于DFT处理获得幅度和相位，并且仅分析了Va和Vb基频分量，因此要求没有明显畸变，至少看起来像正弦波。

   例如，.step oct param freq 5K 50K 5会执行18次瞬态仿真，波形如下，符合要求。

2. 调整t0，.tran 0 {t0+25/freq} {t0} ，确认Va和Vb已达到稳态，例如下图。

3. 合理设置交流信号的幅值，使得从Va和Vb波形中能教准确地提取出基频分量。例如下图，从波形上看，交流信号的幅值大于开关频率的纹波。

所有仿真运行完成后，幅值和相位数据存储在仿真文件所在目录下的xx.log文本文件中。可以复制Freq、GainMag和GainPhi数据，用其他软件绘制波特图，也可以通过以下步骤在LTspice中绘制波特图：

1. View-SPICE Error log

2. 在log中右键，Plot .step'ed .meas data画图

3. 选择是，作为复数绘制

   

4. 弹出窗口中，右键，view-visible traces，选择gain，获得环路增益Tv(s)的波特图，如下。其中相位的读数已经是相位裕量，比如下图中，穿越频率约38kHz，相位裕量7.9°。

使用PI控制器

使用的PI控制器和使用的参数如下（此处的参数根据仿真结果调试得到，参数过大会导致输出振荡），可以看到电压采样电阻R1也影响控制器参数：
$$G_{PI}(s)=\frac{R_2}{R_1}+\frac{1}{R_1{C}_{1}s}=2+\frac{1786}{s}$$

使用PI控制器，理论和仿真测量的环路增益Tv(s)波特图如下，

• 幅频特性，除了谐振峰值有差异外，其他部分基本一致，穿越频率约37kHz。差异的主要原因是仿真模型考虑了寄生参数，而理论波特图假设所有元件都是理想的。
• 相频特性，有10°左右的偏差，但是总体趋势是一致的，相位裕量理论8°，仿真17°，相位裕量都不足。因为PI控制器不能抬升相位，下图已经是相位裕量较好的情况了。

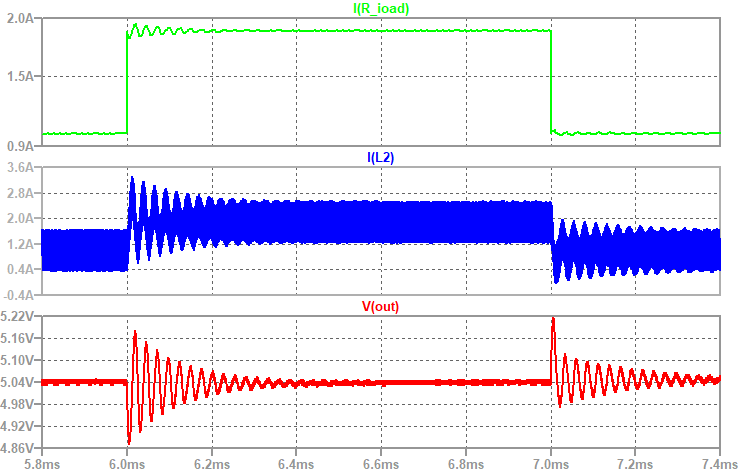
测试半载到满载切换的暂态波形，可以看到负载电流跳变后，输出电压有振荡，且需要较长时间（500 us）才能稳定。

使用PID控制器

PID控制器和参数如下。此处参数是按照目标穿越频率50kHz（1/10开关频率）设计。为了便于选择参数，采样处加了一级电压跟随器E1，彻底消除了采样电阻的影响。
$$G_{PID}(s)=\frac{(1+C_2{R}_{2}s)(1+C_1{R}_{1}s)}{C_2{R}_{1}s(1+C_1{R}_{3}s)}$$

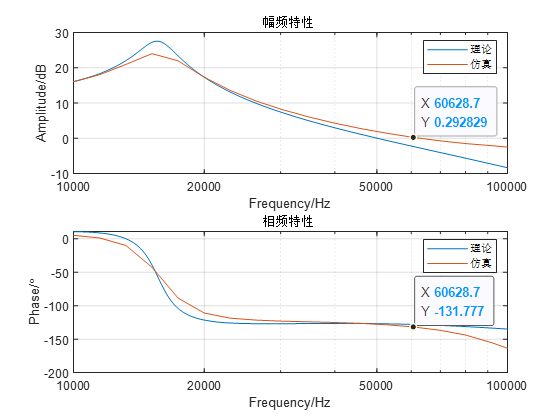
使用PID控制器，理论和仿真测量的环路增益Tv(s)波特图如下，

• 幅频特性，可以看到理论选择的穿越频率正好是50kHz，但是仿真达到了60kHz，有一定差异。可能原因是实际仿真的寄生参数、控制器选择的RC参数有偏差。
• 相频特性，也有约10°的偏差，但是趋势一致。相位裕量约49°，满足要求。

同样测试半载到满载切换的暂态波形，可以看到负载电流跳变后，输出电压的过冲幅值小于使用PI控制器的情况，并且仅需要70us左右就可以达到稳态。

总结

• 介绍了环路增益的定义、测量原理和稳定性判断方法
• 电压注入法要求注入点输出阻抗<<输入阻抗，需要合理选择测量位置
• 通过LTspice仿真，进一步说明了环路增益的测试方法。基于buck电路，对比了使用PI和PID两种控制器测量得到的环路增益和动态性能。