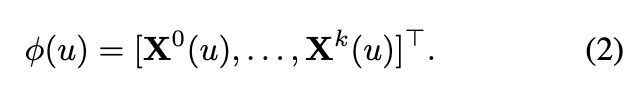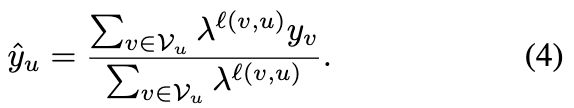论文阅读-Subgraph Centralization: A Necessary Step for Graph Anomaly Detection

论文链接：https://arxiv.org/pdf/2301.06794.pdf

 代码链接：Codes/IDK/GraphAnomalyDetection at main · IsolationKernel/Codes · GitHub

目录

摘要

1 简介

2 相关工作

3 节点异常：定义

3.1 基于h子图的节点异常

4 拟议框架：GCAD

4.1 子图提取和集中化（SEC）

4.2 子图嵌入

4.3 点异常检测器

 4.4 基于深度的加权分数

 5 将中心化应用于两个检测器

5.1 集中化一个基于子图的检测器——CoLA

5.2 集中基于全图的检测器——OCGNN

6 实验设计和结果

6.1主要评估

6.2 可解释性

6.3 参数 h 对 GCAD 的影响

 6.4 放大测试和时间复杂度

---

摘要

        图异常检测最近引起了很多兴趣。

        前人方法缺陷：尽管取得了成功，但现有检测器至少存在三个弱点中的两个：(a) 高计算成本，这将它们仅限于小规模网络； (b) 子图的现有处理产生次优的检测精度； (c) 无法解释节点异常的原因，一旦它被识别。

        gap: 我们发现这些弱点的根本原因是缺乏对子图的适当处理。

        提出了一种称为子图集中化的图异常检测处理方法来解决上述所有弱点。它的重要性体现在两个方面。

        首先，我们提出了一个简单而有效的新框架，称为以图为中心的异常检测 (GCAD)。

        优势：与包括深度学习检测器在内的现有检测器相比，GCAD 的主要优势是：(i) 更好的异常检测精度； (ii) 相对于节点数量的线性时间复杂度； (iii) 它是一个通用框架，允许使用现有的点异常检测器来检测网络中的节点异常。其次，我们表明可以将子图集中化合并到两个现有检测器中以克服上述弱点。

1 简介

        背景：

        属性网络在各种应用中无处不在，因为它们是表示节点信息以及节点之间关系的强大手段。

        例子是：（a）在社交网络[15]（例如，Facebook，博客，LinkedIn）中，具有跟随或被其他用户跟随的属性信息的用户可以被视为属性网络中的节点和连接；

        (b)在科学出版物的引用网络[7]中，作者表示节点，节点之间的连接表示作者之间的联合发表。

        属性网络中的异常节点检测有很多应用，例如欺诈检测、社交垃圾邮件检测和学术不端行为检测。

        前人方法：

        现有的异常节点检测器可以分为两种方法，即基于全图的检测器和基于子图的检测器。前者计算成本高，仅限于小型网络。我们发现后者没有充分发挥子图的潜力，导致检测精度不佳。此外，一旦节点被识别，这两种类型的检测器都无法解释节点异常的原因。

        子图的重要性可以从以下事实来理解：每个节点 v 都受到在以 v 为中心的子图中直接和传递地连接到它的所有节点的影响。子图外的通过许多跳连接的节点可以忽略不计或没有影响。因此，子图之间的的相似性决定了子图是正常的还是异常的。

        前人方法局限性：

        尽管现有的第二种方法具有相同的理解，但该方法有一个严重的弱点，即在计算子图之间的相似性之前没有执行中心化。因此，子图之间的相似性可能会产生误导。图 1(a) 中显示了一个示例：子图 G(v1) 被认为更类似于 G(v3)，而不相似于G(v2)，因为前两个图的节点位置更接近，即在相似度计算中，节点位置比图结构起着更重要的作用。

 （图 1：(a) 给定节点向量空间中（未显示）网络的三个示例子图。红色节点表示子图 G(v) 的源节点 v。 M 表示子图之间的相似性度量。 (b) 在平移空间中，每个集中子图 G'(v) 的所有节点都平移到与源节点 v 平移到原点相同的程度。 G′(v1) = G′(v2) 因为它们具有相同的结构。）

        直观上，子图之间的相似性主要依赖于图结构，给定节点向量在空间中的绝对位置在计算中不起作用。这可以通过将子图G(v) 的所有节点平移到与源节点v被平移到原点相同的程度来实现。图 1(b) 显示了图 1(a)（在原始空间中）所示子图的平移子图（在平移空间中）。事实上，平移后的子图 G'(v1) 和 G'(v2) 之间的相似性是统一的，因为它们具有相同的结构；由于结构的不同，它们中的每一个都与 G'(v3) 不太相似。

        我们称这种技术为子图集中化。我们表明，这是提出的新图异常检测框架和解决现有检测器的所有上述弱点的必要步骤。

        我们的主要贡献总结如下：

        通常定义网络中的正常和异常节点。据我们所知，我们是第一个在图异常检测方面提供此类定义的。

        提出一个简单但有效的新框架，称为 Graph-Centric Anomaly Detection 或 GCAD，它采用 Subgraph Centralization 作为必要步骤。 GCAD 能够检测大规模网络上的异常，并提供节点异常/正常的解释。该框架还允许使用现有的点异常检测器来执行图异常检测。

        证明子图集中化可以应用于两个现有的检测器，以提高它们的检测精度，并增强它们解释预测的能力。

        GCAD 不同于现有的两种方法，具有两个独特的特征，即使用集中子图作为相似性测量和可解释性的基础。子图是节点异常定义和GCAD框架设计的关键。集中化很简单，但对 GCAD 的成功至关重要。GCAD的可解释性依赖于集中子图，但与GCAD中使用的点异常检测器无关。

2 相关工作

        为了检测异常，对代表网络正常性的网络的某些特征进行建模至关重要。

        我们将现有工作分为两种方法，即在建模中使用整个网络还是子图：基于全图的方法是从整个网络中对某种形式的正常特征进行建模。

全图建模

        ANOMALOUS [16] 根据网络结构选择特征空间上的属性，并应用残差分析来检测异常。

         DOMINANT [5] 将 GCN [10] 与自动编码器结合起来重建网络（通过属性矩阵和邻接矩阵），使得正常节点的重建误差很小。

        其他一些作品 [6, 11] 也遵循了相同的方法并做了一些改进。

        Oddball [1] 通过幂律模型对网络的正常特征进行建模。

        OCGNN [22] 应用 GCN 和超球面学习 [18] 在网络上执行表示学习。

子图建模

        基于子图的方法利用各种方法从网络中提取子图。

        CoLA [14] 生成大量正负子图，其中正态子图描述了网络中每个节点与其相邻结构之间的正态关系；而负子图则没有。该集合用于训练分类器。

         ANEMONE [8] 和 SL-GAD [26] 通过生成围绕目标节点的子图并执行补丁级别和上下文级别的对比学习来采用自我监督学习。然而，它们都没有使用子图中心化，导致我们在第 1 节中提到的问题。

3 节点异常：定义

        令 G = {V, E, X } 为无向属性网络，其中 V = {v1, . . . ，vn}表示节点集合，E表示边集合，X∈Rn×d表示节点的属性矩阵，每个节点向量有d个属性。

        节点异常检测定义为：

        定义 1（节点异常检测） 网络 G = {V, E, X } 中节点异常检测的任务是识别网络中少数具有不同于大多数节点特征的节点异常，并根据异常评分对所有节点进行排名，使节点异常排名高于正常节点；

        要实施上述通用定义，必须设计一种方法为每个节点提供分数。

        我们建议在下一小节中使用h子图作为基本方法。

3.1 基于h子图的节点异常

        定义 2（h-子图） 一个 h-子图 是以源节点 v 为根的子图，使得 中任意节点与 v 之间的最短路径的长度≤ h , 其中 h ∈ N 是子图的最大深度。

        给定一个网络 G = {V, E, X } 有 n 个节点，总共有 n 个 h-子图。在n个h-子图中，那些数量少且在某种程度上与大多数h-子图不同的被认为是异常的；并且这些h-子图的源节点被视为G中的节点异常。我们建议使用相似性度量来表征h-子图之间的差异。

        基于h子图的节点异常定义如下。设节点集 V 由两个子集  和 组成，分别表示异常节点集和正常节点集，其中 , 和 M (·,·) 是两个 h-子图之间的相似性度量.

        定义 3 G = {V, E, X } 中的节点 u 是:

异常节点定义：

        如果 与大多数其他 h- 子图相似，即 很大，则为正常节点。

         • 如果 Gh(u) 与大多数其他 h-子图不同，即 很小，则为异常节点。

        在实践中，差异可以参数化为：如果 ，则 u 是异常节点。 否则u是一个普通节点。或者简单地选择具有最低相似度的前 m 个异常节点。 

4 拟议框架：GCAD

        我们提出了一个名为 GCAD（以图形为中心的节点异常检测）的新框架来检测网络中的节点异常。

整体架构概述：

        GCAD 通过检查从网络中提取的 h 子图之间的相似性对每个节点进行评分。如果以 v 作为源节点的 h-子图与网络中的大多数其他 h-子图不同，则节点 v 具有高分。

        所提出的框架由四个主要部分组成：子图提取和集中化、子图嵌入、异常检测和子图基于深度的加权异常评分，如算法 1 所示。由于基本操作单元是 h-子图，因此算法开始从由 n 个节点组成的给定网络中提取 n 个 h-子图。        

         为了实现 h 子图之间的相似性测量，一个关键步骤是集中所有这些 h 子图以消除节点向量空间中节点位置的不必要干扰，因为我们对它们在节点向量空间中的绝对差异不感兴趣。只有这样，纯粹基于单个 h 子图的结构来检查 h 子图之间的（不）相似性才有意义。这个过程是子图集中化。提取和集中化都在算法 1) 的第 1 行中进行。

        然后，需要一种嵌入方法来为每个 h 子图生成嵌入表示（算法 1 中的第 3 行）。然后可以将现有的点异常检测器应用于嵌入向量集，以检测与集合中的大多数不同的节点异常，如算法 1 中的第 6 行所示。由于每个 h 子图都来自源节点，每个h子图的异常分数表示其源节点的异常分数。

        最后，为了得出节点 u 的最终分数（算法 1 中的第 6 行），使用加权异常评分方法聚合包含节点 u 的所有 h-子图的源节点的异常分数。我们在以下四个小节中提供了四个步骤的详细信息。

4.1 子图提取和集中化（SEC）

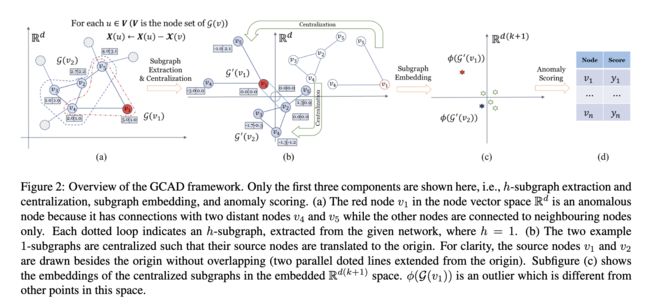
        图 2a 提供了子图提取过程的说明。给定 h 设置，从给定网络中提取 h 子图很简单：网络中的每个节点都被视为源节点 u；源节点 u 的 h 子图通过连接节点提取到深度 h。两个 1-子图位于图 2b 的右上角。

 (GCAD 框架概述。这里仅显示前三个组件，即 h-子图提取和集中、子图嵌入和异常评分。 (a) 节点向量空间  中的红色节点 v1 是异常节点，因为它与两个远距离节点 v4 和 v5 有连接，而其他节点仅与相邻节点连接。每个虚线循环表示从给定网络中提取的 h-子图，其中 h = 1。(b) 两个示例 1-子图是集中化的，因此它们的源节点被转换为原点。为清楚起见，源节点 v1 和 v2 在原点旁边绘制，没有重叠（从原点延伸的两条平行虚线）。子图 (c) 显示了嵌入 空间中集中子图的嵌入。 是一个异常值，不同于该空间中的其他点。)

        根据定义 3，目的是比较各个 h-子图的结构，这些 h-子图由 h-子图中节点的相对位置确定，但与节点向量空间中节点的绝对位置无关。

平移节点：

        为了实现这一目标，子图集中化组件将h-子图的所有源节点映射到节点向量空间的原点。为了确保每个 h 子图的结构保持不变，h 子图中的每个节点都被平移到与其源节点平移到原点相同的程度。这种集中化消除了节点向量空间中原始位置的不必要干扰，并且只允许比较 h 子图的结构。该过程如图 2b 所示。上述两个过程的详细过程如算法 2 所示。

         一旦上述过程完成，大多数彼此相似的集中式h-子图就构成了网络中的正常h-子图。少数与正常子图不同的集中式 h 子图是异常。为了便于进行这样的比较，我们需要将每个 h-子图嵌入到一个向量中，这是下一小节的主题。为了简洁起见，我们使用 来表示一个中心化的 h-子图，其中源节点为 v.

4.2 子图嵌入

        子图嵌入方法 φ 将每个集中的 h-子图 映射到向量 φ()。我们使用广泛使用的子图嵌入方法，Weisfeiler-Lehman (WL) [20, 25]。更具体地说，对于每个 h-子图  = {V, E, X}，我们利用节点向量空间中的 WL 方案来获得 h-子图每个节点的嵌入。关键思想是创建一个显式传播方案，该方案通过对邻域中的节点向量进行平均来利用和迭代更新当前节点向量。

         令每个节点 u ∈ V 的节点向量 。对于 k ≥ 1，第 k 次迭代的节点向量  通过 WL 计算如下： ​​​​

         其中 deg(u) 表示节点 u 的度数，N(u) 是 h-子图  中节点 u 的一跳邻居的集合。

        定义 4 h-子图中节点 u 的 WL 嵌入向量  = {V, E, X} 定义为 φ(u) ∈ ： 

         请注意，每次迭代的嵌入连接与其他基于 GNN 的方法不同，因为基于 GNN 的嵌入不会连接不同层的输出。

        定义5 整个h-子图的WL-嵌入向量定义为h-子图中所有节点的平均嵌入：

        因为 h-子图的最大 k 是 h。因此，我们设 k = h。

4.3 点异常检测器

         给定一组嵌入向量，然后可以使用现有的无监督异常检测器来检测与集合中的大多数不同的异常。令 E 为嵌入向量  的矩阵。

        我们假设 Detector(E) 从 E 开始训练并产生输出 Y，它是网络中所有节点 v 的异常分数  的一维矩阵。任何现有的点异常检测器都可以在这里使用。

 4.4 基于深度的加权分数

        最后一小节中的点异常检测器为节点 v 生成一个分数 ，节点 v 是给定网络中每个节点的 h-子图  的源节点。该分数可以直接作为每个节点的异常分数。但是，我们在这里引入了基于深度的加权分数以进一步改进。

         设 u 是感兴趣的节点， 是包含 u 的 h- 子图的所有源节点的集合。基于深度的加权得分聚合了  中所有 h- 子图的得分。这个想法是把一个更大的权重(小于1)放在 的分数  上，如果 u 更接近 v。

         权重使用参数 λ 表示为 ，其中 0 ≤ λ < 1； 是  中从 v 到 u 的跳数。        

        节点 u 的最终异常分数  定义为：

 5 将中心化应用于两个检测器

        在这里，我们表明子图集中适用于现有的基于子图的检测器 CoLA [14] 和现有的基于全图的检测器 OCGNN [22]。它们将在接下来的两小节中进行描述。

5.1 集中化一个基于子图的检测器——CoLA

        Contrastive self-supervised Learning framework for Anomaly detection on attributed networks (CoLA) [14] 是最近最先进的图形异常检测，它使用子图的对比学习来学习分类器，以便它可用于生成每个节点的异常分数。我们在下面展示了我们的子图集中化可以很容易地插入 CoLA 中，通过在学习分类器之前对 CoLA 的子图执行子图集中化来提高其检测准确性。具体来说，如图 3 所示，名为 CoLA SC 的新版本采用三个步骤来获取集中化子图。

 （CoLA SC 在从网络中采样子图后执行子图集中化。红色节点表示本例中的目标节点。）

        具体来说，如图 3 所示，名为 CoLA SC 的新版本采用三个步骤来获取集中子图。第一步是以随机顺序遍历每个节点作为每个时期内的目标节点。然后，对于给定的目标节点，通过重启随机游走（RWR）[21] 对正子图和负子图进行采样。正子图是从目标节点生成的；并且负子图来自与目标节点不同的节点。前两步与[14]中的方式相同。在第三步中，正负子图都按照算法2中的方式集中。在获得集中子图后，使用完全相同的训练步骤来学习CoLA检测器。详细信息可以在 [14] 中找到。

5.2 集中基于全图的检测器——OCGNN

        一级图神经网络 (OCGNN) [22] 集成了 GNN 和一级超球面学习以提供端到端检测器。具有 Subgraph Centralization 的增强版本称为 OCGNN SC。附加功能如下所示。在训练端到端检测器之前，使用随机游走 [21] 为每个节点生成子图，然后将每个子图集中到节点向量空间的原点，如前所述。采用平均池函数作为 GNN 的读出函数，然后进行与 OCGNN 相同的超球面学习。

6 实验设计和结果

        实验旨在回答以下问题：

        i. Subgraph Centralization 是图异常检测问题的必要步骤吗？

        ii. Subgraph Centralization 如何获得其可解释性？为了回答第一个问题，我们使用以下基线方法：

        Oddball [1] 是专门设计用于检测具有 clique 和 star 的节点异常类型的检测器。它学习网络的幂律模型来表示正常邻域，并​​计算每个节点与模型期望值的偏差作为异常分数。

        DOMINANT [5] 是一种基于 GCN-Autoencoder 的方法，表示为 DOM。它应用两个解码器来重建属性和邻接矩阵。异常分数是通过将两个重建误差与权衡系数相结合来计算的。

        CoLA [14] 是一种对比学习方法，它训练基于 GCN 的模型来区分网络中的节点异常和正常节点

        OCGNN [22] 是一种利用 GCN [10] 和超球面学习 [18] 来检测异常的方法异常。

        在 GCAD  中，我们使用最近的隔离分布内核 [19]（简称 IDK）作为算法 1 中第 6 行的点异常检测器。我们还在稍后的消融研究中检查了替代的现有无监督异常检测器。其他实验设置在附录中给出。

        第 6.1 节报告了第一个问题的调查。第二个问题的答案在第 6.2 节中给出。在以下两个小节中报告了两个额外的实验，它们检查 h 在 h 子图中的影响和放大测试

6.1主要评估

        该评估使用两组数据集，即合成数据集和现有数据集。它们的数据特征如表2所示，现简要说明如下。合成数据集。我们使用四种经典图生成模型 [9、23、4、3] 创建了六个合成数据集。

        对于 RGG 和 Lattice，我们创建了两种类型的数据集，一种中的正常节点是另一种中的异常节点。这样的设置可以帮助我们评估方法在检测不同于真实数据集中发现的异常类型的不同类型异常方面的能力（详见附件）。与之前的工作一样，假设原始引文网络数据集，即 Cora、Citeseer、Pubmed 和 ACM 没有异常，并注入了两种类型的异常。它们与 [14] 中使用的相同。

        总体结果。表 2 的观察结果是：

        • GCAD 是最好的。它在十个数据集中的七个中表现最好，在其他三个例外中表现第二。在 p = 0.01 的显着性水平上，它也明显优于其他六个竞争者中的每一个。唯一的例外是采用集中化的 CoLA SC

        子图集中化显著提高了CoLA和OCGNN的性能，接近GCAD的水平。在几乎所有数据集上，OCGNN的改进都是巨大的。类似地，对CoLA的改进是在所有有改进空间的数据集上，尽管改进的程度较小。

 （不同方法的 AUC 检测精度。 ‘Orig’表示原始方法； “SC”表示使用子图集中化修改的方法。最后一行显示了与 GCAD 相比从成对显着性检验获得的 p 值。倒数第二行显示了每种方法的排名，平均所有数据集。）

6.2 可解释性

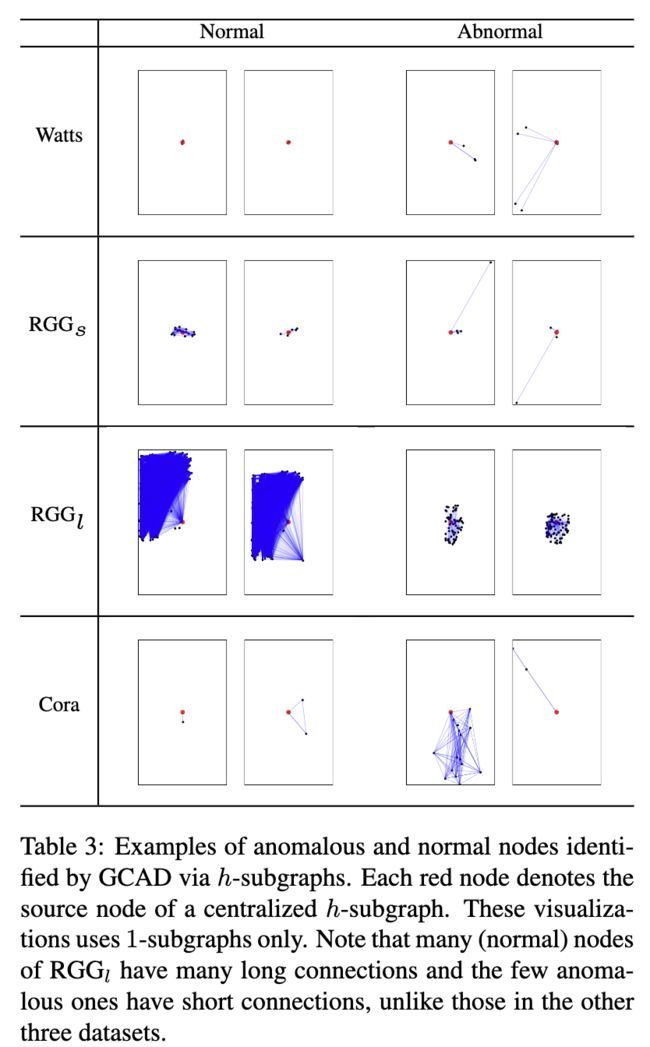
        表 3 显示了 GCAD 通过 h 子图识别的异常和正常节点的示例。这种通过可视化的解释是可能的，因为在异常检测之前使用了 Subgraph Centralization。前两个正常 h 子图表示网络中存在的典型 h 子图（在排名列表中排名底部）。

 （GCAD 通过 h 子图识别的异常和正常节点的示例。每个红色节点表示集中式 h 子图的源节点。这些可视化仅使用 1 个子图。请注意，RGGl 的许多（正常）节点具有许多长连接，而少数异常节点具有短连接，这与其他三个数据集中的节点不同。）

        前两个异常 h 子图表示网络中最不寻常的 h 子图。表 3 中的示例表明，检测到的异常的 h 子图与每个数据集中的正常 h 子图显着不同。有趣的是，这种可解释性仅取决于集中子图的使用，并且独立于算法 1 中第 6 行中使用的点异常检测器。因为现有的三个检测器，即 CoLA、DOMINANT 和 OCGNN 都没有使用子图集中化对于检测，他们无法提供这样的可视化来解释他们的检测结果。然而，在使用 Subgraph Centralization 之后，CoLA SC 和 OCGNN SC 具有相同的可解释性。

6.3 参数 h 对 GCAD 的影响

        当 h = 1 时，GCAD 在十分之九的数据集中表现最好，唯一的例外是 RGG。这意味着最简单的 1-子图足以检测几乎所有数据集上的异常。附录中的图 6 显示了 h 对不同数据集的影响。

 6.4 放大测试和时间复杂度

        图 4 显示了 GCAD、DOMINANT 和 CoLA 在 Watts-Strogatz 上的扩展测试结果，其中节点数从 103 增加到 106。

        为了公平比较，我们测量了每个算法在相同环境下所花费的时间。结果表明，GCAD 需要的计算量要少得多，并且可以处理大规模的百万节点网络。 DOMINANT 和 CoLA 在应用于百万节点网络时花费了非常长的时间。 GCAD 不同组件的时间复杂度在表 4 中给出。GCAD 具有线性时间复杂度，因为  和其他参数是常数。请注意，CoLA 和 OCGNN 的时间复杂度不包括深度学习时间。