Frechet distance距离计算原理及python实现
Frechet distance概念
弗雷彻距离(Frechet distance)定义了一种考虑位置和点的次序的计算两条曲线相似度的方法,常用于时间序列相似度度量和轨迹序列相似度度量。该指标的算法可用the walking dog problem来描述:想象一个人用牵引带遛狗的同时,穿过一条有限弯曲的路径,而狗则穿过一条单独的有限弯曲路径。每个人都可以改变自己的速度来放松牵引带,但都不能向后移动。则两条路径之间的Fréchet距离是牵引带的最短长度,足以让两条弯路从头到尾穿过各自的路径。
严格的数学定义为:
曲线A,B为度量空间S内的两条曲线,即 A : [ 0 , 1 ] → S A:[0,1]\rightarrow S A:[0,1]→S, B : [ 0 , 1 ] → S B:[0,1]\rightarrow S B:[0,1]→S。 α \alpha α和 β \beta β是单位区间的两个重采样函数, α : [ 0 , 1 ] → [ 0 , 1 ] \alpha:[0,1]\rightarrow [0,1] α:[0,1]→[0,1]。弗雷彻距离为: F ( A , B ) = inf α , β max t ∈ [ 0 , 1 ] ( d ( A ( α ( t ) ) , B ( β ( t ) ) ) ) F(A,B)=\inf_{\alpha,\beta}\max_{t\in[0,1]}(d(A(\alpha(t)),B(\beta(t)))) F(A,B)=α,βinft∈[0,1]max(d(A(α(t)),B(β(t))))
通俗的数学定义可以简化为:
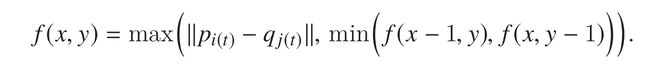
代码实现
基于动态规划,求两条轨迹的弗雷彻距离,具体的,将轨迹A和B每步分为三类可能的路径状态,1)A和B都向前移动一步;2)A停留原地,B向前移动一步;3)A向前移动一步,B停留原地;
import numpy as np
from scipy.spatial import distance
from scipy.spatial import minkowski_distance
from scipy.spatial.distance import euclidean
import seaborn as sns
def Frechet_distance(exp_data,num_data):
"""
cal fs by dynamic programming
:param exp_data: array_like, (M,N) shape represents (data points, dimensions)
:param num_data: array_like, (M,N) shape represents (data points, dimensions)
# e.g. P = [[2,1] , [3,1], [4,2], [5,1]]
# Q = [[2,0] , [3,0], [4,0]]
:return:
"""
P=exp_data
Q=num_data
p_length = len(P)
q_length = len(Q)
distance_matrix = np.ones((p_length, q_length)) * -1
# fill the first value with the distance between
# the first two points in P and Q
distance_matrix[0, 0] = euclidean(P[0], Q[0])
# load the first column and first row with distances (memorize)
for i in range(1, p_length):
distance_matrix[i, 0] = max(distance_matrix[i - 1, 0], euclidean(P[i], Q[0]))
for j in range(1, q_length):
distance_matrix[0, j] = max(distance_matrix[0, j - 1], euclidean(P[0], Q[j]))
for i in range(1, p_length):
for j in range(1, q_length):
distance_matrix[i, j] = max(
min(distance_matrix[i - 1, j], distance_matrix[i, j - 1], distance_matrix[i - 1, j - 1]),
euclidean(P[i], Q[j]))
# distance_matrix[p_length - 1, q_length - 1]
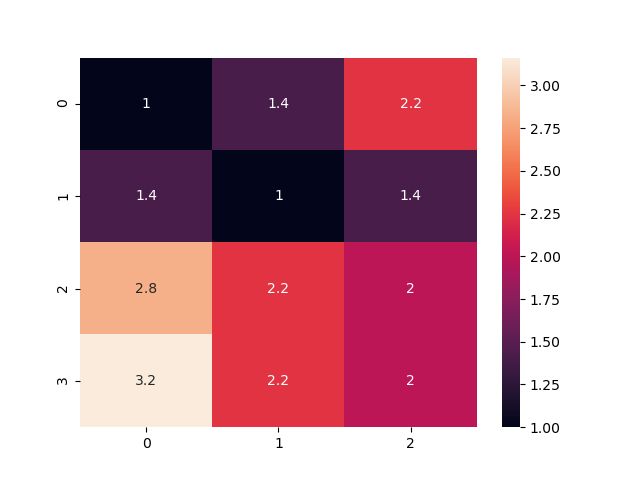
sns.heatmap(distance_matrix, annot=True)
return distance_matrix[p_length-1,q_length-1] # 最后一步即为弗雷彻距离
参考资料
[1] Thomas Eiter and Heikki Mannila. Computing discrete Frechet distance. Technical report, 1994. http://www.kr.tuwien.ac.at/staff/eiter/et-archive/cdtr9464.pdf http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.90.937&rep=rep1&type=pdf
[2] similarity_measures python package
[3] https://en.wikipedia.org/wiki/Fr%C3%A9chet_distance
[4] 通俗的数学描述及动态规划求解