C++ 红黑树
红黑树
- 红黑树
-
- 红黑树的性质
- 红黑树的结构
- 红黑树的插入
-
- 情况1
- 情况2
- 情况三
- 实现代码
- 红黑树模拟实现STL中的map/set
-
- 迭代器
- 改造红黑树
- map
- set
- list
红黑树
红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可以是Red或Black通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路径会比其他路径长出俩倍,因而是接近平衡的。
通过颜色互斥来控制平衡
近似平衡,最长路径最多是最短路径的二倍
红黑树的性质
- 每个结点不是红色就是黑色
- 根节点是黑色的
- 如果一个节点是红色的,则它的两个孩子结点是黑色的(没有连续的红色结点)
- 对于每个结点,从该结点到其所有后代叶结点的简单路径上,均包含相同数目的黑色结点-》每条路径上都包含相同数量的黑色结点
- 每个叶子结点都是黑色的(此处的叶子结点指的是空结点)
最短路径:全部由黑色结点构成
最长路径:一黑一红,红色结点数量跟黑色结点数量相等
思考:为什么满足上面的性质,红黑树就能保证:其最长路径中节点个数不会超过最短路径节点个数的两
倍?
红黑树的结构
为了后续实现关联式容器简单,红黑树的实现中增加一个头结点,因为跟节点必须为黑色,为了与根节点进行区分,将头结点给成黑色,并且让头结点的pParent域指向红黑树的根节点,pLeft域指向红黑树中最小的节点,_pRight域指向红黑树中最大的节点
红黑树的插入
因为新节点的默认颜色是红色,因此:如果其parent节点的颜色是黑色,没有违反红黑树任何性质,则不需要调整;但当新插入节点的parenet节点颜色为红色时,就违反了性质三不能有连在一起的红色节点,
cur为当前节点,p->parent,g->grandfather,u->uncle
情况1
cur为红,p为红,g为黑,u存在且为红
注意:此时所看到的树,可能也是子树


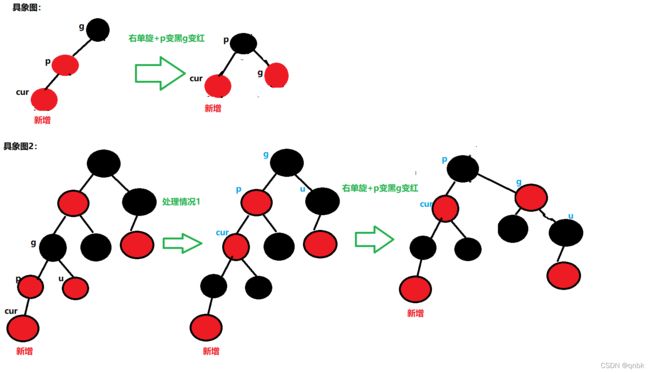
情况2
cur为红,p为红,g为黑,u不存在/u存在且为黑
说明:
u的情况有两种
- 1、如果u结点不存在,则cur一定是新插入结点,因为如果cur不是新插入结点,则cur和p一定有一个结点的颜色是黑色,不满足性质4:每条路径黑色结点相同
- 2、如果u结点存在,则其一定是黑色的,那么cur结点原来的颜色一定是黑色的,现在看到是红色是因为cur在子树调整的过程中将cur结点的颜色由黑色改成红色
p为g的左孩子,cur为p的左孩子,则进行右单旋转;
相反,p为g的右孩子,cur为p的右孩子,则进行左单旋转
p、g变色–p变黑,g变红

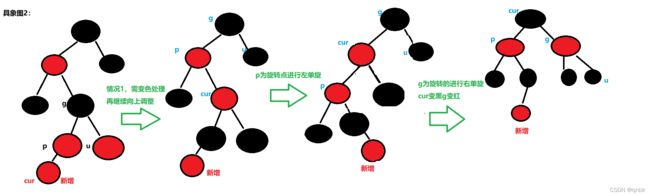
情况三
cur为红,p为红,g为黑,u不存在/u为黑
p为g的左孩子,cur为p的右孩子,则针对p做左单旋转;
相反,p为g的右孩子,cur为p的左孩子,则针对p做右单旋转,则转换成了情况2

实现代码
(没封装版)
#pragma once
#include 红黑树模拟实现STL中的map/set
迭代器
#pragma once
// 反向迭代器--迭代器适配器
template<class Iterator>
struct ReverseIterator
{
typedef typename Iterator::reference Ref;
typedef typename Iterator::pointer Ptr;
typedef ReverseIterator<Iterator> Self;
Iterator _it;
ReverseIterator(Iterator it)
:_it(it)
{}
Ref operator*()
{
return *_it;
}
Ptr operator->()
{
return _it.operator->();
}
Self& operator++()
{
--_it;
return *this;
}
Self& operator--()
{
++_it;
rteurn *this;
}
bool operator!=(const Self& s) const
{
return _it != s._it;
}
bool operator==(const Self& s) const
{
return _it == s._it;
}
};
改造红黑树
#pragma once
#include _kv.second<_right);
}*/
/*void InOrder()
{
_InOrder(_root);
cout << endl;
}
*/
private:
Node* _root;
};
map
#pragma once
#include "RBT2.h"
namespace rbt{
template<class K, class V>
class map
{
struct MapKeyOfT
{
const K& operator()(const pair<const K, V>& kv)
{
return kv.first;
}
};
public:
typedef typename RBTree<K, pair<const K, V>, MapKeyOfT>::iterator iterator;
typedef typename RBTree<K, pair<const K, V>, MapKeyOfT>::reverse_iterator reverse_iterator;
reverse_iterator rbegin()
{
return _t.rbegin();
}
reverse_iterator rend()
{
return _t.rend();
}
iterator begin()
{
return _t.begin();
}
iterator end()
{
return _t.end();
}
pair<iterator, bool> insert(const pair<const K, V>& kv)
{
return _t.Insert(kv);
}
V& operator[](const K& key)
{
pair<iterator, bool> ret = insert(make_pair(key, V()));
return ret.first->second;
}
private:
RBTree<K, pair<const K, V>, MapKeyOfT> _t;
};
}
set
#pragma once
#include "RBT2.h"
namespace rbt
{
template<class K>
class Set
{
struct SetKeyOfT
{
const K& operator()(const K& key)
{
return key;
}
};
public:
typedef typename RBTree<K, K, SetKeyOfT>::iterator iterator;
typedef typename RBTree<K, K, SetKeyOfT>::reverse_iterator reverse_iterator;
reverse_iterator rbegin()
{
return _t.rbegin();
}
reverse_iterator rend()
{
return _t.rend();
}
iterator begin()
{
return _t.begin();
}
iterator end()
{
return _t.end();
}
pair<iterator, bool> insert(const K& k)
{
return _t.Insert(k);
}
private:
RBTree<K, K, SetKeyOfT> _t;
};
}
list
#pragma once
#include iterator;
// typedef _list_iterartor const_iterator;
template<class T, class Ref, class Ptr>
struct _list_iterartor
{
typedef Ref reference;
typedef Ptr pointer;
typedef _list_node<T> node;
typedef _list_iterartor<T, Ref, Ptr> self;
node* _pnode;
_list_iterartor(node* pnode)
:_pnode(pnode)
{}
// 拷贝构造、operator=、析构我们不写,编译器默认生成就可以用
// T& operator*() iterator 可读可写
// const T& operator*() const_iterator 可读可写
Ref operator*()
{
return _pnode->_val;
}
Ptr operator->()
{
return &_pnode->_val;
}
bool operator!=(const self& s) const
{
return _pnode != s._pnode;
}
bool operator==(const self& s) const
{
return _pnode == s._pnode;
}
// ++it -> it.operator++(&it)
self& operator++()
{
_pnode = _pnode->_next;
return *this;
}
// it++ -> it.operator++(&it, 0)
self operator++(int)
{
self tmp(*this);
_pnode = _pnode->_next;
return tmp;
}
self& operator--()
{
_pnode = _pnode->_prev;
return *this;
}
self operator--(int)
{
self tmp(*this);
_pnode = _pnode->_prev;
return tmp;
}
};
template<class T>
class list
{
typedef _list_node<T> node;
public:
typedef _list_iterartor<T, T&, T*> iterator;
typedef _list_iterartor<T, const T&, const T*> const_iterator;
typedef ReverseIterator<iterator> reverse_iterator;
reverse_iterator rbegin()
{
return reverse_iterator(iterator(_head->_prev));
}
reverse_iterator rend()
{
return reverse_iterator(iterator(_head));
}
iterator begin()
{
return iterator(_head->_next);
}
const_iterator begin() const
{
return const_iterator(_head->_next);
}
iterator end()
{
return iterator(_head);
}
const_iterator end() const
{
return const_iterator(_head);
}
list()
{
//_head = new node(T());
_head = new node;
_head->_next = _head;
_head->_prev = _head;
}
// copy(lt)
list(const list<T>& lt)
{
_head = new node;
_head->_next = _head;
_head->_prev = _head;
for (const auto& e : lt)
{
push_back(e);
}
}
//copy = lt1;
/* list& operator=(const list& lt)
{
if (this != <)
{
clear();
for (const auto& e : lt)
{
push_back(e);
}
}
return *this;
}*/
// copy = lt1;
list<T>& operator=(list<T> lt)
{
swap(_head, lt._head);
return *this;
}
~list()
{
clear();
delete _head;
_head = nullptr;
}
void clear()
{
iterator it = begin();
while (it != end())
{
//it = erase(it);
erase(it++);
}
}
void push_back(const T& x)
{
insert(end(), x);
}
void push_front(const T& x)
{
insert(begin(), x);
}
void pop_back()
{
erase(--end());
}
void pop_front()
{
erase(begin());
}
void insert(iterator pos, const T& x)
{
assert(pos._pnode);
node* cur = pos._pnode;
node* prev = cur->_prev;
node* newnode = new node(x);
// prev newnode cur
prev->_next = newnode;
newnode->_prev = prev;
newnode->_next = cur;
cur->_prev = newnode;
}
iterator erase(iterator pos)
{
assert(pos._pnode);
assert(pos != end());
node* prev = pos._pnode->_prev;
node* next = pos._pnode->_next;
delete pos._pnode;
prev->_next = next;
next->_prev = prev;
return iterator(next);
}
bool empty()
{
return begin() == end();
}
size_t size()
{
size_t sz = 0;
iterator it = begin();
while (it != end())
{
++sz;
++it;
}
return sz;
}
private:
node* _head;
//size_t _size;
};
void PrintList(const list<int>& lt)
{
list<int>::const_iterator it = lt.begin();
while (it != lt.end())
{
// *it += 1; // ?
cout << *it << " ";
++it;
}
cout << endl;
}
class Date
{
public:
int _year = 0;
int _month = 1;
int _day = 1;
};
void test_list1()
{
list<int> lt;
lt.push_back(1);
lt.push_back(2);
lt.push_back(3);
lt.push_back(4);
list<int>::iterator it = lt.begin();
while (it != lt.end())
{
*it += 1;
cout << *it << " ";
++it;
}
cout << endl;
for (auto e : lt)
{
cout << e << " ";
}
cout << endl;
PrintList(lt);
}
void test_list2()
{
list<Date> lt;
lt.push_back(Date());
lt.push_back(Date());
lt.push_back(Date());
list<Date>::iterator it = lt.begin();
while (it != lt.end())
{
//cout << (*it)._year << " " << (*it)._month <<" " <<(*it)._day<
cout << it->_year << " " << it->_month << " " << it->_day << endl;
++it;
}
cout << endl;
Date d;
Date* p = &d;
(*p)._year = 100;
p->_year = 100;
}
void test_list3()
{
list<int> lt;
lt.push_back(1);
lt.push_back(2);
lt.push_back(3);
lt.push_back(4);
PrintList(lt);
list<int> copy(lt);
PrintList(copy);
list<int> lt1;
lt1.push_back(10);
lt1.push_back(20);
copy = lt1;
PrintList(copy);
PrintList(lt1);
lt.clear();
PrintList(lt);
}
}