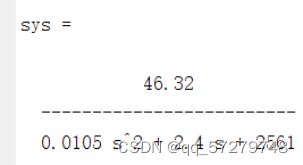基于Matlab及Simulink的机电系统仿真

实验一  基于Matlab及Simulink的机电系统仿真

 

一、实验目的

1.掌握机电系统的工程问题简化及建模的方法，会根据基本原理和规律建立数学模型。

2.根据数学模型建立仿真模型（传递函数、Simulink及状态空间模型）并进行时域和频域分析。

3.熟悉Matlab环境，并运用该工具开展仿真分析。

4.会根据仿真结果对系统进行校正。

二、实验内容

（一）不考虑刚度的情况进行以下内容实验：

（1）根据数学模型求系统的电压输入和转速的传递函数，并进行时域的阶跃响应分析并绘制时域响应曲线，并根据阶跃相应求电机的机电时间常数（电机的机电时间常数，是电动机从启动到转速达到空载转速的63.2%时所经历的时间）。

（2）编制MATLAB或Simulink程序求电机的调速特性，即不同负载力矩（学号后三位数字，x10，x100）情况下电压和转速之间的关系，填入下表，有效数据不少于20项,并在同一图中绘制出调速特性曲线。

表2 数据表表头格式

序号	电压（V）	转速（rad/s）
		空载	负载力矩M1=学号后三位数字	负载力矩M1=学号后三位数字x10	负载力矩M1=学号后三位数字x100

编制MATLAB或Simulink程序求电机的机械特性图，即不同电压情况下负载力矩和转速之间的关系。

（二）考虑刚度的情况进行以下内容实验：

（1）根据数学模型求系统的电压输入和转速的传递函数，并进行时域的阶跃响应分析并绘制时域响应曲线。

（2）建立系统的状态方程模型，并进行时域的阶跃响应分析，系统的能控性和能观性、特征值计算；以及根据状态空间模型求解电压输入和转速的传递函数，并与（1）的传递函数进行对比。

（3）根据数学模型建立Simulink模型，并进行仿真，获得仿真曲线，并根据simulink仿真模型求其传递函数。

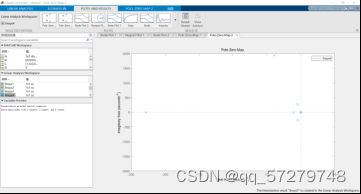
（4）绘制系统传递函数方框图，并求系统电压输入和转速为输出的开环传递函数，绘制零极点分布图、奈氏图、伯德图；并利用频域分析方法判定系统的稳定性及相对稳定性计算。

（5）求出从

正在上传…重新上传取消到的传递函数模型，并求其频率特性和根轨迹。

（6）分别取k12=0.1k12和k12=0.01k12，编制MATLAB或simulink程序，比较刚度系数不同时电机-负载模型的频率特性。

三、实验设计

1、实验的背景

技术的应用：1、MATLAB仿真的应用在各种领域，包括信号和图像处理、通讯、控制系统设计、测试和测量、财务建模和分析以及计算生物学等众多应用领域。附加的工具箱（单独提供的专用妳MATLAB函数集〉扩展了MATLAB环境，以解决这些应用领域内特定类型的问题。

2、MATLAB把工具箱延伸到了科学研究和工程应用的诸多领域，诸如数据采集、数据库接口、概率统计、样条拟合、优化算法、偏微分方程求解、神经网络、小波分析、信号处理、图像处理、系统辨识、控制系统设计、LMI控制、鲁棒控制、模型预测、模糊逻辑、金融分析、地图工具、非线性控制设计、实时快速原型及半物理仿真、嵌入式系统开发、定点仿真、DSP与通讯、电力系统仿真等。

技术的发展：

20世纪70年代中期，Cleve Moler博士和其同事在美国国家科学基金的资助下开发了调用EISPACK和LINPACK的 FORTRAN子程序库。EISPACK是特征值求解的FORTRAN程序库，LINPACK是解线性方程的程序库。在当时，这两个程序库代表矩阵运算的最高水平。

到20世纪70年代后期，身为美国New Mexico大学计算机系系主任的Cleve Moler，在给学生讲授线性代数课程时，想教学生使用EISPACK 和LINPACK程序库，但他发现学生用FORTRAN编写接口程序很费时间，于是他开始自己动手，利用业余时间为学生编写EISPACK和 LINPACK的接口程序。Cleve Moler给这个接口程序取名为 MATLAB，该名为矩阵(matrix〉和实验室( laboratory）两个英文单词的前三个字母的组合。在以后的数年里，MATLAB在多所大学里作为教学辅助软件使用，并作为面向大众的免费软件广为流传。1983年春天，Cleve Moler到Stanford大学讲学，MATLAB深深地吸引了工程师John Little。John Little敏锐地觉察到MATLAB在工程领域的广阔前景。同年，他和 Cleve Moler、Sieve Bangert一起，用C语言开发了第二代专业版。这一代的MATLAB语言同时具备了数值计在算和数据图示化的功能。1984年，Cleve Moler和 John Lithe成立了MathWorks公司，正式把MATLAB推向市场，并继续进行MATLAB的研究和开发。

在当今30多个数学类科技应用软件中，就软件数学处理的原始内核而言，可分为两大类。一类是数值计算型软件，如MATLAB、Xmath、Gauss等，这类软件长于数值计算，对处理大批数据效率高;另一类是数学分析型软件，如Mathematica、Maple等，这类软件以符号计算见长,能给出解析解和任意精度解，其缺点是处理大量数据时效率较低。MathWorks公司顺应多功能需求之潮流，在其卓越数值计算和图示能力的基础上，又率先在专业水平上开拓了其符号计算、文字处理、可视化建模和实时控制能力，开发了适合多学科、多部门要求的新一代科技应用软件MATLAB。经过多年的国际竞争，MATLAB已经占据了数值型软件市场的主导地位。

在MATLAB进入市场前，国际上的许多应用软件包都是直接以FORTRAN和C语言等编程语言开发的。这种软件的缺点是使用面窄、接口简陋、程序结构不开放以及没有标准的基库，很难适应各学科的最新发展，因而很难推广。MATLAB的出现，为各国科学家开发学科软件提供了新的基础。在MATLAB问世不久的2O世纪80年代中期,原先控制领域里的一些软件包纷纷被淘汰或在MATLAB上重建。MathWorks 公司1993年推出了MATLAB 4.0版，1995年推出4.2C版(forwin3.X) 1997年推出5.0版。1999年推出5.3版。MATLAB 5.X较MATLAB 4.X无论是界面还是内容都有长足的进展，其帮助信息采用超文本格式和PDF格式，在Netscape 3.0或IE4.0及以上版本，Acrobat Reader中可以方便地浏览。

时至今日，经过Math Works公司的不断完善，MATLAB已经发展成为适合多学科、多种工作平台的功能强劲的大型软件。在国外，MATLAB已经经受了多年考验。在欧美等高校，MATLAB已经成为线性代数、自动控制理论、数理统计、数字信号处理、时间序列分析、动态系统仿真等高级课程的基本教学工具;成为攻读学位的大学生、硕士生、博士生必须掌握的基本技能。在设计研究单位和工业部门，MATLAB被广泛用于科学研究和解决各种具体问题。

分析的意义：MATLAB和simulink仿真技术提高了科学研究水平，缩短了科学研究周期，降低了科学研究成本及风险，促进了各种不同领域学科融合、加速了科研成果转化为生产力。可以说仿真技术已成为科学研究中必不可少的使用技术。在没有出现MATLAB以前，任何研究到实验阶段都必须在硬件上实现，而MATLAB的使用使这些浪费研究资源的行动得以停止,在计算机平台上借助于MATLAB建立一个研究模型，对其输入各种参数，从而得出结果。发现其中问题后，再次改动只需改动模型，而不必改动繁琐的硬件，在研究领域得到了质的飞跃。节省了研究资源，加速了科学研究速度。

2、实验原理的设计：

由于直流电动机具有良好的启动和调速性能，常应用于对启动和调速有较高要求的场合。如大型可逆式轧钢机、矿井卷扬机、宾馆高速电梯、龙门刨床、电力机车、耐燃机车、城市电车、地铁列车、电动自行车、造纸和印刷机械、船舶机械、大型精密机床和大型起重机等生产机械中。

1.不考虑传动轴结构刚度的直流电机传动系统建模

直流电机电枢回路的电路方程是：

                         (1.1)

其中，是加到电机两端的电压；

是电机反电势；

是电枢电流；

是电枢回路总电阻；

是电枢回路总电感；

称为电枢回路电磁时间常数。

并且反电动势与电机角速度成正比：

                          (1.2)

其中，称为反电势系数；

为0

对于电机而言,其转动轴上的力矩方程为：

                       (1.3)

其中，是电机的力矩系数；

是负载力矩；

是电机电枢的转动惯量。

2、考虑传动轴结构刚度的直流电机传动系统建模

电机与负载是直接耦合的，但转动轴本质上是弹性的，存在形变，而且轴承和框架也都不完全是刚性的。对于加速度要求大、快速性和精度要求高的系统或是转动惯量大、性能要求高的系统，弹性形变对系统性能的影响不能忽略，因此在建立类似的电机-负载模型时，轴的刚度系数，即单位转角产生的力矩是一个重要参数。

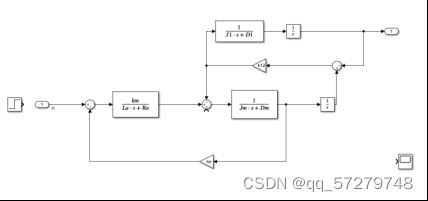
考虑到以上各种弹性体，可将被控系统视为图1所示结构，由电机、纯惯性负载以及连接二者的等效传递轴所组成的三质量系统。

图1 直流电动机传动机构负载模型

根据上面的分析并忽略轴的转动惯量，可以列出整个系统的电学方程以及动力学方程：

电动机:

                     （2.1）

                          （2.2）

                （2.3）

负载：

                       （2.4）

                     （2.5）

其中,和分别表示电动机转子和负载的转角；

、、和分别表示电动机电枢电流,电枢电压,电枢电感和电枢电阻；

、分别为电动机转子和负载的转动惯量；

表示电机的负载力矩；

和分别表示电机的电磁力矩系数和反电势系数；

表示轴的刚度系数；

和分别表示电机和框架的粘性阻尼系数。

一般地，弹性变形与机械装置的结构、尺寸、材料和受力情况有关。从系统特性分析，弹性变形使执行轴转角和负载转角之间存在一个振荡环节，从复平面上看，该振荡环节对应一对距离虚轴很近的共轭复根，阻尼系数小。这样的震荡环节具有较高的谐振峰值。如果谐振频率处于系统通频带之外，则可认为其对系统动态性能无影响；反之，若谐振频率处于系统通频带之内，则对系统影响较大。

实验参数如表1.

表1实验所需具体参数

参数	参数值	备注
电枢电阻Ra	4.80Ω
电枢电感La	21mH
力矩系数km	46.32N.m/A
反电势系数ke	55.3V/(rad/s)
电机转动惯量Jm	0.5Kg.m2	电枢部分
电机阻尼系数Dm	40Nm/(rad/s)
负载转动惯量JL	25 Kg.m2	折合到转动轴上
DL+Dm	270Nm/(rad/s)
轴刚度k12	32000Nm/度	建模时应转换为国际标准单位

四、实验步骤

工程1：（一）不考虑刚度的情况进行以下内容实验：

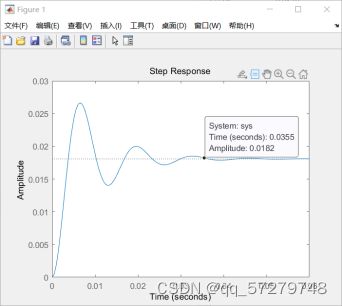
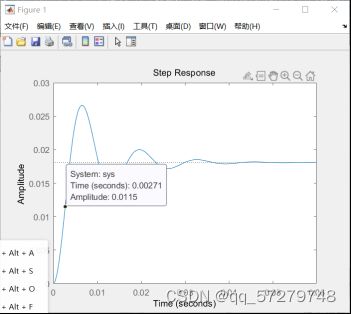
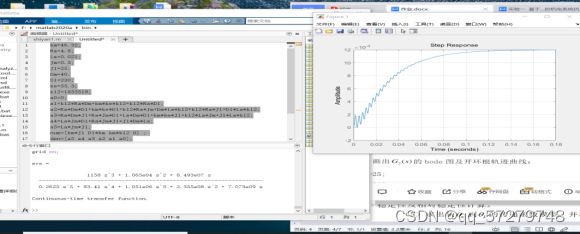
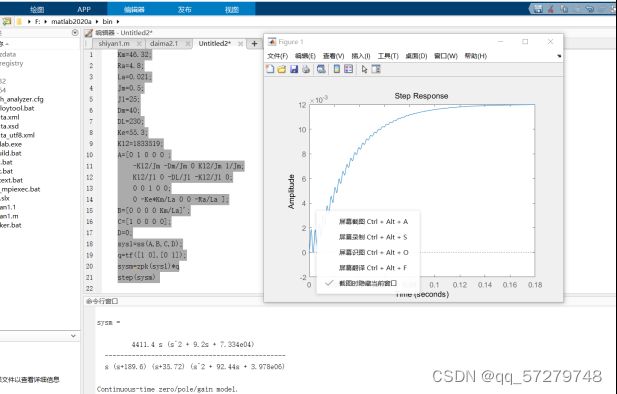
clear ;
Ra=4.8;
La=0.021;
Km=46.32;
Ke=55.3;
Jm=0.5;
T1=La/Ra;
M1=0;
num=[-M1*Ra*T1 Km-M1*Ra] ;
den=[Ra*Jm*T1 Ra*Jm Km*Ke];
sys=tf (num,den) 
y=step(sys) ;
step(sys);
得到最终的传递函数和阶跃响应如图所示：

 得到电机的稳态值大概是0.0182，电机的机电时间常数（电机的机电时间常数，是电动机从启动到转速达到空载转速的63.2%时所经历的时间），所以0.0182×0.632大概=0.0114，然后找到对应的点，看到其对应的时间大概是0.0027s。

 结论：电机有超调量并且要振荡，稳定性差，但是快速性好，能够很快的手链到稳态值。

 

（2）编制MATLAB或Simulink程序求电机的调速特性，即不同负载力矩（学号后三位数字，x10，x100）情况下电压和转速之间的关系，填入下表，有效数据不少于20项,并在同一图中绘制出调速特性曲线。

表2 数据表表头格式

序号	电压（V）		转速（rad/s）
			空载	负载力矩M1=学号后三位数字			负载力矩M1=学号后三位数字x10		负载力矩M1=学号后三位数字x100
0	0	0			-0.5845	-5.845		-58.45
1	10	0.1812			-0.4054	-5.684		-58.47
2	20	0.3624			-0.2242	-5.503		-58.29
3	30	0.5436			-0.04298	-5.322		-58.11
4	40	0.7247			-0.1382	-5.141		-57.93
5	50	0.9059			-0.3194	-4.959		-57.75
6	60	1.087			0.5002	-4.779		-57.57
7	70	1.267			0.6805	-4.598		-57.39
8	80	1.448			0.8613	-4.418		-57.21
9	90	1.629			1.042	-4.236		-57.02
10	100	1.810			1.224	-4.055		-56.84
11	110	1.991			1.404	-3.874		-56.66
12	120	2.173			1.586	-3.693		-56.48
13	130	2.354			1.768	-3.511		-56.30
14	140	2.535			1.948	-3.331		-56.12
15	150	2.716			2.129	-3.150		-55.94
16	160	2.898			2.311	-2.968		-55.76
17	170	3.079			2.492	-2.786		-55.57
18	180	3.260			2.674	-2.605		-55.39
19	190	3.444			3.316	-2.424		-55.12
20	200	3.621			3.035	-2.244		-55.03

编制MATLAB或Simulink程序求电机的调速特性，即不同负载力矩（学号后三位数字，x10，x100）情况下电压和转速之间的关系，填入下表，有效数据不少于20项,并在同一图中绘制出调速特性曲线。

表2 数据表表头格式

 

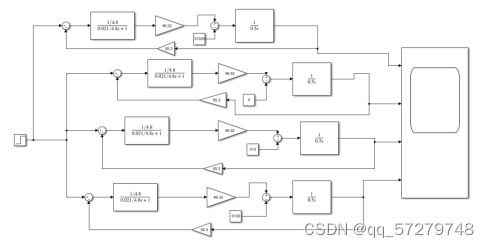
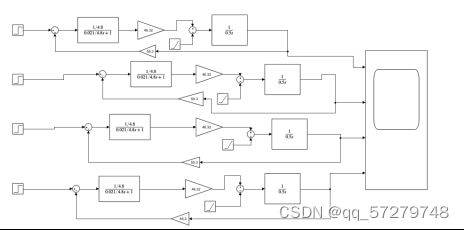
图4电机的调速特性的simulink图

同一图中绘制出调速特性曲线：把四中不同情况的负载力矩图像点击Logging,把四种情况发到工作空间并运

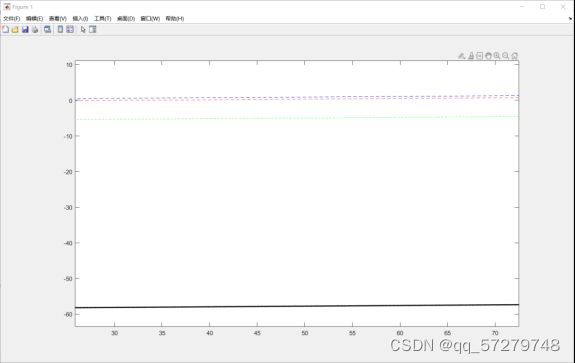
plot(out.ScopeData3(:,1),out.ScopeData3(:,2),'k',out.ScopeData5(:,1),out.ScopeData5(:,2),'b--',out.ScopeData6(:,1),out.ScopeData6(:,2),'r--',out.ScopeData7(:,1),out.ScopeData7(:,2),'g--')，

图5调速特性曲线

结论：由此图可以看出随着电压的增大，在负载力矩不变的时候，转速会跟着电压增大而增大。

 

（3）编制MATLAB或Simulink程序求电机的机械特性图，即不同电压情况下负载力矩和转速之间的关系。

 思路：因为要求不同电压下不同的输入负载，所以把输入的负载用一个一次函数表示，我取的是y=100x+c；

 

图7 机械特性图

结论：在电压不变的情况下，转速随着负载力矩的增大而减小；同时电机的机械特性硬，力矩增大，但是变化很小，我的图仿真时间为2000s，变化情况才比较看得出来。

 

工程2：（二）考虑刚度的情况进行以下内容实验：

（1）根据数学模型求系统的电压输入和转速的传递函数，并进行时域的阶跃响应分析并绘制时域响应曲线。

同样通过计算已经给定的相关数据算出传递函数：

km=46.32;
Ra=4.8;
La=0.021;
Jm=0.5;
J1=25;
Dm=40;
D1=230;
ke=55.3;
k12=1833519;
a0=0;
a1=k12*Ra*Dm+km*ke*k12+k12*Ra*D1;
a2=Ra*Dm*D1+km*ke*D1+k12*Ra*Jm+Dm*La*k12+k12*Ra*J1+D1*La*k12;
a3=Ra*Dm*J1+Ra*Jm*D1+La*Dm*D1+km*ke*J1+k12*La*Jm+J1*La*k12;
a4=La*Jm*D1+Ra*Jm*J1+J1*Dm*La;
a5=La*Jm*J1;
num=[km*J1 D1*km km*k12 0] ; 
den=[a5 a4 a3 a2 a1 a0];
sys=tf(num,den)
y=step(sys) ;
step(sys);
grid on;

 图9 阶跃响应图像

图10 传递函数

 建立系统的状态方程模型，并进行时域的阶跃响应分析，系统的能控性和能观性、特征值计算；以及根据状态空间模型求解电压输入和转速的传递函数，并然后把X1、X2、X3、X4、X5的一阶导的A、B、C、D函数化出来，依据这个写出对应的代码，得到时域的阶跃响应，如图：与（1）的传递函数进行对比。

在慕课搜索《现代控制理论》浙江大学版1.2.1章，根据视频例题将本题状态空间算出来了。先将每个复杂模块化成对应的最简单回路，然后将简单回路代替原理的方框图，并在图上标记X1、X2、X3、X4、X5和X1、X2、X3、X4、X5的一阶导，这个时候他们的关系就非常明确。

 图12 时域的阶跃响应图

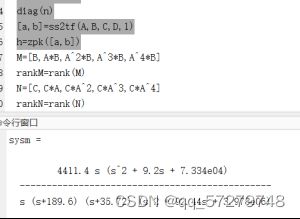
阶跃响应代码：km=46.32;
Ra=4.8;
La=0.021;
Jm=0.5;
J1=25;
Dm=40;
D1=230;
ke=55.3;
k12=1833519;
a0=0;
A=[0 1 0 0 0 ;
    -K12/Jm -Dm/Jm 0 k12/Jm 1/Jm;
    k12/J1 0 -DL/J1 -k12/J1 0;
    0 0 1 0 0;
    0 -ke*km/La 0 0 -Ra/La ];
B=[0 0 0 0 Km/La]';
C=[1 0 0 0 0];
D=0;
sys1=ss(A,B,C,D);
q=tf([1 0],[0 1]);
sysm=zpk(sys1)*q
step(sysm) ;

能控性和能观性代码：

M=[B,A*B,A^2*B,A^3*B,A^4*B]
rankM=rank(M)
N=[C,C*A,C*A^2,C*A^3,C*A^4]
rankN=rank(N)

特征值与特征向量的代码

[m,n]=eig(A)
diag(n)

 图16 状态空间模型求传递函数

状态空间模型求传递函数代码：

[a,b]=ss2tf(A,B,C,D,1)
h=zpk([a,b])

 

 图17的传递函数                图18的传递函数

结果：经过对比（1）的函数化简之后与（2）的传递函数一致。

根据数学模型建立Simulink模型，并进行仿真，获得仿真曲线，并根据simulink仿真模型求其传递函数。

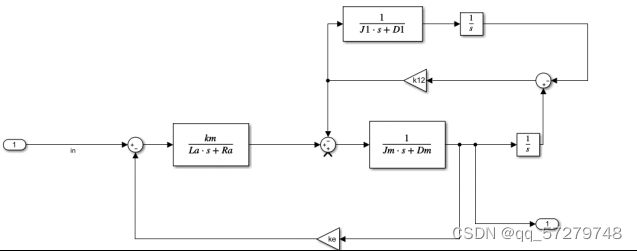
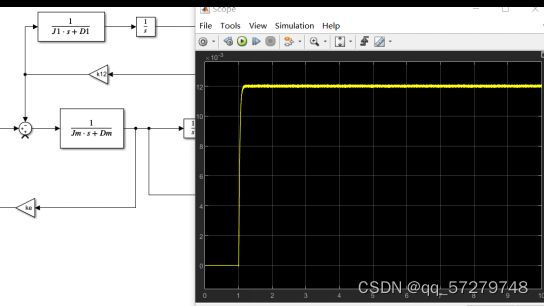
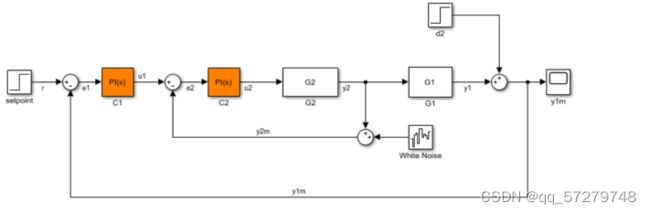
 图19 Simulink模型

---

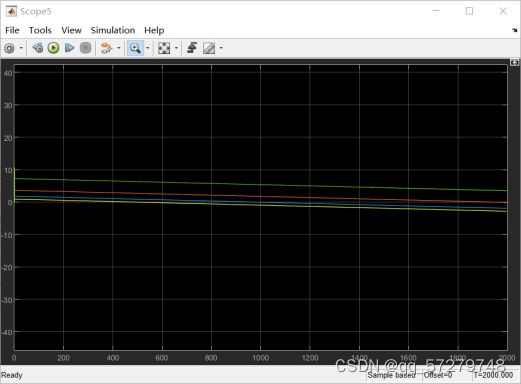
 图20仿真曲线

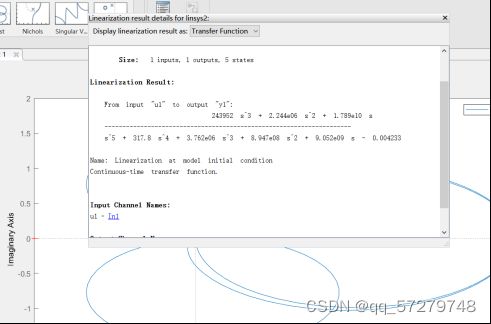
传递函数：可以从simulink方框图转传递函数，所以我在网上找到了方法（链接https://wenku.baidu.com/view/9bd6b90f4873f242336c1eb91a37f111f1850d82.html）在simulink点击→apps→→（1.在A哪里有四十I/Os选择root level inports and outports.2.点击result viewer.3.选择一个伯德图或者奈斯图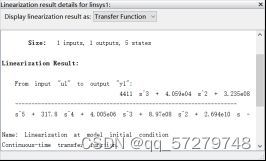）→或者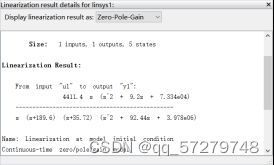最终根据题的要求就得到相应形式的传递函数。

（4）绘制系统传递函数方框图，并求系统电压输入和转速为输出的开环传递函数，绘制零极点分布图、奈氏图、伯德图；并利用频域分析方法判定系统的稳定性及相对稳定性计算。

 方法一：直接硬算它的开环传递函数，

代码：km=46.32;
Ra=4.8; 
lLa=0.021;
Jm=0.5;
J1=25;
Dm=40;
D1=230;
ke=55.3;
k12=32000*180/pi;
sys1=tf([0 km],[La,Ra]);
sys2=tf([0 1],[Jm,Dm]);
sys3=tf([k12*J1,k12*D1],J1,D1,k12]);
sys4=minreal(sys2/(1+sys2*sys3));
sys6=tf([o ke],[0 1]);
sys5=minreal(sys1*sys4*sys6);
num=[243952,2.244e06,1.789e10,0 ];
den=[1,317.8,3.761e06,8.947e08,9.052e09]
subplot(2,2,1),zplane(num, den);grid on
subplot(2,2,2),bode(sys5);grid on
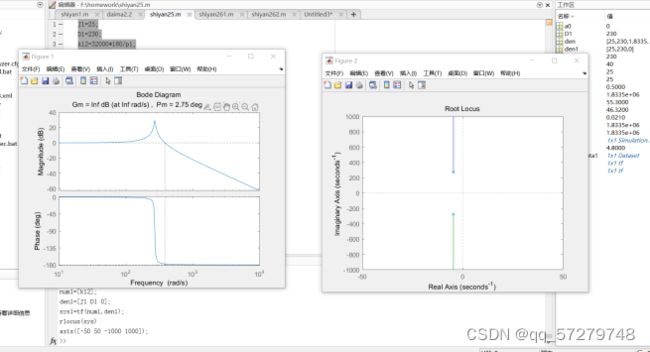
subplot(2,2,3),nyquist(sys5);grid on

 方法二：由上一题的方法我把开环传递函数方框图画出来，用同样的方式可直接得到零极点分布图、奈氏图、伯德图与开环传递函数。

 

图22零极点分布图

 

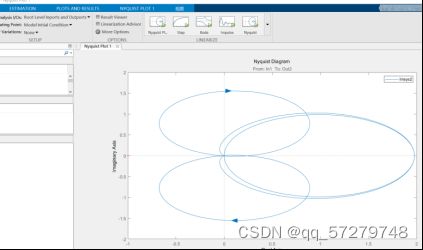
 图23奈氏图

 

 图25开环传递函数

频域判定方法：由零极点分布图可知全部的特征根都具有负实部；传递函数的全部极点都在[s]平面的左半部分所以系统稳定，

由奈氏图可知：对于开环系统奈氏系统，它的开环nyquist轨迹不包围（-1.0）点，则其闭环系统稳定。

有伯德图可知：上图单位为db是幅值裕度，下图单位为deg是相位裕度，由开环系统的对数幅频特性曲线比对数相频特性先交于横轴，则闭环系统稳定，此伯德图刚好满足，所以闭环系统稳定。

求出从到的传递函数模型，并求其频率特性和根轨迹。

先解出传递函数

传递函数代码：

Jl=25;
Dl=230;
k12=32000*180/pi;
num=[k12];
den=[Jl Dl k12];
sys=tf(num,den);
bode(sys)
margin(sys)
figure(2);
num1=[k12]; 
den1=[Jl Dl 0];
sys1=tf(num1,den1);
rlocus(sys)
axis([-50 50 -1000 1000]);

得到伯德图与根轨迹的图：

 图27伯德图与根轨迹

从伯德图看出传递函数有超调量，通过根轨迹可以看出传递函数有两个共轭复根，表明传递函数系统的阻尼系数小、振荡强、稳定性不是很好。

分别取k12=0.1k12和k12=0.01k12，编制MATLAB或simulink程序，比较刚度系数不同时电机-负载模型的频率特性

本题我还是利用simulink结构图找到传递函数，最后根据传递函数编写代码找到他们的频率特性图。先将k12=183351.9赋值给k12，然后运行simulink结构图，通过simulink转化得到一个传递函数。

 图28 Simulink方框图

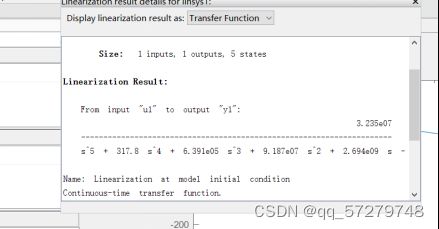
图29 k12=183351.9的传递函数

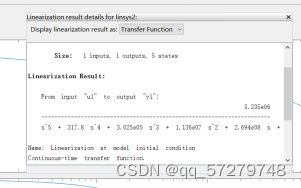
然后将k12=18335.19赋值给k12，然后运行simulink结构图，通过simulink转化得到另一个传递函数。

 图30 k12=18335.19的传递函数

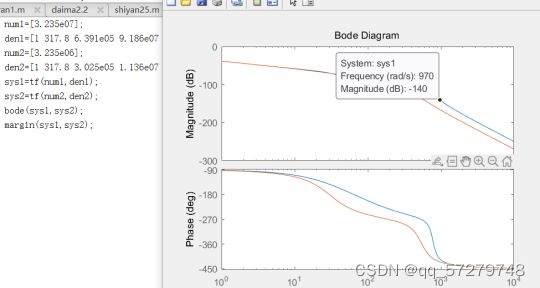
然后根据这两个传递函数写出对应的传递函数代码：

den1=[1 317.8 6.391e05 9.186e07 2.694e09 0.0003679];
num2=[3.235e06];
den2=[1 317.8 3.025e05 1.136e07 2.694e08 3.428e-06];
sys1=tf(num1,den1);
sys2=tf(num2,den2);
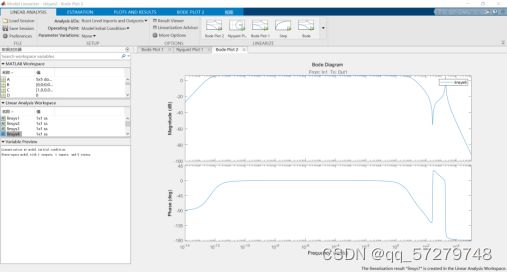
bode(sys1,sys2);
margin(sys1,sys2);

求得他们的伯德图，并利用margin函数把两个函数的图集中在一个图里面方便对比，能够看出他们的不同。

 图31 两函数的伯德图

图31 两函数的伯德图

从伯德图中可以看出蓝色线条是k12=183351.9的函数伯德图，橙色是

k12=18335.19的函数伯德图，当k12（刚度系数）变大的时候函数的幅值裕度会变大，表明刚度系数越大，整个系统的稳定性越好，反应时间更快，抗干扰能力更强。

• 思考题

状态方程分析的阶跃响应会出现多个响应曲线图，分别代表什么意思？

答：阶跃响应的响应函数就是反应整个系统的稳定性，更能反应系统的内部状态变化，多个就是反应时域分析是分析上升时间、峰值时间、最大超调量、调整时间、震荡次数。

为什么进行时域分析用的是闭环传递函数，而用频域分析通常分析的是系统的开环传递函数？开环传递函数如何表征系统的特性的？

答：时域分析用闭环函数是因为时域分析是分析上升时间、峰值时间、最大超调量、调整时间、震荡次数等，只有闭环系统才能描绘动态特性这些并判断系统的稳定性。

频域分析用开环是因为，首先闭环求解相对于开环函数更加复杂，第二对于闭环的稳定性，可以通过开环传函（如根轨迹，频域的相对裕度）进行分析，对于闭环系统的性能，则需要根据闭环的零极点分布来确定。将模型转化换到频率域研究。从而使复杂的计算过程变成直观的图示形式，并将系统动静态性能以新的指标形式清晰地展现出来。

查阅相关资料，了解Matlab中的slLinearizer、getIOTransfer，getLoopTransfer，getSensitivity和getCompSensitivity这些函数的功能，并进行示例说明。

slLinearizer：可以在不同的工作点交互线性化模型，通过修剪或模拟模型交互获得工作点，执行非线性模型的精确线性化，及非线性模型的频率响应；针对不同参数值批量生成线性化模型，用于执行线性化任务的MATLAB代码。

例：

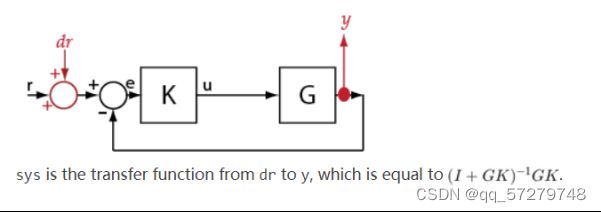
getIOTransfer：对sllinear或slTuner接口的指定I/O集的传递函数进行使用。用法如下：sys = getIOTransfer(s,in,out,temp_opening) 在temp_opening指定考虑额外的输入。例如，在反馈回路打开的情况下，使用输入来获得与设备串联的控制器的传递函数。

 

获取ex _ scd _ simple _ fdbk模型从参考信号r到工厂输出y的闭环传递函数。

打开Ex _ Scd _ Simple _ Fdbk模型。

getSensitivity：使用sllinear或slTuner接口的指定点灵敏度函数，用法如下linsys = getSensitivity(s,pt,temp_opening) ，在temp_opening指定的点考虑额外的临时洞口。例如，使用开口来计算外环打开时内环的灵敏度函数。

 

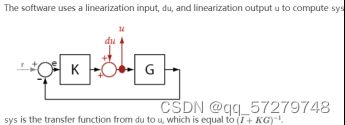
 getCompSensitivity：使用sllinear或slTuner接口在指定点实现互补灵敏度功能。用法如下：linsys = getCompSensitivity(s,pt)，返回与sl线性化器或slTuner接口s相关的模型在指定分析点的互补灵敏度函数，软件在计算linsys时会强制执行为s指定的所有永久开口。配置s.Parameters和/或s.OperatingPoints，getCompSensitivity将执行多次线性化，并返回一组互补的灵敏度函数。例：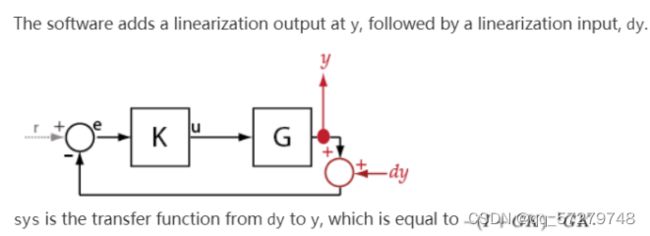

 

4简述电机机电时间常数的含义以及物理意义，对电机动态特性的影响。

含义：机电时间常数用来描述机电传动系统过渡过程的快慢。

物理意义：是电动机从启动到转速达到空载转速的63.2%时所经历的时间。加快机电传动系统的过渡过程有。有两种方法：1.减少系统的飞轮转矩GD2,2.增加动态转矩Td.