2023.03.12 学习周报

---

摘要

This week, I read an article related to the sequential recommendation system, The Top-N sequential suggestion model treats each user as a sequence of past interactions and aims to predict that the user will participate in Top-N ranked projects in the future, Interaction order means that sequential patterns play an important role in interactions. In this paper, an interactive inference model is applied to images in time and potential space, and it is applied to the transformation filter as the local feature of the image; The method provides a unified and flexible network structure for capturing general preferences and order trends; Experiments on public data sets show that the model outperforms the most advanced experience-based methods. In addition, I learn principal component analysis and optimization methods; In the process of learning principal component analysis, it is mainly divide into two aspects. On the one hand, it is the key point of PCA dimension reduction, which explains why the matrix formed by eigenvectors corresponding to eigenvalues of covariance can achieve the effect of dimension reduction. On the other hand, it introduces a solution method of PCA principal eigenvectors, namely singular value decomposition; In the process of learning optimization methods, I mainly introduce two methods, namely gradient descent method and Newton method, and explain their principles through mathematics. Finally, I realize these two methods through python.

本周，我阅读了一篇与顺序推荐系统相关的文章，Top-N顺序建议模型将每个用户视为过去交互的序列，并旨在预测用户在未来将参与Top-N排名的项目，交互顺序意味着顺序模式在交互中起着重要作用。对此，文章提出了一种将交互推理模型应用于时间和潜在空间中的图像，并将其作为图像的局部特征应用于转换过滤器；该方法提供了一种统一和灵活的网络结构，用于捕获一般偏好和顺序趋势；在公共数据集上的实验表明，该模型优于最先进的基于经验的方法。此外，我学习了主成分分析和最优化方法；在学习主成分分析的过程中，主要分为两方面，一方面是PCA降维的关键点，解释了为什么协方差的特征值对应的特征向量构成的矩阵能够实现降维的效果，另一方面是介绍PCA主特征向量的一种解法，即奇异值分解；在学习最优化方法的过程中，我主要介绍了两种方法，即梯度下降法和牛顿法，并通过数学去解释其中的原理，最后通过python去实现了这两种方法。

---

文献阅读

1.题目

文献链接：Personalized Top-N Sequential Recommendation via Convolutional Sequence Embedding

2.摘要

Top-N sequential recommendation models each user as a sequence of items interacted in the past and aims to predict top-N ranked items that a user will likely interact in a “near future”. The order of interaction implies that sequential patterns play an important role where more recent items in a sequence have a larger impact on the next item. In this paper, we propose a Convolutional Sequence Embedding Recommendation Model (Caser) as a solution to address this requirement. The idea is to embed a sequence of recent items into an “image” in the time and latent spaces and learn sequential patterns as local features of the image using convolutional filters. This approach provides a unified and flexible network structure for capturing both general preferences and sequential patterns. The experiments on public data sets demonstrated that Caser consistently outperforms state-of-the-art sequential recommendation methods on a variety of common evaluation metrics.

3.介绍

在大多数系统中，Top-N 顺序推荐都只是基于用户的general preferences，而没有考虑到最近的情况。另一类用户行为是sequential patterns，即用户的下一个交互物品（动作）更可能和用户最近的活动（最近交互的物品）有关。

3.1 Top-N Sequential Recommendation

给定用户 U 与物品的交互序列 Su = (Su1,…,Su|Su|)，其中|Su|表示的是用户与物品交互的相对顺序，即Su1表示用户u交互的第一个物品。基于这个交互序列Su，目标是通过综合考虑用户的general preferences和sequential patterns，为每个用户推荐一个物品列表，以最大程度上满足用户u的未来需求。

3.2 Limitations of Previous Work

早期的 top-N sequential Recommendation 的工作是基于马尔可夫链的，而 L-阶马尔可夫链式是基于前 L 个动作进行推荐的。本质上，一阶马尔科夫链就是通过极大化似然估计来学习一个 item-to-item 的转移矩阵。基于马尔可夫链的工作有 FPMC、Fossi l等，但这些方法存在以下几种限制：
1）没有建模 union-level sequential patterns
基于马尔科夫链的模型只考虑了 point-level sequential patterns，也就是说，它只是考虑了之前的每个行为单独对目标行为产生的影响。Fossil 虽然考虑了高阶马尔科夫链，但是它只是将每个物品的潜表示进行了权重和操作，这并不足以忽视建模 union-level的影响。

2）没有允许 skip behavior
skip behaviors是指过去的行为可能会跳过几步，但仍然对后续动作是有强影响的。这是基于马尔可夫链的方法不能做到的。
文章做了一个小实验去证实上面提到的两种观点：

3.3 主要贡献

1）通过使用水平和垂直两个过滤器，Caser 可以捕捉到point-level，union-level和skip behaviors;
2）Caser 可以同时建模用户的 general preferences 和 sequential patterns，并且在单个统一框架中概括了几种现有的最先进的方法。

4.Proposed Methodology

该模型分别采用卷积神经网络和隐因子模型 (LFM)来学习序列特征和用户特征：
1）Caser 网络设计的目标是在 union-level 和 point-level 中捕获用户的一般偏好和顺序模式，并捕获跳过行为，所有这些都在未观察到的空间中。
2）Caser 由三个部分组成，embedding layer，convolutional layer, fully-connected layer。对于每个用户u，我们从用户序列 Su 中提取每 L 个连续项作为输入，并将它们的下一个 T 项作为目标。这是通过在用户序列上滑动一个大小为 L +T 的窗口来实现的，每个窗口都为 u 生成一个训练实例，它由一个三元组(u、前L项、后T项)表示。

4.1 Embedding Look-up

Caser 通过将前 L 个物品的 embedding（其中第 i 个物品的 embedding 表示为 Qi ）送入神经网络中去捕捉顺序特征。Embedding look-up 操作就是将 L 个物品的embedding 堆叠在一起，生成一个矩阵E(u, t)，u指的是用户u，t指的是time step。

除了 item embedding，对于每个用户 u，我们还有一个embedding Pu ∈ R^d，而这里的Pu是通过参数学习的。

4.2 Convolutional Layers

通过将前 L 个物品构成的 L×d 矩阵 E 视为这 L 个物品在潜空间中的一个“图像“，就可以将sequential patterns 看成是这个图像的局部特征，这样就得到了 sequential　patterns。
1）Horizontal Convolutional Layer
这里需要n个水平过滤器，每个过滤器表示为F^k∈R（h×d）h∈{1,…,L}，其中F ^k：指的是第k个过滤器；h是过滤器的高度；d是物品的embedding维度。

如果选择前L个物品L=4，则h∈{1，2，3，4}。如果每个h有两个过滤器的话，那我们就有了8个过滤器。这里有一个问题：如果一个高度对应两个过滤器，怎么保证两个过滤器学到不一样的特征？

现在考虑第k个滤波器，F^k从矩阵E的顶部到底部滑动，从水平维度上与物品进行交互，每一次卷积操作如下：

则第k个过滤器的结果为一个向量c^ k，然后通过max pooling得到第k个滤波器抽取的最重要的特征max(c^k)，最终我们得到n个过滤器捕捉到的所有特征表示为o。至此，我们就得到了union-level patterns。
2）Vertical Convolutional Layer
假设有_n个垂直过滤器_F^ k ∈R L×1，每一个垂直过滤器_F^k 通过在矩阵E上从左到右滑动d次，产生一个垂直的卷积结果_c ^ k。

对于内积计算来说，很容易证明这个结果等价于矩阵E的L行上的加权求和，其中_F^k为权重，这样我们就可以聚合前L个物品的embedding。通过_n个垂直过滤器，对每个用户我们有_n个加权和。因为我们希望保持每个潜在维度的聚合，所以不需要对垂直卷积结果进行最大池化操作。

这里有一个问题：这样学习到的_n个加权和表示什么意思？_n个不同聚合的优势在哪里？

4.3 Fully Connected Layer

将两个卷积结果级联起来送入全连接层，通过全连接层，我们可以得到more high-level and abstract的特征z：

最后，为了捕捉用户的general preferences，我们将z和user embedding级联起来，并进行如下计算得到最终输出值：

5.实验

1）数据集

文章认为只有当数据集包含顺序模式时，顺序推荐才有意义。因此，为了识别这类数据集，文章将序列关联规则挖掘应用于多个公共数据集，并计算它们的序列强度：

将每个用户序列中70%的操作作为训练集，并使用接下来10%的操作作为验证集来针对所有模型搜索最优超参数设置，每个用户序列中其余20%的操作用作评估模型性能的测试集。
2）测量准则
文章采用Prec@N、Recall@N、MAP作为指标：

其中：R是测试集中的目标物品，R1:N为模型预测的Top-k个物品，MAP则为所有用户AP的均值。

3）实验结果

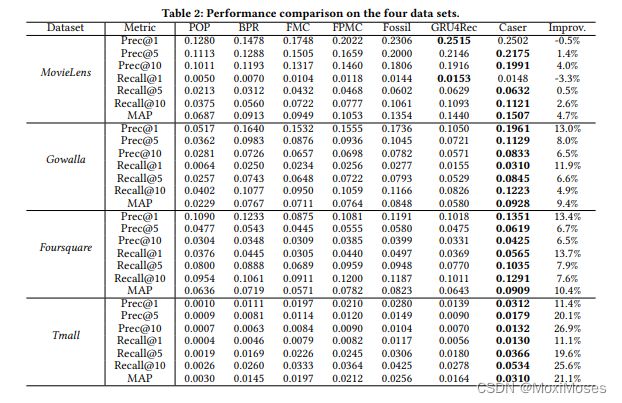
6.结论

文章提出的 Caser 是一种针对 top-N 顺序推荐的新颖方案，它将最近的行为建模为时间和潜在维度之间的“图像”，并使用卷积滤波器学习顺序模式。该方法提供了一种统一和灵活的网络结构，用于捕获顺序推荐的许多重要特征：1）点级和联合级顺序模式；2）skip behaviors；3）长期用户偏好。而在公共现实生活数据集的实验研究中表明，Caser 在 top-N 顺序推荐领域优于最先进的方法。

深度学习

1.主成分分析

1.1 PCA步骤的关键点

关键点：为何协方差的特征值对应的特征向量构成的矩阵能够实现降维的效果？

给定一个单位向量μ和空间内一点Xi，Xi在μ上的投影与原点的距离为μTXi。如果Xi为数据集合X中的一点，因此为了最大化投影点的方差，我们需要选择一个单位向量μ将如下式子最大化：

问题是求方差最大化，如果μ越大的话，总体方差也就越大。现我们只想求μ的方向，而不想依赖于μ的长度，于是我们让μ为一个标准化的向量，即为单位向量。接下来， 我们可以通过拉格朗日乘子法构造下面方程：

上图中λ是一个常数，可以将μλμT变成λμμT，又因为μμT = 1，得到μλμT=λ。

通过上面的推导，我们可以得出结论，PCA降维就是去求协方差矩阵的特征值和特征向量。

1.2 sklearn实现PCA降维

import numpy as np
from sklearn.decomposition import PCA

X = np.array([[2.1, 2.9],
              [0.5, 0.4],
              [2.5, 2.7],
              [1.2, 2.9],
              [3.9, 3.2],
              [2.1, 2],
              [2.3, 1.7],
              [1, 1.6],
              [1, 1.1],
              [1.5, 0.6]])

pca = PCA(n_components=1)  # 把二维的原数据降成一维
newX = pca.fit_transform(X)  # 把原数据X传入方法，返回降维后的数据
invX = pca.inverse_transform(newX)  # 将降维后的数据转换成原始数据

print(X)
print(newX)
print(invX)
print(pca.explained_variance_ratio_)  # 返回保留的n个成分各自的方差贡献比

原数据：

降维后的数据：

将降维后的数据转换成原数据，存在偏差：

主成分方差贡献比，84%的占比表示这1个维度就可以很好的代表原来的高维度数据：

1.3 主成分个数的选择

1）百分比截点（Percentage cutoff）
使用足够多的主成分，来反映一定百分比的总方差。
2）平均比截点（Average cutoff）
使用特征值大于平均特征值的主成分；平均截点准则被广泛使用，是很多软件包的默认准则；当数据能够在相对较小的维度下被很好地归纳时，特征值可以明显地分为“大特征值”和“小特征值”。
3）碎石图 (Scree graph)
画出λj关于j的图像，从图上寻找能区分“大特征值”和“小特征值”的分界点。

2.奇异值分解

2.1 SVD 定义

SVD 可以看成是对 PCA 主特征向量的一种解法，为了求数据的主特征方向，我们通过求协方差矩阵的特征向量来表示样本数据的主特征向量，但其实我们可以通过对X进行奇异值分解得到主特征方向。

SVD 也是对矩阵进行分解，但是和特征分解不同，SVD并不要求要分解的矩阵为方阵。假设我们的矩阵A是一个m行×n列的矩阵（只有行数m > 列数n的矩阵时，才能进行 SVD 分解），那么我们定义矩阵A的SVD为：A = UΣ VT。

其中：U 是一个 mm 的矩阵，Σ 是一个 mn 的矩阵，除了主对角线上的元素以外全为0，主对角线上的每个元素都称为奇异值， V 是一个 n*n 的矩阵。

2.2 求出SVD分解后的U,Σ,V

1）V矩阵：将A的转置和A做矩阵乘法，得到n×n的一个方阵AT A，得到的特征值和特征向量满足下式：(AT A)vi = λivi。这样可以得到矩阵AT A 的n个特征值λi和对应的n个特征向量vi。将AT A的所有特征向量组成一个n×n的矩阵V，这就是 SVD 公式里面的V矩阵了。一般我们将V中的每个特征向量叫做A的右奇异向量。

2）U矩阵：将A和A的转置做矩阵乘法，得到m×m的一个方阵A AT，得到的特征值和特征向量满足下式：(A AT)ui = λiui。这样可以得到矩阵A AT的m个特征值λi和对应的m个特征向量ui。将A AT的所有特征向量组成一个m×m的矩阵U，这就是 SVD 公式里面的U矩阵了。一般我们将U中的每个特征向量叫做A的左奇异向量。

3）由于Σ除了对角线上是奇异值其他位置都是0，那我们只需要求出每个奇异值σ即可：

2.3 总结

1）特征值矩阵等于奇异值矩阵的平方，即可以通过求出AT A的特征值取平方根来求奇异值；
2）左奇异矩阵可以用于行数的压缩；
3）右奇异矩阵可以用于列数的压缩（特征维度的压缩），即PCA降维。

2.4 SVD算法的python实现

import numpy as np

X = np.array([[2.1, 2.9],
              [0.5, 0.4],
              [2.5, 2.7],
              [1.2, 2.9],
              [3.9, 3.2],
              [2.1, 2],
              [2.3, 1.7],
              [1, 1.6],
              [1, 1.1],
              [1.5, 0.6]])

meanVals = np.mean(X, axis=0)  # 求X各列均值
meanRemoved = X - meanVals  # 减去原始数据中的均值，避免协方差计算中出现乘以0的情况
U, sigma, VT = np.linalg.svd(meanRemoved)  # svd分解

print(U)
print(sigma)
print(VT)

U,Σ,V的输出：

3.最优化方法

大部分的机器学习算法的本质都是建立优化模型，通过最优化方法对目标函数或损失函数进行优化，从而训练出最好的模型。

3.1 梯度下降法

梯度下降法（Gradient Descent）是最常用的最优化方法：梯度下降法实现简单，当目标函数是凸函数时，梯度下降法的解是全局解；在一般情况下，其解不保证是全局最优解，梯度下降法的速度也未必是最快的；梯度下降法的优化思想是用当前位置负梯度方向作为搜索方向，因为该方向为当前位置的最快下降方向，越接近目标值，步长越小，前进越慢。

3.1.1 梯度下降的理解

当我们处在一座大山上的某处时，但我们不知道怎么下山，于是每走到一个位置，就去求解当前位置的梯度，沿着梯度的负方向，也就是当前最陡峭的方向向下走一步，然后重复上面的步骤，一直走到我们觉得到了山脚为止。但这样走下去，我可能走不到山脚，而是到了某一个局部的山峰低处，即局部最小值。

从上面的解释可以看出，梯度下降不一定能够找到全局最优解，很有可能是一个局部最优解。当然，如果损失函数是凸函数，梯度下降法得到的解就一定是全局最优解。

3.1.2 梯度下降法的优化

1）步长
步长取值取决于数据样本，从大到小取一些值，分别运行算法，看看迭代效果。如果损失函数在变小，说明取值有效，否则要增大步长；步长太大，会导致迭代过快，甚至有可能会错过最优解；步长太小，迭代速度太慢，很长时间算法都不能结束；所以算法的步长需要多次运行后才能得到一个较优的值。

2）参数初始值
初始值不同，获得的最小值也有可能不同，因此梯度下降求得的只是局部最小值。由于有局部最优解的风险，需要多次使用不同初始值运行算法，关键是选择损失函数最小化的初值。

3）归一化
由于样本不同特征的取值范围不一样，可能导致迭代很慢，为了减少特征取值的影响，可以对特征数据归一化。

3.1.3 梯度下降法的缺点

1）靠近极小值时收敛速度减慢；
2）直线搜索时可能会产生一些问题；
3）找到的是局部最小值，可能会呈“之”形状下降。

3.1.4 梯度下降法python实现

def train(x, y, w, b, alpha, epoch):

    dw = 0  # 权重梯度
    db = 0  # 偏差梯度
    m = x.shape[0]  # 样本数

    for i in range(epoch):
        dw = 0
        db = 0
        for j in range(m):
            w = w - alpha * (dw / m)  # 更新权重
            b = b - alpha * (db / m)  # 更新偏差
    return w, b

3.2 牛顿法

牛顿法是一种在实数域和复数域上近似求解方程的方法，使用函数f(x)的泰勒级数的前面几项来寻找方程f(x)=0的根。

牛顿法的特点：收敛速度很快。

3.2.1 牛顿法的求解方程

其实并不是所有的方程都有求根公式，又或是求根公式很复杂，导致求解困难。因此，可以用牛顿法迭代求解：

3.2.2 牛顿法的迭代公式

前面提到求解方程的过程其实是一个无约束最优化问题，而我们要找的是目标函数的极小点x*：

3.2.3 牛顿法与梯度下降法的差异

1）梯度下降法和牛顿法相比，两者都是迭代求解，但梯度下降法是梯度求解，而牛顿法是用二阶的海森矩阵的逆矩阵求解。相对而言，使用牛顿法迭代次数少，收敛更快，但是每次迭代的时间比梯度下降法长；
2）牛顿法对初始值有一定要求，在非凸优化问题中，牛顿法很容易陷入鞍点，而梯度下降法则很容易逃离鞍点；
3）梯度下降法在靠近最优点时会震荡，因此在梯度下降法中需要调整步长。

3.2.4 牛顿法python实现

import numpy as np
from torch.autograd.functional import hessian, jacobian


def newton(f, x, epoch):

    for i in range(1, epoch):
        Hessian_T = np.linalg.inv(hessian(f, x))
        H_G = np.matmul(Hessian_T, jacobian(f, x))
        x = x - H_G
        print("第{}次迭代后的结果为:".format(i + 1), x)
    return x

---

总结

本周，我学习了降维和最优化方法的相关知识；在对降维知识的学习中，主要是针对上周遗留的 PCA 降维内容进行学习，理解到了为什么协方差的特征值对应的特征向量构成的矩阵能够实现降维的效果；在对最优化方法知识的学习中，我主要学习了牛顿法和梯度下降法，理解到了其中的数学原理；下周将继续学习数据降维中非线性方法以及机器学习的相关知识。