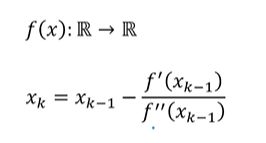一维牛顿法与多维牛顿法
Julia中文文档:https://docs.juliacn.com/latest/stdlib/LinearAlgebra/#LinearAlgebra.eigmin
牛顿法
鼎鼎有名的泰勒展开式
一元目标函数
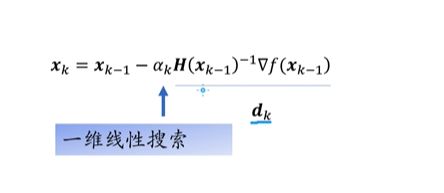
多元牛顿法
多元目标函数
牛顿法优点
收敛速度快
牛顿法缺点
- 所以牛顿法的使用并不是特别多
修正牛顿法
第一种修正方法(修正不是每一步下降)
增加了一个步长,步长用划界法或其他方法来确定,保证每步都下降(修正目的)
第二种修正方法(修正hession矩阵不是正定的)
高斯牛顿法与非线性回归
为什么非线性回归要是用牛顿法?
为非线性回归的目标函数是使残差最小,本质上还是一个求最小值的问题
原理
优化目标函数
梯度
黑塞矩阵
O矩阵的元素一般为0,可以省略
牛顿法迭代公式(包含修正)
可见高斯牛顿法只需要用到一阶偏导即可
高斯牛顿法的代码实现(Julia)
调用第三方包
using LinearAlgebra
构建方法函数
function GaosiNewton(
f, # 要拟合成的函数
g, # 梯度,是针对偏回归系数
data, # 数据,每一行代表的是一个点,前面是自变量,最后一列是响应变量
start; # 牛顿法的起始点
α0 = 1, # 步长
acc = 0.001,
maxI = 128,
debug = false,
plot = false # 是否输出迭代点
)
end
构造创建r向量以及J雅克比矩阵的函数
(放在主函数内)
function getR(para)
return mapslices(row ->f(row[1:end-1]...,para...)-row[end], data, dims = [2])
end
# 定义计算J函数
function getJ()
return mapslices(row->g(row[1:end-1]...,x0...), data, dims = [2])
end
数据的初始化
x0 = start
I = Diagonal(ones(length(start)))
r0 = getR(x0)
s0 = sum(r0 .^ 2)
输入的判断
# 取得维度
n,m = size(data)
if m < length(start)
return false
end
创造for循环
for i in 1:maxI
J0 = getJ()
g0 = J0' * r0
h0 = J0' * J0
# 求出的em是最小的特征值
# 修正黑塞矩阵
em = eigmin(h0)
if em < 0
h0 = h0-1.1*em * I
end
# Newton
if det(h0) ==0
println("i:",i,"黑塞矩阵不可逆")
return nothing
end
d = -inv(h0) * g0
# 计算步长
#α0 = searcha(f,g,x0,g(,))
# upload data
δ = α0 .* d
x = x0 .+ δ
r = getR(x)
# 目标函数值
s = sum(r .^ 2)
if plot
println(x')
end
if debug
println("i:",i,",x:",x)
println("s:",s)
println("r0",r0)
println("J0",J0)
end
# 剪测是否达到要求的精度
if abs(s - s0)/max(1,s0) < acc
println("高斯牛顿法完成")
return x,s
end
x0 = x
r0 = r
s0 = s
end
println("达到最大迭代次数,结束高斯牛顿法")
return x0,s0
end
创建测试样例
#Test
x,s = GaosiNewton(
(x,a,b) -> a + b*x^2,
(x,a,b) -> [1,x^2],
#(x,a,b) -> a + exp(b*x^2) ,
#(x,a,b) -> [1,exp(b+x^2)*x^2],
[0 1;1 0;3 2;5 4;6 4;7 5],
[100,100],
debug = false,
plot = true
)
#println(x)
#println(s)
![1584677124029)(http://127.0.0.1:8090/upload/2020/3/image-c94c972f910743c7ab78da65b11409b6.png)]](http://img.e-com-net.com/image/info8/7b0c21d4e95d4ba5b98a69463fa48bbf.jpg)