Leetcode 动态规划解决字串与子序列问题
Leetcode 动态规划学习总结
- 利用动态规划解决字串子序列问题
-
- 动态规划?
- 子串和子序列的区别?
- 最长递增子串与最长递增子序列
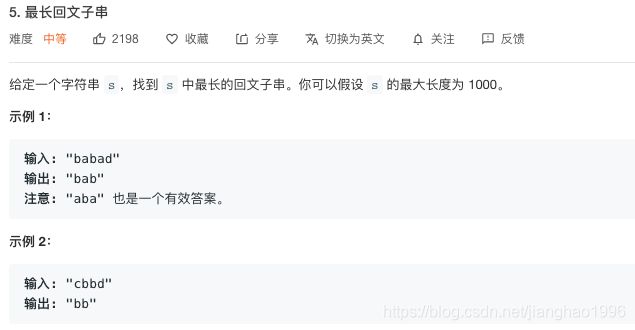
- 最长回文子串和最长回文子序列
- 最长公共子序列(LCS)与最长公共子串
- 关于子序列问题的总结
利用动态规划解决字串子序列问题
动态规划?
通过总结规律找出最优解决方案(数学归纳法)!!!
动态规划一般可分为线性动规,区域动规,树形动规,背包动规四类
子串和子序列的区别?
1.子串是字符串连续不断的一块字符串:例如"abcdefg" 则"bcd" 为其子串;
2.子序列中的字符都是字符串的子集,但是一定是顺序上是单调的:例如"abcdefg" 则"acfg"其子序列;
最长递增子串与最长递增子序列
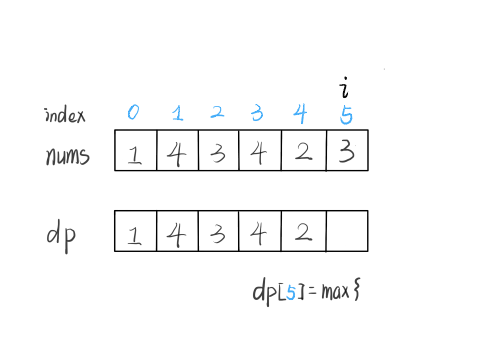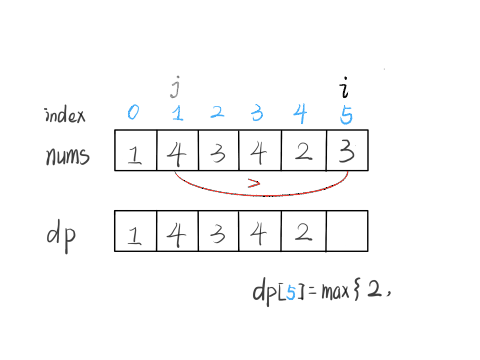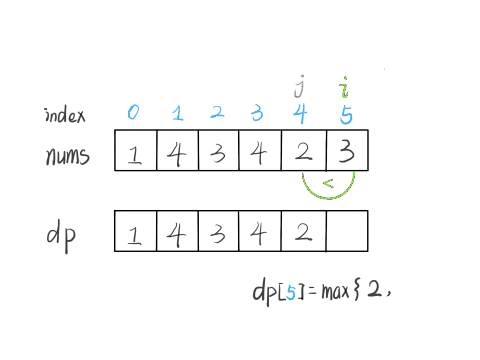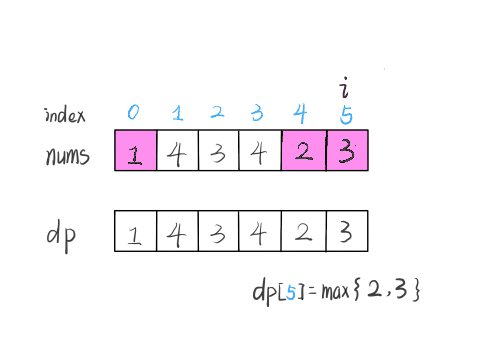
最长递增子序列(Longest Increasing Subsequence,简写 LIS)是比较经典的一个问题,比较容易想到的是动态规划解法,时间复杂度 O(N^2),我们借这个问题来由浅入深讲解如何写动态规划。比较难想到的是利用二分查找,时间复杂度是 O(NlogN),

动态规划:DP[i] = fmax(RES, DP[i - 1] + 1)
int longestSubString(std::vector<int> s)
{
std::vector<int> dp(s.size(), 0);
dp[0] = 1;
for (int i = 1; i < s.size(); ++i)
{
for(int j = 0; j < i; j++)
{
if(s[i] > s[j])
dp[i] = fmax(dp[i], dp[j] + 1);
}
}
return *max_element(dp.begin(), dp.end());
}
最长递增子串
解题思路:dp[i]:表示第i个元素,它的递增元素的个数。比如[1,3,5 ]元素3 从1递增到3 递增元素个数是2,dp[1]=2, dp=[1]*n
int findLengthOfLCIS(vector<int>& nums) {
int length = nums.size();
if(!length)
return 0;
vector<int> dp(length, 1);
int res = 1;
for(int i = 1; i < length; i++)
{
if(nums[i - 1] < nums[i])
dp[i] = dp[i - 1] + 1;
res = fmax(dp[i], res);
}
return res;
}
(2)滑动窗口
算法:
每个(连续)增加的子序列是不相交的,并且每当 nums[i-1]>=nums[i] 时,每个此类子序列的边界都会出现。当它这样做时,它标志着在 nums[i] 处开始一个新的递增子序列,我们将这样的 i 存储在变量 anchor 中。
例如,如果 nums=[7,8,9,1,2,3],那么 anchor 从 0 开始(nums[anchor]=7),并再次设置为 anchor=3(nums[anchor]=1)。无论 anchor 的值如何,我们都会记录 i-anchor+1 的候选答案、子数组 nums[anchor]、nums[anchor+1]、…、nums[i] 的长度,并且我们的答案会得到适当的更新。
int findLengthOfLCIS(vector<int>& nums) {
int pos = 0, res = 0;
int length = nums.size();
for(int i = 0; i < length; i++)
{
if(i > 0 && nums[i - 1] >= nums[i])
pos = i;
res = max(res, i - pos + 1);
}
return res;
最长回文子串和最长回文子序列
最长回文子串:主要用到的算法(1)动态规划 (2)中心扩散
class Solution {
public:
string longestPalindrome(string s) {
int n = s.size();
vector<vector<int>> dp(n, vector<int>(n));
string ans;
for (int l = 0; l < n; ++l) {
for (int i = 0; i + l < n; ++i) {
int j = i + l;
if (l == 0) {
dp[i][j] = 1;
}
else if (l == 1) {
dp[i][j] = (s[i] == s[j]);
}
else {
dp[i][j] = (s[i] == s[j] && dp[i + 1][j - 1]);
}
if (dp[i][j] && l + 1 > ans.size()) {
ans = s.substr(i, l + 1);
}
}
}
return ans;
}
};
(2)中心扩散:

可以发现,所有的状态在转移的时候的可能性都是唯一的。也就是说,我们可以从每一种边界情况开始「扩展」,也可以得出所P(i+1,j−1) 扩展到 P(i,j)P(i,j);如果两边的字母不同,我们就可以停止扩展,因为在这之后的子串都不能是回文串了。
聪明的读者此时应该可以发现,「边界情况」对应的子串实际上就是我们「扩展」出的回文串的「回文中心」。方法二的本质即为:我们枚举所有的「回文中心」并尝试「扩展」,直到无法扩展为止,此时的回文串长度即为此「回文中心」下的最长回文串长度。我们对所有的长度求出最大值,即可得到最终的答案。
string longestPalindrome(string s) {
string res;
for(int i = 0; i < s.size(); i++)
{
string r1 = Palindrome(s, i, i);
string r2 = Palindrome(s, i, i + 1);
res = res.size() < r1.size() ? r1 : res;
res = res.size() < r2.size() ? r2 : res;
}
return res;
}
string Palindrome(string& s, int left, int right)
{
while(left >= 0 && right < s.size() && s[left] == s[right])
left--, right++;
return s.substr(left + 1, right - left - 1);
}
最长回文子序列:
 状态
状态
dp[i][j] 表示 s 的第 i 个字符到第 j 个字符组成的子串中,最长的回文序列长度是多少。
转移方程
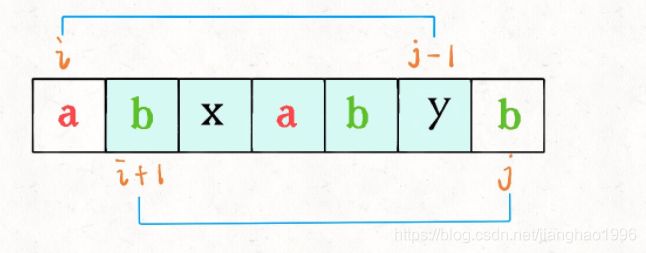
如果 s 的第 i 个字符和第 j 个字符相同的话
dp[i][j] = dp[i + 1][j - 1] + 2
如果 s 的第 i 个字符和第 j 个字符不同的话
dp[i][j] = max(dp[i + 1][j], dp[i][j - 1])
然后注意遍历顺序,i 从最后一个字符开始往前遍历,j 从 i + 1 开始往后遍历,这样可以保证每个子问题都已经算好了。
初始化
dp[i][i] = 1 单个字符的最长回文序列是 1
结果
dp[0][n - 1]
class Solution {
public:
int longestPalindromeSubseq(string s) {
int length = s.length();
vector<vector<int>> dp(length, vector<int>(length, 0));
for(int i = 0; i < length; i++)
dp[i][i] = 1;
for(int i = length - 1; i >= 0; i--)
{
// dp[i][i] = 1;
for(int j = i + 1; j < length; j++)
{
if(s[i] == s[j])
dp[i][j] = dp[i + 1][j - 1] + 2;
else
dp[i][j] = fmax(dp[i + 1][j], dp[i][j - 1]);
}
}
return dp[0][length - 1];
}
};
最长公共子序列(LCS)与最长公共子串
最长公共子序列:是一道非常经典的面试题目,因为它的解法是典型的二维动态规划,大部分比较困难的字符串问题都和这个问题一个套路,比如说编辑距离。而且,这个算法稍加改造就可以用于解决其他问题,所以说 LCS 算法是值得掌握的。
输入: str1 = "abcde", str2 = "ace"
输出: 3
解释: 最长公共子序列是 "ace",它的长度是 3
动态规划:LCS 算法使用的二维DP数组,第一步,一定要明确 dp 数组的含义。对于两个字符串的动态规划问题,套路是通用的。
if (str1[i] == str2[j])
# 这边找到一个 lcs 的元素,继续往前找
return dp(i - 1, j - 1) + 1;
else
# 谁能让 lcs 最长,就听谁的
return max(dp(i-1, j), dp(i, j-1));
完整代码如下
class Solution {
public:
int longestCommonSubsequence(string text1, string text2) {
int length1 = text1.length(), length2 = text2.length();
vector<vector<int>> dp(length1 + 1, vector<int>(length2 + 1, 0));
for(int i = 1; i < length1 + 1; i++)
{
for(int j = 1; j < length2 + 1; j++)
{
if(text1[i - 1] == text2[j - 1])
dp[i][j] = dp[i - 1][j - 1] + 1;
else
dp[i][j] = fmax(dp[i - 1][j], dp[i][j - 1]);
}
}
return dp[length1][length2];
}
};
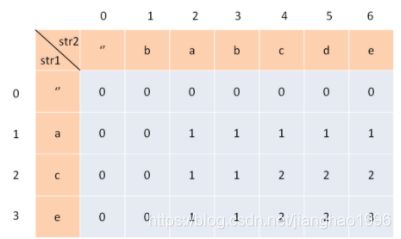
最长公共子串:给定两个序列 X 和 Y,如果 Z 即是 X 的子串,又是 Y 的子串,我们就称它是 X 和 Y 的公共子串,注意子串是连续的。
例如 X = { a, b, c, d, e},Y = {c, b, c, d, a },那么它们最长的公共子串即 { b, c, d }
| 0 | a | b | c | d | e | |
|---|---|---|---|---|---|---|
| c | 0 | 0 | 0 | 1 | 0 | 0 |
| b | 0 | 0 | 1 | 0 | 0 | 0 |
| c | 0 | 0 | 0 | 2 | 0 | 0 |
| d | 0 | 0 | 0 | 0 | 3 | 0 |
| a | 0 | 1 | 0 | 0 | 0 | 0 |
动态规划:
由此可得出状态转移方程
DP[i][j] = DP[i - 1][j - 1] + 1;
伪码如下:
if(X[i] == Y[j])
DP[i][j] = d[i - 1][j - 1] + 1;
MaxValue = fmax(DP[i][j], MaxValue);
完整代码如下:
class Solution {
public:
int longestCommonSubsequence(string text1, string text2) {
int length1 = text1.length(), length2 = text2.length(), maxValue = 0;
vector<vector<int>> dp(length1 + 1, vector<int>(length2 + 1, 0));
for(int i = 1; i < length1 + 1; i++)
{
for(int j = 1; j < length2 + 1; j++)
{
if(text1[i - 1] == text2[j - 1])
dp[i][j] = dp[i - 1][j - 1] + 1;
maxValue = max(maxValue, dp[i][j]);
}
}
return maxValue;
}
};
关于子序列问题的总结
两种思路
1、第一种思路模板是一个一维的 dp 数组
int n = array.length;
int[] dp = new int[n];
for (int i = 1; i < n; i++) {
for (int j = 0; j < i; j++) {
dp[i] = 最值(dp[i], dp[j] + ...)
}
}
比如上面的最长递增子序列
DP的定义:在子数组 array[0…i] 中,我们要求的子序列(最长递增子序列)的长度是 dp[i]
1、第二种思路模板是一个二维的 dp 数组
int n = arr.length;
int[][] dp = new dp[n][n];
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (arr[i] == arr[j])
dp[i][j] = dp[i][j] + ...
else
dp[i][j] = 最值(...)
}
}
这种思路运用相对更多一些,尤其是涉及两个字符串/数组的子序列,比如前文讲的「最长公共子序列」。本思路中 dp 数组含义又分为「只涉及一个字符串」和「涉及两个字符串」两种情况。
2.1 涉及两个字符串/数组时(比如最长公共子序列),dp 数组的含义如下:
在子数组 arr1[0…i] 和子数组 arr2[0…j] 中,我们要求的子序列(最长公共子序列)长度为 dp[i][j]。
2.2 只涉及一个字符串/数组时(比如本文要讲的最长回文子序列),dp 数组的含义如下:
在子数组 array[i…j] 中,我们要求的子序列(最长回文子序列)的长度为 dp[i][j]。
第一种情况可以参考这两篇旧文:「编辑距离」「公共子序列」
下面就借最长回文子序列这个问题,详解一下第二种情况下如何使用动态规划。
Github 高start 算法总结 : https://labuladong.gitbook.io/