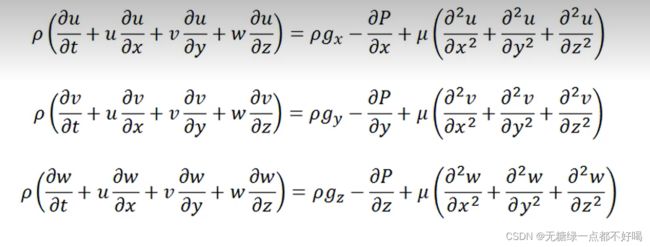2022.03.26 学习周报

---

摘要

This week, I read a computer science related to sequential recommendation systems; With the revival of neural networks, many studies have attempted to apply recurrent neural networks to the field of sequential recommendation, RNN-based networks encode historical interaction records as hidden state vectors; Although the encoding of state vectors can encode sequence dependencies, it has limited expressive power in capturing complex user preferences; To solve these problems, this computer science proposes a new knowledge enhancement sequential recommender; The model combines RNN-based networks with key value Memory networks (KV-MN), and further combines knowledge base (KB) information to enhance semantic representation, making the model highly interpretable. In addition, I learn about ant colony algorithm, LLE algorithm, and Navier-Stokes equation; For the learning of ant colony algorithm, I understand the core of the algorithm from the perspective of ideas, principles, mathematical models, and the implementation process of the algorithm; For the learning of the LLE algorithm, I try to implement the LLE algorithm using Python. By reducing the dimensions of the swiss roll dataset and comparing the results with those achieved by sklearn, the results are basically consistent; For the learning of Navier-Stokes equations, I try to conduct a simple mathematical derivation through Newton’s second law, further deepening my understanding of Navier-Stokes equations.

本周，我阅读了一篇与顺序推荐系统相关的文章；随着神经网络的复兴，许多研究试图将循环神经网络应用到顺序推荐领域中，基于RNN的网络会将历史交互记录编码为隐藏的状态向量；尽管状态向量的编码可以编码顺序依赖性，但它在捕捉复杂的用户偏好方面存在表示能力有限的情况；为了解决这些问题，文章提出了一种新的知识增强顺序推荐器；模型将基于RNN的网络与关键键值记忆网络(KV-MN)相结合，并且进一步结合知识库(KB)信息来增强语义表示，使得模型具有高度的可解释性。此外，我学习了蚁群算法、LLE算法和Navier-Stokes方程这三方面的内容；对于蚁群算法的学习，我从思想、原理、数学模型以及算法的实现流程去理解算法的核心；对于LLE算法的学习，我尝试用python去实现LLE算法，通过对swiss roll数据集降维，并与sklearn实现的效果进行对比，结果表现基本一致；对于Navier-Stokes方程的学习，我尝试通过牛顿第二定律进行一个简单的数学推导，对Navier-Stokes方程的理解得到进一步加深。

---

文献阅读

1.题目

文献链接：Improving Sequential Recommendation with Knowledge-Enhanced Memory Networks

2.摘要

With the revival of neural networks, many studies try to adapt powerful sequential neural models, i.e., Recurrent Neural Networks (RNN), to sequential recommendation. RNN-based networks encode historical interaction records into a hidden state vector. Although the state vector is able to encode sequential dependency, it still has limited representation power in capturing complicated user preference. It is difficult to capture fine-grained user preference from the interaction sequence. Furthermore, the latent vector representation is usually hard to understand and explain.
To address these issues, in this paper, we propose a novel knowledge enhanced sequential recommender. Our model integrates the RNN-based networks with Key-Value Memory Network (KV-MN). We further incorporate knowledge base (KB) information to enhance the semantic representation of KV-MN. RNN-based models are good at capturing sequential user preference, while knowledge enhanced KV-MNs are good at capturing attribute-level user preference. By using a hybrid of RNNs and KV-MNs, it is expected to be endowed with both benefits from these two components. The sequential preference representation together with the attribute-level preference representation are combined as the final representation of user preference. With the incorporation of KB information, our model is also highly interpretable. To our knowledge, it is the first time that sequential recommender is integrated with external memories by leveraging large-scale KB information.

3.介绍

3.1 背景

随着深度学习的发展，人们探索出了一系列的方法来处理序列化数据，其中RNN被广泛使用。但是对于序列化推荐来说，RNN的处理方式存在不足，如其最后隐向量的编码很难理解，并且很难学习到用户细粒度的偏好；如不知道用户到底喜欢商品的哪个属性，是价格、质量、还是性价比。

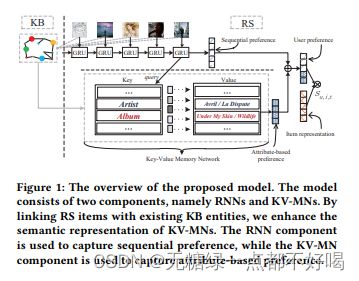
为了解决这个问题，作者提出一个带有键值对记忆网络的RNN模型架构。其中RNN用于捕捉序列化的用户偏好，而键值对记忆网络用于捕捉商品属性级的用户偏好，这两个向量组合在一起作为最终的用户偏好表示，从而解决了这个问题。

3.2 重点内容

1）随着Web技术的快速发展，推荐系统在将用户需求与各种在线平台的丰富资源相匹配方面发挥着越来越重要的作用；
2）在更多情况下，NCF和CKE能更好地执行BPR。因为NCF结合了一种神经结构来表征任意的user-item交互，而CKE利用知识库嵌入作为附加信号来增强稀疏用户-项目互动的建模；
3）作者发现项目级变体RUMI总体上比特征级RUMF表现得更好；
4）作者提出通过将基于门控递归单元的顺序推荐器与知识增强的KV内存网络集成来扩展它；
5）虽然只是在三个域和四个数据集上进行了实验，但作者相信自己的方法能适用于更多的域；
6）非结构化数据或者有噪声的上下文信息比格式良好的知识库信息更容易获得到，因此作者将考虑利用这种弱信号来扩展模型。

4.模型定义

U表示用户集合，I表示items集合，将用户与item的交互按照时间排序，得到{iu1, … itu, …, iun}，其中iut代表在t时刻与u交互的item，然后将item与KG结合起来。

任务：给定交互序列{iu1, … itu, …, iun}，然后去预测user会在n+1时刻点击的item。

5.模型结构

5.1 Augmenting Sequential Recommender with Knowledge-Enhanced Memory Networks

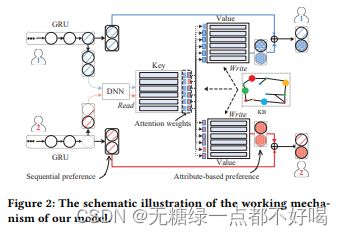
假设对所有item来说，它们具有相同的属性。比如：电影都具有演员、导演、上映时间等属性，这样网络就可以被概括为一个数组，其中key代表某一个属性，而value代表这个属性的值。这里需要注意的是，value的值是与用户相关的，即不同用户具有不同的value，但是因为所有item具有相同的属性，因此key对于所有用户来说是共享的。这个相当于对一个用户来说，他对某一个属性具有自己的用户偏好。

key值是经过预处理的，在整个训练过程中保持不变。采用transE的方式，我们可以得到KG中entiey和relation的embedding。作者认为entity的属性是与relation的含义相关的，因此我们直接将relation embedding作为key值，Ka = ra，其中a指某一个属性。

记忆网络涉及两个操作，read和write。read操作是从记忆网络读出value，然后经过一系列运算得到，用户u在t时刻从记忆网络得到的值，即GRU的输出。read可概括为：


write操作是指每当新的交互item到来之后，value矩阵必须更新，可概括为:


ea^ i是指item到来之后，对a属性value值的更新。之所以选择将ei + ra的结果作为 ea^i，是因为item在某个属性上的取值可能有多个。

5.2 The Complete Sequential Recommender

为了充分利用item的辅助信息，我们采用qi hat = qi + ei 编码item，最后分数计算采用(MLP 多层感知机，目的是将Ptu和qi hat映射到相同空间)：

采用BPR loss，AdaGrad优化策略：

6.实验

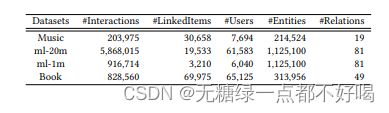
6.1 数据集

性能评价指标：MAP, MRR, HR, NDCG

6.2 Baseline

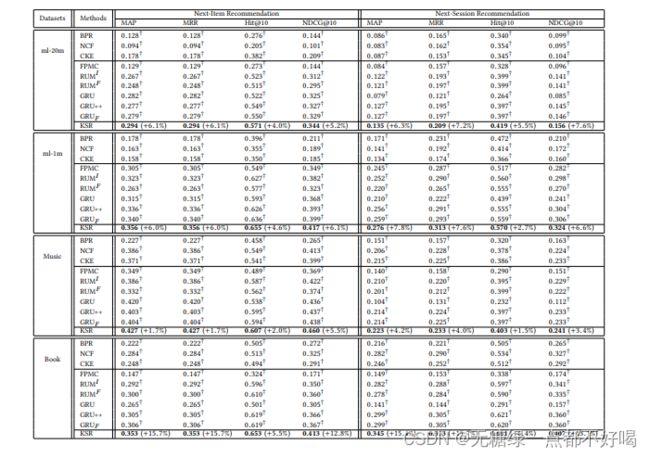
6.3 实验结果

实验结果表明，在每个数据集上都取得了不错的提升：

6.4 对比分析实验

1）数据集大小对实验结果的影响：

2）是否共享键值记忆网络的值矩阵对实验结果的影响：

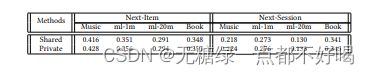
3）不同的KG embedding方式和选择的向量维度对实验结果的影响：

7.结论

1）通过将基于GRU的顺序推荐器与知识增强的KV-MNs集成来扩展，使得模型具有这两个组成部分的优点；
2）通过启发式地将RS项目与现有的知识库实体联系起来，作者利用大规模的知识库信息来改进顺序推荐；
3）作者从RS和KBs中构建了四个大型链接数据集，结果表明该模型在有效性和可解释性方面优于此前的方法；
4）非结构化数据或有噪声的上下文信息比格式良好的KB信息更容易获得，作者将考虑利用这种弱信号来扩展模型。

蚁群算法

1.基本思想

蚁群算法的基本原理来源于自然界中蚂蚁觅食的最短路径问题，其实蚂蚁的视觉并不敏感，但是它们可以在没有任何提示的情况下找到食物到巢穴的最短路径，即使出现一些情况，如原来路径上出现了路障，蚂蚁都可以自适应地找到新的最佳路径。

蚂蚁在寻找食物的过程中，会在其走过的路径上释放一种蚂蚁特有的分泌物（信息素），使得一定范围内的其他蚂蚁能够察觉到并且影响到它们后面的行为。当一些路径上通过的蚂蚁越来越多时，其留下的信息素也越来越多，导致信息素强度增大，所以蚂蚁选择该路径的概率也越高，这种选择过程是一种正反馈过程。其中，随着时间的推移，信息素强度也会逐渐减弱。

2.基本原理

1）蚂蚁携带等量的信息素在周游过程中释放；
2）信息素的浓度和路径的长度成反比；
3）蚂蚁利用信息素进行相互通信，下次蚂蚁来到路口会选择信息素浓度较高的那条路；
4）短的路径上的信息素浓度会越来越大，最终成为蚁群的最优路径，即产生最优解。

3.数学模型

用蚁群算法求解TSP问题，并建立相应的数学模型：
1）设整个蚂蚁群体中蚂蚁的数量为m，城市的数量为n，城市i与城市j之间的距离为dij(i, j=1, 2, …, n)，t时刻城市i与城市j连接路径上的信息素浓度为rij(t)；初始时刻，蚂蚁被放置在不同的城市里，且各城市间连接路径上的信息素浓度相同，设rij(0) = r(0)；然后蚂蚁按一定概率选择线路，而TSP策略会受到访问某城市的期望和其他蚂蚁释放的信息素浓度两方面的影响：

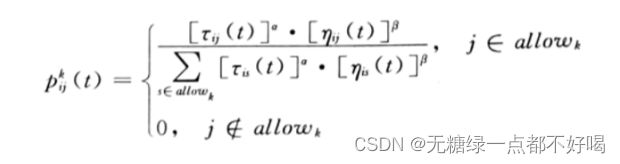
其中：α，β越大，则代表对信息素浓度和访问某城市的期望影响越大。

2）信息素强度会随着时间的推移逐渐减弱，因此用 ρ 表示信息素的挥发程度，即可以得到各个城市间连接路径上的信息浓度为：

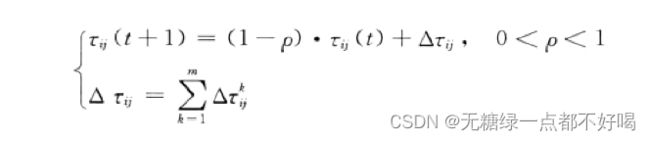
其中：△r^k (ij) 表示第k只蚂蚁在城市i与城市j连接路径上释放信息素，而增加的信息素浓度；△rij 表示所有蚂蚁在城市i与城市j连接路径上释放信息素，而增加的信息素浓度。

3）蚂蚁k在路径上释放信息素，而增加的信息素浓度可表示为：

其中：Q表示蚂蚁循环一次所释放的信息素总量；Lk表示第k只蚂蚁经过路径的总长度。

4.算法流程

用蚁群算法求解TSP问题的算法流程：
1）对相关参数进行初始化，将数据读入程序，并对数据进行基本的处理；
2）随机将蚂蚁放于不同的出发点，对每个蚂蚁计算其下一个访问城市，直至所更新信息素表有蚂蚁访问完所有城市；
3）计算各个蚂蚁经过的路径长度 Lk，记录当前迭代次数中的最优解，同时对各个城市连接路径上的信息素浓度进行更新；
4）判断是否达到最大迭代次数，若否，则返回步骤2，否则终止程序；
5）输出程序结果，并根据需要输出程序寻优过程中的相关指标。

5.算法实现

import numpy as np
import matplotlib.pyplot as plt


# 建立“蚂蚁”类
class Ant(object):
    def __init__(self, path):
        self.path = path  # 蚂蚁当前迭代整体路径
        self.length = self.calc_length(path)  # 蚂蚁当前迭代整体路径长度

    def calc_length(self, path_):  # path=[A, B, C, D, A]注意路径闭环
        length_ = 0
        for i in range(len(path_) - 1):
            delta = (path_[i].x - path_[i + 1].x, path_[i].y - path_[i + 1].y)
            length_ += np.linalg.norm(delta)
        return length_

    @staticmethod
    def calc_len(A, B):  # 静态方法，计算城市A与城市B之间的距离
        return np.linalg.norm((A.x - B.x, A.y - B.y))


# 建立“城市”类
class City(object):
    def __init__(self, x, y):
        self.x = x
        self.y = y


# 建立“路径”类
class Path(object):
    def __init__(self, A):  # A为起始城市
        self.path = [A, A]

    def add_path(self, B):  # 追加路径信息，方便计算整体路径长度
        self.path.append(B)
        self.path[-1], self.path[-2] = self.path[-2], self.path[-1]


# 构建“蚁群算法”的主体
class ACO(object):
    def __init__(self, ant_num=50, maxIter=300, alpha=1, beta=5, rho=0.1, Q=1):
        self.ants_num = ant_num  # 蚂蚁个数
        self.maxIter = maxIter  # 蚁群最大迭代次数
        self.alpha = alpha  # 信息启发式因子
        self.beta = beta  # 期望启发式因子
        self.rho = rho  # 信息素挥发速度
        self.Q = Q  # 信息素强度

        self.deal_data('../data/coordinates.dat')  # 提取所有城市的坐标信息

        self.path_seed = np.zeros(self.ants_num).astype(int)  # 记录一次迭代过程中每个蚂蚁的初始城市下标
        self.ants_info = np.zeros((self.maxIter, self.ants_num))  # 记录每次迭代后所有蚂蚁的路径长度信息
        self.best_path = np.zeros(self.maxIter)  # 记录每次迭代后整个蚁群的“历史”最短路径长度

        self.solve()  # 完成算法的迭代更新
        self.display()  # 数据可视化展示

    def deal_data(self, filename):
        with open(filename, 'rt') as f:
            temp_list = list(line.split() for line in f)  # 临时存储提取出来的坐标信息
        self.cities_num = len(temp_list)  # 1. 获取城市个数
        self.cities = list(City(float(item[0]), float(item[1])) for item in temp_list)  # 2. 构建城市列表
        self.city_dist_mat = np.zeros((self.cities_num, self.cities_num))  # 3. 构建城市距离矩阵
        for i in range(self.cities_num):
            A = self.cities[i]
            for j in range(i, self.cities_num):
                B = self.cities[j]
                self.city_dist_mat[i][j] = self.city_dist_mat[j][i] = Ant.calc_len(A, B)
        self.phero_mat = np.ones((self.cities_num, self.cities_num))  # 4. 初始化信息素矩阵
        # self.phero_upper_bound = self.phero_mat.max() * 1.2                              ###信息素浓度上限
        self.eta_mat = 1 / (self.city_dist_mat + np.diag([np.inf] * self.cities_num))  # 5. 初始化启发函数矩阵

    def solve(self):
        iterNum = 0  # 当前迭代次数
        while iterNum < self.maxIter:
            self.random_seed()  # 使整个蚁群产生随机的起始点
            delta_phero_mat = np.zeros((self.cities_num, self.cities_num))  # 初始化每次迭代后信息素矩阵的增量

            for i in range(self.ants_num):
                city_index1 = self.path_seed[i]  # 每只蚂蚁访问的第一个城市下标
                ant_path = Path(self.cities[city_index1])  # 记录每只蚂蚁访问过的城市
                tabu = [city_index1]  # 记录每只蚂蚁访问过的城市下标，禁忌城市下标列表
                non_tabu = list(set(range(self.cities_num)) - set(tabu))
                for j in range(self.cities_num - 1):  # 对余下的城市进行访问
                    up_proba = np.zeros(self.cities_num - len(tabu))  # 初始化状态迁移概率的分子
                    for k in range(self.cities_num - len(tabu)):
                        up_proba[k] = np.power(self.phero_mat[city_index1][non_tabu[k]], self.alpha) * \
                                      np.power(self.eta_mat[city_index1][non_tabu[k]], self.beta)
                    proba = up_proba / sum(up_proba)  # 每条可能子路径上的状态迁移概率
                    while True:  # 提取出下一个城市的下标
                        random_num = np.random.rand()
                        index_need = np.where(proba > random_num)[0]
                        if len(index_need) > 0:
                            city_index2 = non_tabu[index_need[0]]
                            break
                    ant_path.add_path(self.cities[city_index2])
                    tabu.append(city_index2)
                    non_tabu = list(set(range(self.cities_num)) - set(tabu))
                    city_index1 = city_index2
                self.ants_info[iterNum][i] = Ant(ant_path.path).length
                if iterNum == 0 and i == 0:  # 完成对最佳路径城市的记录
                    self.best_cities = ant_path.path
                else:
                    if self.ants_info[iterNum][i] < Ant(self.best_cities).length: self.best_cities = ant_path.path
                tabu.append(tabu[0])  # 每次迭代完成后，使禁忌城市下标列表形成完整闭环
                for l in range(self.cities_num):
                    delta_phero_mat[tabu[l]][tabu[l + 1]] += self.Q / self.ants_info[iterNum][i]

            self.best_path[iterNum] = Ant(self.best_cities).length

            self.update_phero_mat(delta_phero_mat)  # 更新信息素矩阵
            iterNum += 1

    def update_phero_mat(self, delta):
        self.phero_mat = (1 - self.rho) * self.phero_mat + delta
        # self.phero_mat = np.where(self.phero_mat > self.phero_upper_bound, self.phero_upper_bound, self.phero_mat)
        # 判断是否超过浓度上限

    def random_seed(self):  # 产生随机的起始点下表，尽量保证所有蚂蚁的起始点不同
        if self.ants_num <= self.cities_num:  # 蚂蚁数 <= 城市数
            self.path_seed[:] = np.random.permutation(range(self.cities_num))[:self.ants_num]
        else:  # 蚂蚁数 > 城市数
            self.path_seed[:self.cities_num] = np.random.permutation(range(self.cities_num))
            temp_index = self.cities_num
            while temp_index + self.cities_num <= self.ants_num:
                self.path_seed[temp_index:temp_index + self.cities_num] = np.random.permutation(range(self.cities_num))
                temp_index += self.cities_num
            temp_left = self.ants_num % self.cities_num
            if temp_left != 0:
                self.path_seed[temp_index:] = np.random.permutation(range(self.cities_num))[:temp_left]

    def display(self):  # 数据可视化展示
        plt.figure(figsize=(6, 10))
        plt.subplot(211)
        plt.plot(self.ants_info, 'g.')
        plt.plot(self.best_path, 'r-', label='history_best')
        plt.xlabel('Iteration')
        plt.ylabel('length')
        plt.legend()
        plt.subplot(212)
        plt.plot(list(city.x for city in self.best_cities), list(city.y for city in self.best_cities), 'g-')
        plt.plot(list(city.x for city in self.best_cities), list(city.y for city in self.best_cities), 'r.')
        plt.xlabel('x')
        plt.ylabel('y')
        plt.savefig('ACO.png', dpi=500)
        plt.show()
        plt.close()


ACO()

b站讲解视频链接：https://www.bilibili.com/video/BV1cR4y1W7qT?p=2&vd_source=15153815a2ec96bae8286f64ac6083b7

LLE

python实现LLE算法：

import numpy as np
from sklearn.datasets import make_s_curve
import matplotlib.pyplot as plt
from sklearn.manifold import LocallyLinearEmbedding
from mpl_toolkits.mplot3d import Axes3D


# 1.生成swiss roll数据集
def make_swiss_roll(n_samples=100, noise=0.0):
    t = 1.5 * np.pi * (1 + 2 * np.random.rand(1, n_samples))
    x = t * np.cos(t)
    y = 83 * np.random.rand(1, n_samples)
    z = t * np.sin(t)
    X = np.concatenate((x, y, z))
    X += noise * np.random.rand(3, n_samples)
    X = X.T
    t = np.squeeze(t)
    return X, t


# 2.计算两点间的距离
# (a - b)^2 = a^2 + b^2 - 2*a*b
def cal_pairwise_dist(x):
    sum_x = np.sum(np.square(x), 1)
    dist = np.add(np.add(-2 * np.dot(x, x.T), sum_x).T, sum_x)
    return dist


# 3.找样本点的n个邻近点
def get_n_neighbors(data, n_neighbors=10):
    dist = cal_pairwise_dist(data)
    dist[dist < 0] = 0
    n = dist.shape[0]
    N = np.zeros((n, n_neighbors))

    for i in range(n):
        index_ = np.argsort(dist[i])[1:n_neighbors + 1]
        N[i] = N[i] + index_

    return N.astype(np.int32)


# 4.LLE算法，重构低维数据
def LLE(data, n_dims=2, n_neighbors=10):
    N = get_n_neighbors(data, n_neighbors)
    n, D = data.shape

    # 防止Si变小
    if n_neighbors > D:
        tol = 1e-3
    else:
        tol = 0

    # 计算W
    W = np.zeros((n_neighbors, n))
    I = np.ones((n_neighbors, 1))
    for i in range(n):
        Xi = np.tile(data[i], (n_neighbors, 1)).T
        Ni = data[N[i]].T

        Si = np.dot((Xi - Ni).T, (Xi - Ni))

        Si = Si + np.eye(n_neighbors) * tol * np.trace(Si)

        Si_inv = np.linalg.pinv(Si)
        wi = (np.dot(Si_inv, I)) / (np.dot(np.dot(I.T, Si_inv), I)[0, 0])
        W[:, i] = wi[:, 0]

    print("Xi.shape", Xi.shape)
    print("Ni.shape", Ni.shape)
    print("Si.shape", Si.shape)

    W_y = np.zeros((n, n))
    for i in range(n):
        index = N[i]
        for j in range(n_neighbors):
            W_y[index[j], i] = W[j, i]

    I_y = np.eye(n)
    M = np.dot((I_y - W_y), (I_y - W_y).T)

    eig_val, eig_vector = np.linalg.eig(M)
    index_ = np.argsort(np.abs(eig_val))[1:n_dims + 1]
    print("index_", index_)
    Y = eig_vector[:, index_]
    return Y


if __name__ == '__main__':
    X, Y = make_swiss_roll(n_samples=500, noise=0.1)

    data_1 = LLE(X, n_neighbors=30)
    print(data_1.shape)

    data_2 = LocallyLinearEmbedding(n_components=2, n_neighbors=30).fit_transform(X)

    plt.figure(figsize=(8, 4))

    plt.subplot(121)
    plt.title("my_LLE")
    plt.scatter(data_1[:, 0], data_1[:, 1], c=Y)

    plt.subplot(122)
    plt.title("sklearn_LLE")
    plt.scatter(data_2[:, 0], data_2[:, 1], c=Y)

    plt.savefig("LLE.png")
    plt.show()

生成swiss roll数据集：

查看输出：

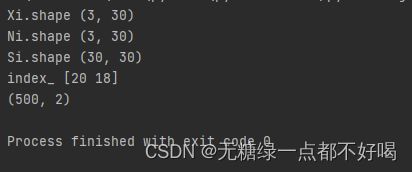
与sklearn实现的效果进行对比：

b站讲解视频链接：https://www.bilibili.com/video/BV14g411F7Je/?spm_id_from=333.337.search-card.all.click&vd_source=15153815a2ec96bae8286f64ac6083b7

Navier-Stokes方程

1.Navier-Stokes方程的通常写法

2.根据牛顿第二定律进行简单的数学推导

1）外力的总和等于质量乘以加速度：
ΣFx = m *ax
ΣFy = m *ay
ΣFz = m *az
这些方程表示流体的一个微元，它无穷小，小到我们难以想象。
2）我们所关心的外力是重力导致的外力，压力差导致的外力以及流体粘性导致的外力（以单位体积计算）：

方程左边：mg/v = ρg；方程右边：ma/v = ρa
3）以X方向推导为例：

同理，可以把Y，Z方向推导出来：

4）将推导出的方程变成Navier-Stokes方程：
现在要将常规压力和剪应力和流体的黏度和速度剖面关联起来，可以通过牛顿流体的本构关系，使用这些方程实现。

以X方向推导为例（需要用到连续性方程）：

Y，Z方向同理可得，联立三个方程即可得到我们常见的Navier-Stokes方程：

---

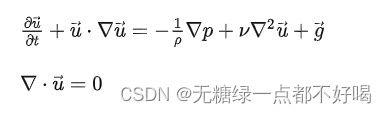
总结

对于LLE算法的学习，我补充学习了用python实现LLE算法，并与sklearn实现的效果进行对比，最后得到效果比较不错；对于Navier-Stokes方程的学习，我们可以通过牛顿第二定律进行简单的数学推导，因为方程可以看作是外力的总和等于质量乘以加速度；对于蚁群算法的学习，我基本掌握了蚁群算法的原理以及建立相应的数学模型，但是蚁群算法的代码实现方面还没能理解清楚。下周，我将学习新的降维方法，机器学习相关知识以及进一步理解Navier-Stokes方程。