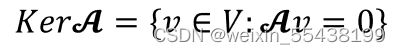数据分析-统计基础
集中趋势，离散测度，均值，中位数，众数，方差等点估计，区间估计等相关的知识
一：基与坐标
1.1基
基的定义：向量空间的一组基是张成该空间的一个线性无关的向量组。
例如，在2空间中，最常用的一组基就是自然基（i,j），其中i=
，j=
，显然，2中所有向量都可以通过他们的线性组合线性表出，且这两个向量线性无关。
1.2坐标
坐标的定义：向量可以被基1,2,…,唯一地线性表出：
=11+22+…+
则系数1,2,…,称为向量在基1,2,…,下的坐标，记为(1,2,…,)
一个向量 在不同的基下 坐标一般也不同。
二：线性变换与矩阵
2.1线性变换（也称线性映射）
从空间V到V的线性变换是对加法和数乘封闭的函数 :→T:V→V
也就是说，空间V中的任意一个元素，都可以通过变换T从V中找到另一个元素与之一一对应。
变换一个向量有两种方式：
线性空间中，改变空间只需改变基，也就是改变基向量的方向和长度。线性变换通常用大写花体字母表示，例如 ,
2.2矩阵
矩阵代表一次变换。用一个向量左乘一个矩阵，就表示将这个向量按此矩阵所定义的变换映射到新的向量。（矩阵一般用大写英文字母表示，例如 A, B）
矩阵乘法（矩阵乘法就是复合变换：两个变换先后作用）
矩阵乘法的规则：行和列分别相乘
三：行列式
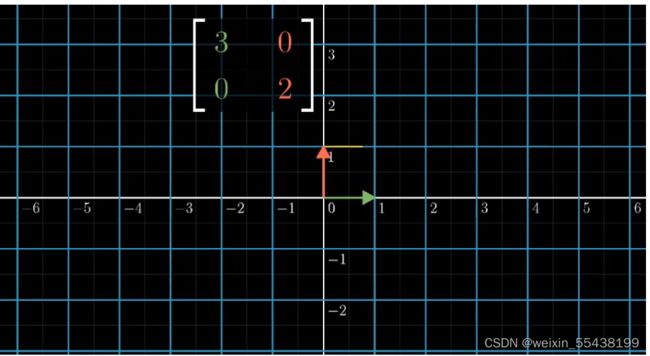
以2维空间为例：
既然线性变换是改变基组，那么我们只需要找到一个指标来度量 2个基向量围成的矩形面积 增大或缩小的比例。
该指标就是行列式的值。记作det()，或| |
例：
行列式计算规则：主对角线相乘减去副对角线相乘
行列式总结：1.若行列式的值为负，表示空间发生了翻转，交换了坐标轴的顺逆时针顺序 2.矩阵行列式等于零，则矩阵一定出现了向量的线性相关，则空间一定会被降维 3.行类式行数必须等于列数，也就是说必须式方阵才有行列式
四：逆矩阵和矩阵的秩
在线性代数里，当det(A)=0时，空间被降维后就没有对应的逆变换−1A^(-1)能变回去了。
因此当det(A)=0，逆不存在。
不可逆矩阵称为奇异矩阵。
可逆矩阵称为非奇异矩阵
4.2单位矩阵
在所有矩阵中主对角线元素为1，其他元素都为0的矩阵，就代表什么都不做的变换。
这种矩阵称为单位矩阵，记作I或者E.
4.3核
所有被线性变换变成零向量的向量组成的集合，称为该变换的“核”
在几何上，核就是即将在变换后落在原点的向量的集合。
4.4值域
所有被线性变换映射出的向量的集合，称为该变换的“值域”，就是