【论文笔记_剪枝_知识蒸馏_2022】INDISTILL: TRANSFERRING KNOWLEDGE FROM PRUNED INTERMEDIATE LAYERS

摘要

在资源有限的硬件上部署深度神经网络，如智能手机和无人机，由于其计算复杂性，构成了巨大的挑战。知识提取方法旨在将知识从大型模型转移到轻量级模型，也分别称为教师和学生，而从中间层提取知识为该任务提供了额外的监督。模型之间的容量差距、破坏其架构一致性的信息编码以及缺乏用于转移多层的适当学习方案限制了现有方法的性能。在本文中，我们提出了一种新的方法，称为InDistill，它可以通过利用通道剪枝的属性来显著提高现有单层知识提取方法的性能，以减少模型之间的容量差距并保持体系结构的一致性。此外，我们提出了一个基于课程学习的方案，以提高从多个中间层转移知识的有效性。所提出的方法在三个基准图像数据集上超过了最先进的性能。

1.介绍

在过去的十年中，深度神经网络已经被成功地应用于广泛的领域。由于DNN能够在各种任务上实现最先进的性能，因此不断提高其性能的努力导致了需要大量计算能力的更深入的dnn，这限制了它们在资源有限的硬件中的部署，例如移动设备。这使得研究团体将注意力集中在能够克服这一关键限制的方法上。知识蒸馏(KD)方法是解决这一障碍的最有效的方法之一[1，2]。KD方法的基本思想是将DNN(即教师模型)拥有的有价值的知识转移到更小更快的网络(即学生模型)中，从而提高其性能。

早期知识发现方法的主要目标是将来自教师网络最后一层的知识转移到相应的学生网络最后一层[3]。这使得较小的模型能够理解较大的模型如何感知训练数据，从而提高它们的泛化能力和性能。出于同样的想法，最近的几种知识发现方法[4，5，6]不仅关注于利用教师的最后一层，而且还关注于利用它的中间层来为学生模型提供更丰富的信息源，这些信息源可以帮助学生模型进一步提高其准确性。事实上，中间层KD通过提供一些关于信息如何流入教师模型的主要信息，作为最后一层KD的补充。虽然这种额外的监督确实提高了学生的成绩，有两个主要的缺点应该加以考虑。第一个是教师和学生模型之间的能力差距，这在传递知识时导致溢出，并且作为一个序列降低了知识发现的有效性。第二个挑战是同时从多个层面传递知识。注意，在训练过程中，神经网络经历几个阶段。Achille等人[7]认为，第一个训练时期负责创建模型的信息流路径，这是中间层知识发现方法的目标关键信息。

在本文中，我们提出了一种新的中间层知识发现方法，称为InDistill，旨在克服上述局限性。首先，应该强调的是，中间层KD问题的性质(即，提取关于关键连接的基础知识)允许在不破坏感兴趣的信息的情况下减少容量差距。鉴于此，我们认为修剪教师中间层的输出通道可以有效地减少教师和学生之间的能力差距，同时保持教师的基本知识。通道修剪方法被广泛应用于通过移除冗余输出通道来降低模型的复杂性[8]。据我们所知，这是第一个利用通道修剪来应用中间层KD的工作。此外，适当设计的教师通道修剪可以允许匹配教师和学生模型的特征图大小，从而实现直接知识转移，这对于保持网络的架构宽度方向对齐也是至关重要的。保持这种一致性对于获取网络的信息流路径至关重要。值得注意的是，所提出的方法可以与任何单层KD方法相结合以提高其性能。其次，受课程学习策略[9]的启发，我们提出了一种简单而有效的方法来提取从教师到学生模型的多个层次，同时考虑到关键学习阶段[4]，称为基于分层课程学习的方案(l-CLS)。具体来说，我们建议按照迁移难度从高到低的顺序(即从最容易的第一层到最难的最后一层)分别迁移每个中间层可以提高知识发现的有效性，从而提高学生的成绩。图1中示出了包括InDistill和l-CLS的所提出的方法。该代码可在https://github.com/gsarridis/InDistill.git.获得。

在分类和检索任务以及在CIFAR-10 [10]、CUB-200 [11]和FashionMNIST [12]数据集上对所提出的方法进行了评估，并证明了与几种最先进的方法相比的优越性能。具体来说，InDistill-l-CLS在CIFAR-10数据集上实现了1.61%的平均精度(mAP)相对改善，在CUB-200数据集上实现了3.59%的精度相对改善。此外，为了评估所提出的方法如何影响它们的性能，结合三个有竞争力的单层KD方法来说明所提出的方法的性能。本文的主要贡献如下:(1)通过在教师中间层上应用信道剪枝来减少教师和学生模型之间的容量差距。这样，我们的方法为学生模型学习教师的信息流路径提供了适当的监督。(ii)应用通道修剪可以减少教师的过滤器，使得它们匹配学生的过滤器的大小。因此，InDistill允许直接传递特征图，而不包括任何可能破坏架构对齐的编码过程(如其他方法所做的)( iii)引入基于课程学习的方案，该方案在考虑神经网络的临界学习周期的同时辅助多层传递过程。

2.相关工作

…

HIT方法[6]选择一个中间层来传输并利用回归量来匹配教师/学生的特征图大小。然而，传递一个中间层的知识并不能抓住各层之间的关键联系。为了缓解这一缺点，注意力转移(A T) [5]提出了一种转移中间层表示的注意力机制，但它也对特征图进行编码，以这种方式折叠它们的对齐。此外，概率知识转移(PKT) [21]通过匹配其概率分布来转移从倒数第二层(即，分类层之前的最后一层)提取的特征，而不利用任何其他中间层。在[22]中，作者介绍了一种在KD过程之前对提取的特征进行有效编码的方法。在[23]中，通过生成解决方案流程(FSP)矩阵来捕捉连续层之间的关系，从而努力捕捉信息流。在[24]中，作者介绍了对比表示提取(CRD ),它使用对比损失来提取特征图(从最后一个卷积层得出),而忽略了信息流路径的重要性。此外，分层自监督增强知识蒸馏(HSAKD) [25]在中间层的顶部使用分类器来监督KD过程，这也破坏了架构宽度方向的对齐。

前面提到的从中间层转移知识的方法都有相同的缺点。它们只能应用于具有相似结构的教师/学生对，它们在转移前对特征图进行编码（折叠对齐），它们忽略了模型之间的容量差距，并且它们面临着同时转移多层的挑战。关于容量差距，Mirzadeh等人[26]建议使用一个辅助模型，以减少教师和学生模型之间的复杂性 “距离”，但应该强调的是，在KD过程中，中间层没有被利用。基于同样的想法，[4]也使用了一个辅助模型来缓解架构上的限制。另外，[4]提出了一个临界期感知的权重衰减方案，在每个epoch后降低中间层KD的学习率，因为第一个训练epoch负责信息流路径的创建[7]。受这些思想的启发，我们还采用了一个辅助的教师模型来初步减少能力差距（在我们通过修剪其通道进一步减少差距之前），并使我们的方法能够应用于结构非常不同的教师/学生对。另外，与其他方法相反，我们的方法直接与教师/学生的特征图相匹配，防止了排列组合的崩溃。

此外，课程学习[27, 28]被多个领域的众多方法所利用[29, 30, 31, 32, 33] 。课程学习建议将一个困难的任务按难度顺序分成几个子任务。例如，[34]介绍了一个用于强化学习的师生课程学习框架，其中教师决定学生在每个训练步骤中应该接受的子任务，而[35]则提出按顺序学习任务以提高多任务学习的有效性。受课程学习策略和关键期意识需求的启发[4]，我们提出了一种学习方案，既克服了转移多层的限制，又考虑了学习阶段，以帮助学生形成与教师相同的关键联系。

3.方法策略

3.1问题表述
将知识从教师转移到学生模型的问题被表述如下。让X∈R^3×h×w表示输入，d(·)是教师模型，l=1…L_d是层的索引，T^(l)=d(X,l)∈R表示教师层的输出。因此，考虑一个具有L_g卷积层和S^(l)的输出的学生模型g(·)。除此之外，令q_t和q_s分别是教师和学生模型的类概率分布。鉴于此，单层KD的目标是匹配教师和学生的类概率分布，或者匹配他们相应的倒数第二层表示(即，T^(Ld)和S^(Lg))，而中间层KD通过匹配几个教师和学生的中间层对来提供对主目标的额外监督。在我们的方法中，我们还利用了如下定义的辅助模型。f(·)表示辅助模型，Lf表示卷积层数(这里Lf =Lg)，A^(l) = f(X，l) ∈ R，与学生模型相比，它的输出特征图具有双通道，n_f,l=2·n_g,l。另外，请注意h_f，l=h_g，l和w_f，l=w_g，l，因为网络共享内核大小。最后，辅助的类概率分布表示为q_a。
3.2通道剪枝
修剪是一种广泛应用的技术，通过丢弃冗余参数来减少DNN的存储需求或/和推理时间[36，37]。为此，非结构化权重修剪方法通过将不重要的权重连接的相应值设置为0来移除这些不重要的权重连接，从而显著降低存储需求[38]。这些方法的限制是模型的结构要保持与修剪之前相同，因此在推理时间方面没有改进。另一方面，结构化滤波器修剪方法[8，39，40，41，42]旨在移除卷积神经网络(CNN)中不太重要的滤波器，以减少模型的存储大小和时间要求。评估滤波器重要性的典型标准是l1范数或l2范数。这里，我们选择使用[8]中提出的方法，该方法基于l1范数应用结构化通道修剪。具体来说，分别让f_i ∈ R^ni×hi×wi表示输入特征，f_o∈ R^no×ho×wo表示层的输出特征。鉴于此，层的过滤器可以表示为F ∈ R^ni×no×k×k，其中k是内核大小。然后，修剪程序如Alg1中所述。
（算法1：通道修剪过程
1.输入：滤波器F和要修剪得滤波器的数量p。 输出：修建后的滤波器F‘
2.计算每个滤波器的L1范数：s_i=…
3.对向量s进行排序，修剪掉s中值最小的p个滤波器
4.返回更新后的滤波器F’）

值得注意的是，现有的KD方法都没有利用修剪来增强KD性能。然而，信道修剪方法的性质可能是KD有效性的一个贡献因素，因为它保持了对于表示信息流路径至关重要的体系结构宽度方向的对齐，同时减少了限制要传输的信息量的容量差距。InDistill利用通道修剪的这些关键特征来进一步提高学生的成绩，详见第4节。

3.3中间层知识蒸馏
提取模型中间层的知识只适用于共享体系结构特征的教师/学生模型。例如，假设教师模型是具有残差块的CNN，只有当学生模型也是基于残差的并且具有与教师相同数量的块时，中间层KD才有效[4，24]。如果我们回忆起中间层KD的目的，即使学生能够学习教师的信息流，那么如果教师和学生模型具有不同的体系结构，那么匹配它们的信息流路径的努力将会失败。考虑到这一点，[4]建议使用一个辅助教师，允许在异构模型上进行知识发现。

在本文中，我们建立了辅助模型的概念，以解决所讨论的问题，并初步减少教师和学生之间的能力差距[26]。具体地，我们设计辅助模型，其包括与学生相同数量的层，并且其每个中间层的输出通道是相应学生通道的两倍。然后，因为它已经在第二节中定义了。3.1，辅助设备的输出特征映射表示为A^(l) = f(X，l) ∈ R^2 ng，l×hf，l×wf，l^.在进行KD之前，将结构化通道修剪方法应用于每个辅助中间层，进一步缩小产能差距，而不破坏对齐，如我们在第3.2节中所分析的。应用Alg1之后，对每个p = n_g，l的层，修剪的l层的输出特征图将是P(l) ∈ R^{ng，l×hf，l×wf，l}。注意，在通道修剪之后，辅助的和学生的特征图大小完全相同，这允许直接的知识传递，而不包括任何可能破坏对齐的编码。模型特征图P(l)和S(l)之间的损失定义为:

其中k2表示l2范数。假设InDistill只应用于中间层，那么任何现有的KD方法都可以用于最后一层。如前所述，InDistill可以与任何KD方法结合使用，以增强其有效性。在使用Kullback-Leibler (KL)散度损失转移类别概率分布的原始KD方法[3]的情况下，假设u和v分别表示辅助和学生的对数，则辅助和学生的概率分布由下式定义

3.4学习计划

中间层KD作为主要单层KD过程的补充，向学生模型教授教师的信息流路径。这些路径是在第一个训练时期形成的，因此需要采用一种知道关键学习时期的学习方案[4]。受这一思想的启发，并考虑到同时学习多个层次的困难，我们提出了一个基于课程学习的方案，以促进多层知识发现并进一步提高学生的表现。
课程学习策略建议将主任务分成若干子任务，根据它们的难度，然后按照难度递增的顺序学习每个子任务来训练模型。鉴于中间层知识发现由几个任务(即，要转移的层)组成，我们提出了l-CLS，一种新的课程学习方案，提高了层转移的有效性。特别是，让L_g的层数，然后有L_g子任务。如果训练时期的数量是E，那么对应于每个子任务的时期的数量可以计算如下:

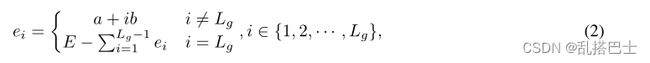
其中参数a表示每一层的训练时期的阈值，b是根据子任务的难度增加epoch数的参数。因此，对应于每个子任务的历元集定义为Si = { r_i-1+1，r_i-1+2，，ri}，i ∈ {1，2，，Lg}，其中：

采用l-CLS，第一个的epoch专用于中间层KD(即完全忽略最终任务)。通过这种方式，学生模型可以有效地形成重要的联系，这极大地促进了主要知识发现任务的完成，如第4部分所示。

4.实验设置

…

5.结果

…

6.结论

在本文中，我们介绍了一种新颖的中间层知识发现方法，该方法利用通道剪枝的特性来减少教师和学生模型之间的容量差距，并有效地捕获教师的信息流路径，这些路径对于中间层知识发现来说是最重要的。此外，我们提出了一个基于课程的学习方案，它简化了多层转换的过程，提高了主要知识发现过程的效率。所提出的方法已经针对不同的任务进行了评估，并且与几个有竞争力的单层KD方法相结合，成功地增强了它们的性能。这项工作的局限性可能是需要为每个不同的学生设计适当的辅助模型，以及多步KD方法比简单的KD方法在计算上要求更高的事实。