《排序算法篇》快排的递归与非递归

一、本章重点

1. 快排的思想

2. 实现单趟快排的三种方式（hoare、挖坑、前后指针）

3. 递归实现快排

4. 快排递归算法时间复杂度计算

5. 对快排进行优化（三数取中，小区间优化）

6. 非递归实现快排（栈或队列实现）

二、快排

2.1快排思想

快排本质上是一种交换排序，我们先从单趟的角度来说：快排的单趟排序会让你选择Key放在数组正确的位置，什么是正确的位置？就是你单趟排序后，这个数（Key）就已经排好了，后续不需要改变了，怎么保证它处于正确的位置呢？只要它的左边的所有数都小于等于它，右边的所有数都大于等于它，那么它就处于正确的位置。（升序）。

快排单趟步骤：从数组选择一个Key的数字，一般选择最左边或者最右边，这里我选择数组最左边的数，举例：5 3 2 8 6 1 10 9 3 4 7，这里的Keyi就是0,a[ keyi ]是5

如何进行交换数组元素让5放在正确的位置？

2.2三种单趟排序

这里有三种快排的单趟排序算法：

第一种：hoare，也是最早发明快速排序算法人写的-----托尼·霍尔（Tony Hoare）

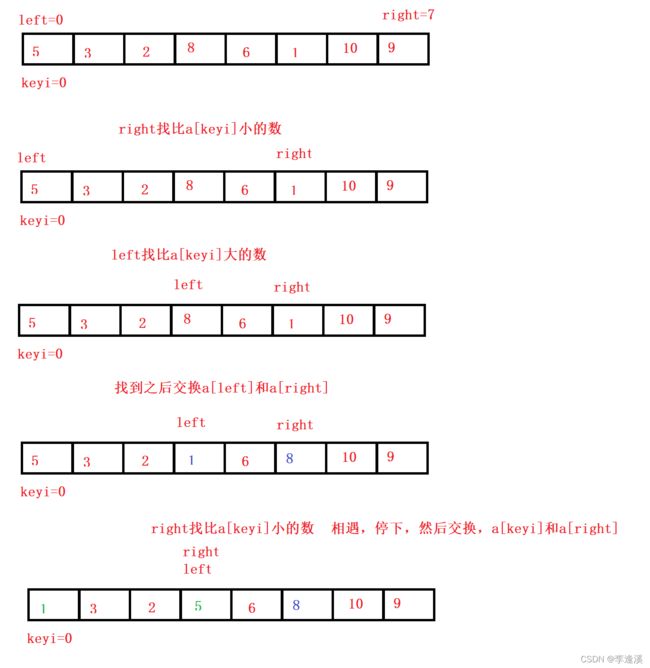
这种方法是：先选一个Keyi,取两个整形变量left、right，这两个整形变量代表数组下标，初始它们分别指向0和n-1。然后让right先移动，找到大于a[ keyi ]的数，然后right停下来，再让left移动，找到小于a[ keyi ]的数，停下，再交换a[ left ]和a[ right ]，如果在right或者left移动的途中，right==left，即right和left相遇的时候，right和left必然指向的是比a[ keyi ]小的数。然后a[keyi]和这个比它小的数交换（相遇点），它们最终a[keyi]处于正确位置，即它的左边所有数都小于等于它，右边所有数都大于等于它。

图示：

 需要注意的是：需让right先走，然后left在走。否则它们相遇点可能不是比a[keyi]小的数。

参考代码：

int Q_PartSort1(int* a, int begin, int end)//hoare
{
	int keyi = begin;
	int left = begin;
	int right = end;
	while (left < right)
	{
		while (left < right && a[right] >= a[keyi])//右边找小于a[keyi]的数
		{
			right--;
		}
		while (left < right && a[left] <= a[keyi])//左边找大于a[keyi]的数
		{
			left++;
		}
		Swap(&a[left], &a[right]);
	}
	//将a[keyi]与相遇点交换（要保证相遇点比a[keyi]小，需要让right先走）
	Swap(&a[keyi], &a[right]);
	return right;
}

第二种：挖坑法

步骤：先保存a[keyi]的值到int temp上，然后将keyi先作坑，int left=0、int right=n-1

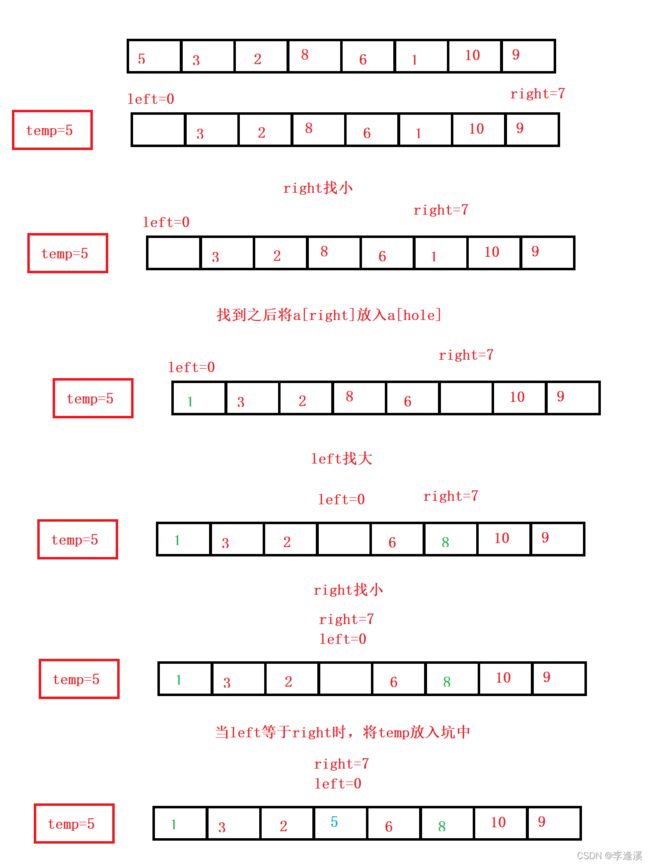
先让right走，找到小于a[keyi]的数，就将它放在a[hole]处，更新hole=right。然后left再走，找到大于a[keyi]的数，然后将它放在a[hole]处，再次更新hole=left，再让right移动，left移动，直到left等于right。此时相遇点必然是一个坑，最后将temp放在a[hole]处。

图示：

 与hoare不同的是这里并不需要保证相遇点的值比temp小。

参考代码：

int Q_PartSort2(int* a, int begin, int end)//挖坑法
{
	int key = a[begin];
	int hole = begin;
	int left = begin;
	int right = end;
	while (left < right)
	{
		while (left < right && a[right] >= key)
		{
			right--;
		}
		a[hole] = a[right];
		hole = right;
		while (left < right && a[left] <= key)
		{
			left++;
		}
		a[hole] = a[left];
		hole = left;
	}
	a[hole] = key;
	return hole;
}

第三种：前后指针法

取最左边的下标左keyi，prev=begin、next=begin+1

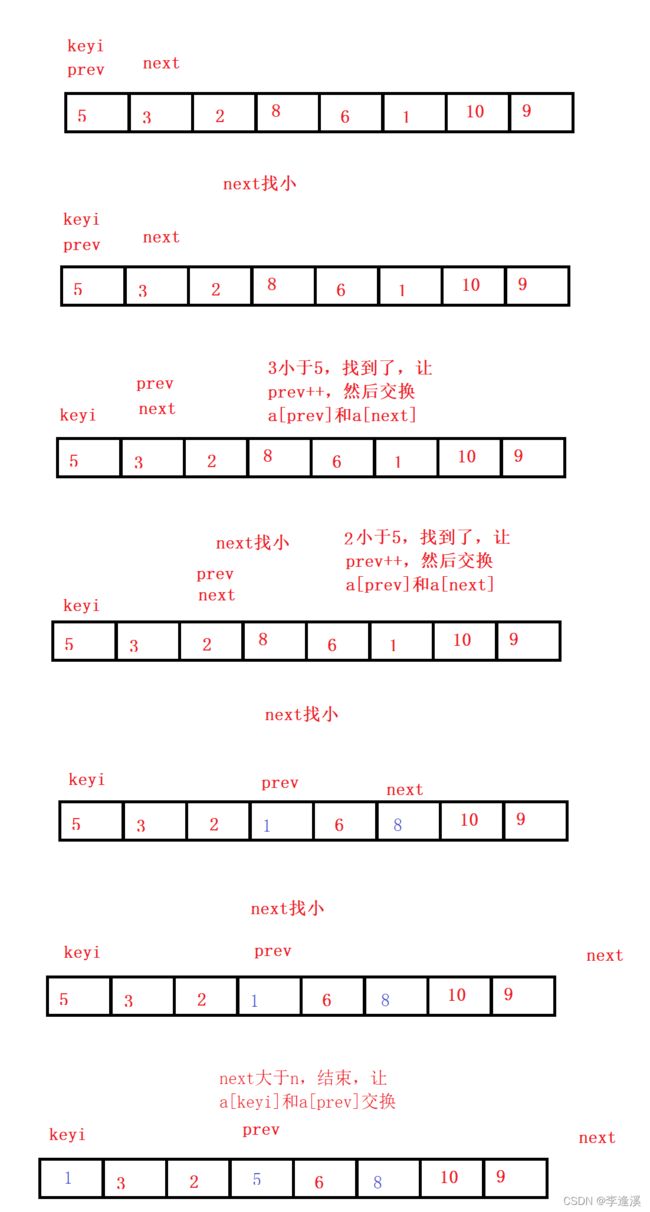
next找小，如果找到小于a[ keyi ]的数，就让prev++，然后将a[prev]和a[next]交换。

直到next大于n，结束。

最后再让a[keyi]和a[prev]交换。

图示：

 参考代码：

int Q_PartSort3(int* a, int begin, int end)//前后指针法
{
	int keyi = begin;
	int prev = begin;
	int next = begin + 1;
	while (next <= end)
	{
		if (a[next] < a[keyi] && ++prev != next)
		{
			Swap(&a[prev], &a[next]);
		}
		next++;
	}
	Swap(&a[keyi], &a[prev]);
	return prev;
}

三种单趟排序，我们都需要掌握，有的时候会考查下面这种题目

需要说明的是：上面这组数据虽然三种单趟排序之后结果是一样的，但这属于巧合情况，增加更多的数据，单趟之后结果可能会不同。

设一组初始记录关键字序列为(65,56,72,99,86,25,34,66)，则以第一个关键字65为基准而得到的一趟快速排序结果是（）

A 34，56，25，65，86，99，72，66

B 25，34，56，65，99，86，72，66

C 34，56，25，65，66，99，86，72

D 34，56，25，65，99，86，72，66

题目并未说明使用哪种单趟快排，面对这样的题目，你需要用三种单趟都试试。

2.3递归实现快排

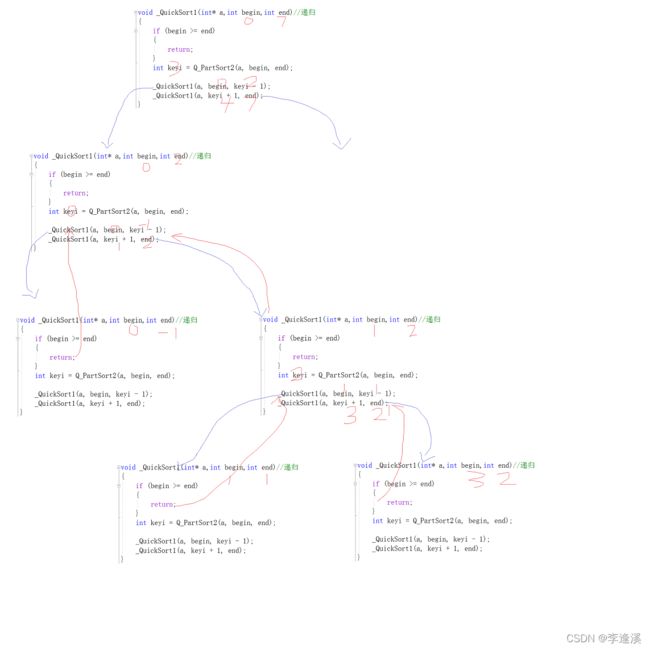
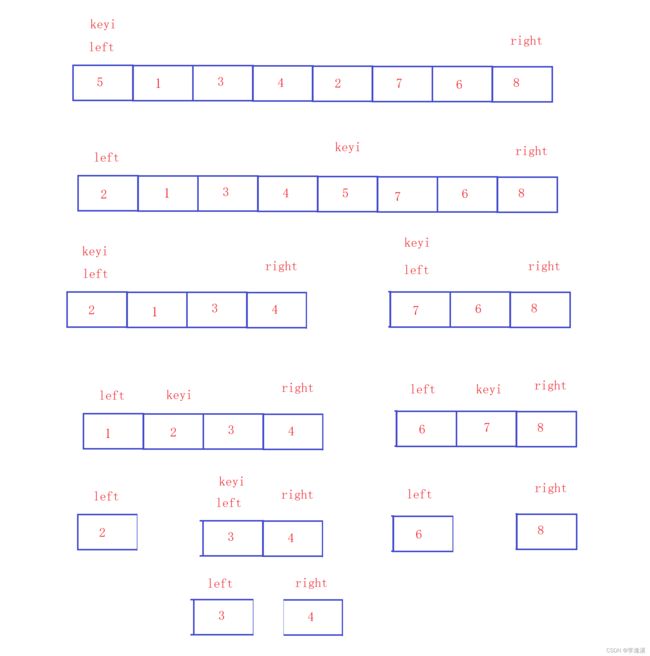
先放参考代码，然后我们再画一画递归的过程。

 参考代码：

void _QuickSort1(int* a,int begin,int end)//递归
{
	if (begin >= end)
	{
		return;
	}
	int keyi = Q_PartSort2(a, begin, end);

	_QuickSort1(a, begin, keyi - 1);
	_QuickSort1(a, keyi + 1, end);
}

 因为空间原因，右半边就不画了。

2.4快排递归算法时间复杂度计算

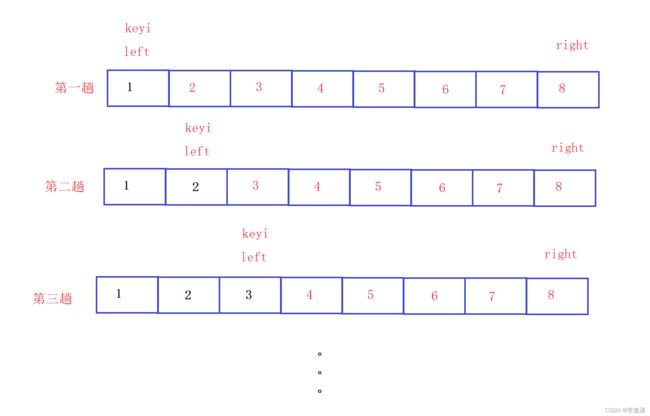
最坏情况：有序

 大概执行次数是T(N) = N+N-1+N-2+.....+3+2+1

时间复杂度是O(N*N)

空间复杂度O（logN）

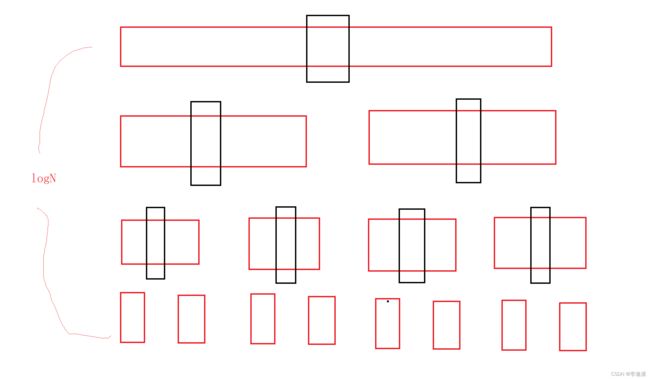
最好情况：每次取的Key都是中位数

相当于一颗满二叉树，高度为 logN

时间复杂度是N*logN

空间复杂度O（logN）

2.5对快排进行优化

2.5.1优化一：三数取中

我们知道有序数组是对快排不利的，从这个角度出发，我们有了三数取中的优化方式：

即选出mid=(left+right)/2

a[left]、a[right]、a[mid]这三个数中，值为中位数的那个数，然后将它于a[keyi]交换。

 参考代码：

int GetMidIndex(int* a, int begin, int end)
{
	int mid = begin + ((end - begin)>>1);
	if (
		(a[mid] >= a[begin] && a[mid] <= a[end])
		|| 
		(a[mid]>=a[end] && a[mid] <= a[begin])
		)
	{
		return mid;
	}
	if (
		(a[begin]<=a[mid] && a[begin]>=a[end])
		||
		(a[begin] >= a[mid] && a[begin] <= a[end])
		)
	{
		return begin;
	}
	return end;
}

int Q_PartSort3(int* a, int begin, int end)//前后指针法
{
	//三数取中优化
	int ki = GetMidIndex(a, begin, end);
	Swap(&a[begin], &a[ki]);
	int keyi = begin;
	int prev = begin;
	int next = begin + 1;
	while (next <= end)
	{
		if (a[next] < a[keyi] && ++prev != next)
		{
			Swap(&a[prev], &a[next]);
		}
		next++;
	}
	Swap(&a[keyi], &a[prev]);
	return prev;
}

2.5.2小区间优化

当区间很小时，直接采用插入排序，就不用继续递归了。

 参考代码：

void _QuickSort1(int* a,int begin,int end)//递归
{
	//小区间优化
	if (end - begin + 1 <= 12)
	{
		InsertSort(a, end - begin + 1);
	}
	if (begin >= end)
	{
		return;
	}
	int keyi = Q_PartSort2(a, begin, end);

	_QuickSort1(a, begin, keyi - 1);
	_QuickSort1(a, keyi + 1, end);
}

最后，一般的排序都是传a和n，为了不传区间，这里加一层封装。

void QuickSort(int* a, int n)
{
	_QuickSort1(a, 0, n - 1);//递归
}

2.6非递归的快排

当要排序的数很多时，可能导致栈溢出，因此需要非递归的快排算法。

这里采用栈+循环来模拟递归调用过程，时间效率上和调用递归并无很大差别。

本质上和调用递归的过程一样

 参考代码：

void _QuickSort2(int* a, int begin, int end)//非递归
{
	ST st;
	STInit(&st);
    //检查传递的end和begin
	if (end > begin)
	{
		STPush(&st, begin);
		STPush(&st, end);
	}
	while (!STEmpty(&st))
	{
		int right = STRear(&st);
		STPop(&st);
		int left = STRear(&st);
		STPop(&st);
		int mid = Q_PartSort2(a, left, right);
        if(left

队列实现快排非递归算法：

 参考代码：

void _QuickSort3(int* a, int begin, int end)//非递归
{
	Queue q;
	QueueInit(&q);
	if (end > begin)
	{
		QueuePush(&q, begin);
		QueuePush(&q, end);
	}
	while (!QueueEmpty(&q))
	{
		int left = QueueFront(&q);
		QueuePop(&q);
		int right = QueueFront(&q);
		QueuePop(&q);
		int keyi = Q_PartSort1(a, left, right);
		if (left < keyi-1)
		{
			QueuePush(&q, left);
			QueuePush(&q, keyi-1);
		}
		if (keyi + 1 < right)
		{
			QueuePush(&q, keyi+1);
			QueuePush(&q, right);
		}
	}
	QueueDestroy(&q);
}