100天精通Python（可视化篇）——第83天：matplotlib绘制不同种类炫酷箱形图参数说明+代码实战（水平、缺口、群组、堆叠、核密度、小提琴箱形图）

专栏导读

本文已收录于《100天精通Python从入门到就业》：本专栏专门针对零基础和需要进阶提升的同学所准备的一套完整教学，从0到100的不断进阶深入，后续还有实战项目，轻松应对面试，专栏订阅地址：https://blog.csdn.net/yuan2019035055/category_11466020.html

• 优点：订阅限时9.9付费专栏进入千人全栈VIP答疑群，作者优先解答机会（代码指导、远程服务），群里大佬众多可以抱团取暖（大厂内推机会）
• 专栏福利：简历指导、招聘内推、每周送实体书、80G全栈学习视频、300本IT电子书：Python、Java、前端、大数据、数据库、算法、爬虫、数据分析、机器学习、面试题库等等
  
  

1. 箱形图介绍

1）箱形图介绍

箱形图（Box-plot）又称为盒须图、盒式图或箱线图，是一种用作显示一组数据分散情况资料的统计图。因形状如箱子而得名。在各种领域也经常被使用，常见于品质管理。它主要用于反映原始数据分布的特征，还可以进行多组数据分布特征的比 较。箱线图的绘制方法是：先找出一组数据的上边缘、下边缘、中位数和两个四分位数；然后， 连接两个四分位数画出箱体；再将上边缘和下边缘与箱体相连接，中位数在箱体中间。箱形图是由首位两个四分位数（Q1，Q3）以及中位数（Q2）组成的，它能够反映出一组数据的基本统计特性，如分布的范围、中位数、变异程度等。

特点：箱形图是概括性较强的一种图，它能够准确反映出数据的主要特点，包括最大值、最小值、四分位数、中位数和实例数，同时观测异常点。

应用场景：箱形图主要用于比较多组数据的分布情况，它非常适用于表示连续变量的分布和比较，是显著进行数据可视化的一种常用工具。

2）怎么看箱型图？

“盒式图"或叫"盒须图”"箱形图"boxplot（也称箱须图(Box-whiskerPlot）须图又称为箱形图，其绘制须使用常用的统计量，能提供有关数据位置和分散情况的关键信息，尤其在比较不同的母体数据时更可表现其差异。

主要包含六个数据节点，将一组数据从大到小排列，分别计算出他的上边缘，上四分位数Q3，中位数，下四分位数Q1，下边缘，还有一个异常值。标示了图中每条线表示的含义，其中应用到了分位值（数）的概念，如下图所示：

3）参数说明

matplotlib绘制箱形图的函数是boxplot()，以下是函数代码：

import matplotlib.pyplot as plt

plt.boxplot(
x, notch=None, sym=None, vert=None, whis=None,
positions=None, widths=None, patch_artist=None,
bootstrap=None, usermedians=None, conf_intervals=None,
meanline=None, showmeans=None, showcaps=None, showbox=None,
showfliers=None, boxprops=None, labels=None, flierprops=None,
medianprops=None, meanprops=None, capprops=None,
whiskerprops=None, manage_ticks=True, autorange=False,
zorder=None, *, data=None)

参数说明如下：

• x：要绘制箱形图的数据，可以是一个数组或多个数组。
• notch：是否绘制缺口箱形图，可选值为True或False，默认为False。
• sym：指定异常值的标记样式，可选值为点（‘.’）、叉号（‘x’）、圆圈（‘o’）等，默认为None。
• vert：指定箱形图的方向，可选值为True（竖向）或False（横向），默认为True。
• patch_artist：是否给箱体填充颜色，可选值为True或False，默认为False。
• meanline：是否绘制均值线，可选值为True或False，默认为False。
• showmeans：是否显示均值，可选值为True或False，默认为False。
• showcaps：是否显示箱线图的上下限制线，可选值为True或False，默认为True。
• showbox：是否显示箱体，可选值为True或False，默认为True。
• showfliers：是否显示异常值，可选值为True或False，默认为True。
• boxprops：指定箱体的属性，如边框颜色、线宽、填充颜色等。
• whiskerprops：指定箱线图的上下限制线的属性，如颜色、线宽等。
• capprops：指定箱线图的上下限制线的帽子的属性，如颜色、线宽等。
• medianprops：指定箱线图的中位数线的属性，如颜色、线宽等。
• meanprops：指定均值线的属性，如颜色、线宽等。
• flierprops：指定异常值的属性，如颜色、大小等。
• manage_xticks：是否自动管理x轴刻度，可选值为True或False，默认为True。
• labels：指定每个数据集的标签。
• notch：是否绘制缺口箱形图，可选值为True或False，默认为False。
• bootstrap：指定计算置信区间时的重抽样次数，默认为10000。

2. 普通箱型图

1）绘图

下面代码绘制一个简单的箱型图，其中Q1、Q3 分别表示上下四分位数；Q2 表示中位数；low_limit、upper_limit 分别表示下限和上限；val 表示异常值。在绘制箱形图时，设置sym="o"即可显示异常值：

import pandas as pd
import matplotlib.pyplot as plt


data = {'num': ['1', '2', '3', '4', '5', '6', '7'],
        'value': [-15, 7, 10, 15, 20, 33, 5]}
df = pd.DataFrame(data)

plt.boxplot(x=df['value'], whis=1.5, widths=0.5, patch_artist=True, showmeans=True, boxprops={'facecolor': 'c'},
            flierprops={'markerfacecolor': 'red', 'markersize': 4},
            meanprops={'marker': '*', 'markerfacecolor': 'skyblue'}, medianprops={'linestyle': '--', 'color': 'orange'},
            capprops={'color': 'r'})

Q1 = df['value'].quantile(q=0.25)
Q2 = df['value'].quantile(q=0.5)
Q3 = df['value'].quantile(q=0.75)

low_limit = Q1 - 1.5 * (Q3 - Q1)
upper_limit = Q3 + 1.5 * (Q3 - Q1)

print('下四分位数:', Q1)
print('中位数:', Q2)
print('上四分位数:', Q3)
print('下限:', low_limit)
print('上限:', upper_limit)

# 查找异常值
val = df['value'][(df['value'] > upper_limit) | (df['value'] < low_limit)]
print('异常值：', val)

#显示图像
plt.show()

运行结果：

2）解释说明

数学层面理解箱形图每个部分的含义(下四分位线，中位数，上四分位数，上限，下限，异常值，极端异常值)：

• 下四分位数：指数据的25%分位点所对应的值（Q1）
• 中位数：指数据的50%分位点所对应的值（Q2）
• 上四分位数：指数据的75%分位点所对应的值（Q3）
• 上限：上限=Q3+1.5*(Q3-Q1)
• 下限：下限=Q1-1.5*(Q3-Q1)
• 异常值的判定标准：当变量的数据值大于上限或小于下限时，判定为异常值

计算方法：

• 1、.数据集：-15, 7, 10, 15, 20, 33, 5
• 2、按从小到大的顺序对数据集进行排列：-15, 5, 7, 10, 15, 20, 33
• 3、确定四分位数索引位置的根据公式：1+(n-1)*数据的百分比分位点，在根据索引位置确定索引所对应的数据值(n是数据集的数量 n=6)
  • Q1_position=1+(6-1)*0.25=2.25 (Q1在第二个数和第三个数之间)
  • Q1_value=15+(36-15)*(2.25-2)=20.25
  • Q2_position=1+(6-1)*0.5=3.5 (Q2在第三个数和第四个数之间)
  • Q2_value=36+(39-36)*(3.5-3)=37.5
  • Q3_position=1+(6-1)*0.75=4.75 (Q3在第四个数和第五个数之间)
  • Q3_value=39+(40-39)*(4.75-4)=39.75
  • 上限=39.75+(39.75-20.25)*1.5=69
  • 下限=20.25-(39.75-20.25)*1.5=-9

极端异常值：

• 极端上限：上限=Q3+3*(Q3-Q1)
• 极端下限：下限=Q1-3*(Q3-Q1)
• 极端异常值的判定标准：当变量的数据值大于极端上限或小于极端下限时，判定为极端异常值

3. 水平箱形图

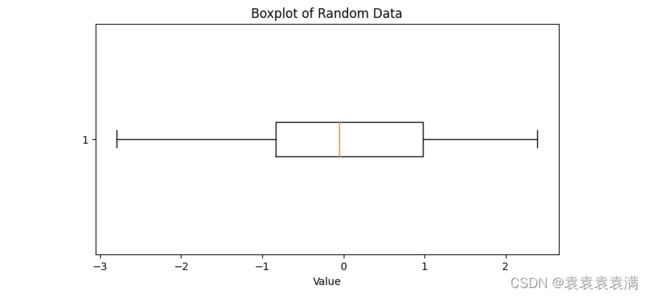
与基本箱形图类似，但是箱形图是水平的，适用于较长的标签或较短的数据集：

import matplotlib.pyplot as plt
import numpy as np

# 生成一组随机数据
np.random.seed(123)
data = np.random.normal(0, 1, 100)

# 绘制水平箱形图
fig, ax = plt.subplots(figsize=(8, 4))
ax.boxplot(data, vert=False)

# 设置图表标题和坐标轴标签
ax.set_title('Boxplot of Random Data')
ax.set_xlabel('Value')

# 显示图表
plt.show()

代码解释：

首先导入matplotlib.pyplot和numpy模块。

使用numpy.random.normal函数生成一组均值为0、标准差为1的正态分布随机数据。

创建一个图表对象fig和一个坐标轴对象ax，并设置图表大小为8x4。

使用坐标轴对象的boxplot方法绘制水平箱形图，其中vert=False表示绘制水平箱形图。

使用坐标轴对象的set_title和set_xlabel方法设置图表标题和坐标轴标签。

使用matplotlib.pyplot的show函数显示图表。

运行结果：

4. 带有缺口的箱形图

在基本箱形图的基础上，为中位数添加一个缺口，以显示置信区间。如果数据中存在离群值（Outlier），箱形图就会失去一些效果。因此，有时候需要绘制带有缺口的箱形图来突出离群值的存在。

在下面示例中，我们使用了 notch=True 参数来绘制缺口。缺口的位置是根据数据分布情况自动计算的。我们还使用了 patch_artist=True 参数来填充箱体的颜色，并使用相应的参数来设置箱体、须、中位数和离群值的样式。最后，我们添加了一些说明来解释图表中的每个部分：

import matplotlib.pyplot as plt
import numpy as np

# 生成随机数据
np.random.seed(10)
data = np.random.normal(100, 20, 200)

# 计算箱形图的五个关键值
q1, median, q3 = np.percentile(data, [25, 50, 75])
iqr = q3 - q1
lower_bound = q1 - 1.5 * iqr
upper_bound = q3 + 1.5 * iqr

# 绘制箱形图
fig, ax = plt.subplots()
ax.boxplot(data, notch=True, vert=False, widths=0.7, patch_artist=True,
           boxprops=dict(facecolor='pink', color='black'),
           whiskerprops=dict(color='black'),
           medianprops=dict(color='black'),
           capprops=dict(color='black'))

# 绘制离群值
outliers = data[(data < lower_bound) | (data > upper_bound)]
ax.scatter(outliers, np.ones(len(outliers)), marker='o', color='black')

# 设置坐标轴
ax.set_yticks([1])
ax.set_yticklabels(['Data'])
ax.set_xlim([80, 120])
ax.axvline(lower_bound, linestyle='--', color='black')
ax.axvline(upper_bound, linestyle='--', color='black')

# 添加说明
ax.text(lower_bound - 2, 1.1, 'Lower\nOutliers', fontsize=10)
ax.text(upper_bound + 2, 1.1, 'Upper\nOutliers', fontsize=10)
ax.text(q1 - 2, 1.2, 'Q1', fontsize=10)
ax.text(median - 2, 1.2, 'Median', fontsize=10)
ax.text(q3 - 2, 1.2, 'Q3', fontsize=10)

plt.show()

运行结果：

5. 群组箱形图

群组箱形图（Grouped box plot）是一种用于比较多组数据分布情况的图表。它用于比较两个或多个数据集的中位数、四分位数和异常值。可以将多组数据按照分类变量分组，并在同一图表中展示出来，以便于比较不同组之间的差异。

在下面示例中，我们使用了 labels 参数将数据按照分类变量分组，并使用了 vert=False 参数将图表方向设置为水平方向。我们还使用了相应的参数来设置箱体、须、中位数的样式，并使用了 patch_artist=True 参数来填充箱体的颜色。最后，我们添加了标题和标签来解释图表的含义：

import matplotlib.pyplot as plt
import numpy as np

# 生成随机数据
np.random.seed(10)
data1 = np.random.normal(100, 20, 200)
data2 = np.random.normal(80, 15, 200)
data3 = np.random.normal(120, 25, 200)
data4 = np.random.normal(90, 10, 200)

# 将数据按照分类变量分组
data = [data1, data2, data3, data4]
labels = ['Group 1', 'Group 2', 'Group 3', 'Group 4']

# 绘制群组箱形图
fig, ax = plt.subplots()
ax.boxplot(data, labels=labels, vert=False, patch_artist=True,
           boxprops=dict(facecolor='pink', color='black'),
           whiskerprops=dict(color='black'),
           medianprops=dict(color='black'),
           capprops=dict(color='black'))

# 设置坐标轴
ax.set_xlim([50, 150])

# 添加标题和标签
ax.set_title('Grouped Box Plot')
ax.set_xlabel('Value')
ax.set_ylabel('Group')

plt.show()

运行结果：

6. 堆叠箱形图

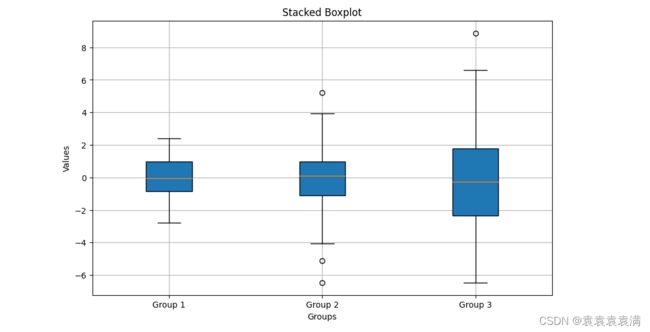
堆叠箱形图（Stacked box plot）是一种用于比较两个或多个数据集的分布情况，将箱形图堆叠在一起。它可以将多组数据按照分类变量分组，并在同一图表中展示出来，并且在每个组内部又按照另一个分类变量进行分层，以便于比较不同组之间和不同层之间的差异。

堆叠箱形图显示了三个组之间的分布，每个组有100个观测值。每个箱子代表每个组的中位数、上下四分位数和最大/最小值。箱子的颜色表示每个组的标识符，即Group 1、Group 2和Group 3。可以看到，Group 1和Group 3的数据分布相似，而Group 2的数据分布略有不同：

import matplotlib.pyplot as plt
import numpy as np

# 生成数据集
np.random.seed(123)
data = [np.random.normal(0, std, 100) for std in range(1, 4)]


# 绘制堆叠箱形图
fig, ax = plt.subplots(figsize=(10, 6))
ax.boxplot(data, vert=True, patch_artist=True, labels=['Group 1', 'Group 2', 'Group 3'])

# 显示网格
plt.grid(True)  

# 设置箱子颜色
colors = ['#0000FF', '#FFA500', '#00FFFF']
for patch, color in zip(ax.artists, colors):
    patch.set_facecolor(color)

# 添加标题和标签
ax.set_title('Stacked Boxplot')
ax.set_xlabel('Groups')
ax.set_ylabel('Values')

# 展示图表
plt.show()

运行结果：

7. 核密度估计箱形图

核密度估计箱形图是一种结合了核密度估计和箱形图的图表，添加核密度估计曲线，它可以更准确地反映数据的分布情况，并且能够同时显示出异常值等信息：

import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns

# 生成一组随机数据
np.random.seed(123)
data = np.random.normal(0, 1, 100)

# 绘制核密度估计箱形图
fig, ax = plt.subplots(figsize=(8, 4))
sns.boxplot(x=data, ax=ax, color='lightblue')
sns.kdeplot(x=data, ax=ax, color='blue', linewidth=2)

# 设置图表标题和坐标轴标签
ax.set_title('Kernel Density Estimation Boxplot of Random Data')
ax.set_xlabel('Value')

# 显示图表
plt.show()

代码解释：

首先导入matplotlib.pyplot、numpy和seaborn模块。

使用numpy.random.normal函数生成一组均值为0、标准差为1的正态分布随机数据。

创建一个图表对象fig和一个坐标轴对象ax，并设置图表大小为8x4。

使用seaborn的boxplot方法绘制箱形图，并设置颜色为'lightblue'。

使用seaborn的kdeplot方法绘制核密度估计图，并设置颜色为'blue'、线宽为2。

使用坐标轴对象的set_title和set_xlabel方法设置图表标题和坐标轴标签。

使用matplotlib.pyplot的show函数显示图表。

运行结果：

8. 小提琴箱形图

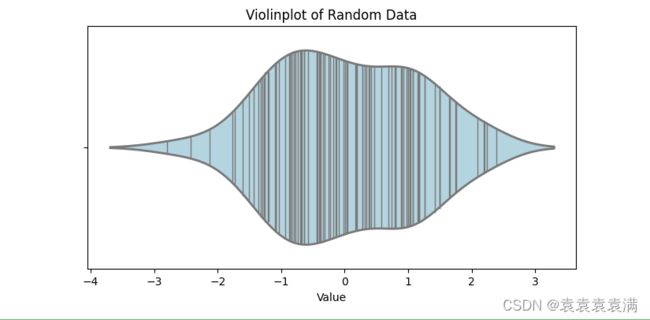
小提琴箱形图是一种结合了箱形图和核密度估计的图表，它可以更好地反映数据的分布情况，并且能够同时显示出异常值等信息：

import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns

# 生成一组随机数据
np.random.seed(123)
data = np.random.normal(0, 1, 100)

# 绘制小提琴箱形图
fig, ax = plt.subplots(figsize=(8, 4))
sns.violinplot(x=data, ax=ax, color='lightblue', inner='stick', linewidth=2)

# 设置图表标题和坐标轴标签
ax.set_title('Violinplot of Random Data')
ax.set_xlabel('Value')

# 显示图表
plt.show()

代码解释：

首先导入matplotlib.pyplot、numpy和seaborn模块。

使用numpy.random.normal函数生成一组均值为0、标准差为1的正态分布随机数据。

创建一个图表对象fig和一个坐标轴对象ax，并设置图表大小为8x4。

使用seaborn的violinplot方法绘制小提琴箱形图，并设置颜色为'lightblue'、内部样式为'stick'、线宽为2。

使用坐标轴对象的set_title和set_xlabel方法设置图表标题和坐标轴标签。

使用matplotlib.pyplot的show函数显示图表。

运行结果：