算法自学__单调队列

参考资料：

• https://zhuanlan.zhihu.com/p/346354943

算法简介

单调队列可以在 $O(n)$ 的时间复杂度内，求出长度为 $n$ 的序列中，每个长度为 $m$ 的区间的最值。

算法思想

形象地理解：每轮循环中，先检查队头的“学长”是否毕业，再队列中比“新生”菜的学长全部踢出，最后让新生入队。

具体的算法思想见参考资料。

例1 P2216 [HAOI2007]理想的正方形

题目描述

有一个 $a\times b$ 的整数组成的矩阵，现请你从中找出一个 $n\times n$ 的正方形区域，使得该区域所有数中的最大值和最小值的差最小。

输入格式

第一行为 $3$ 个整数，分别表示 $a,b,n$ 的值。

第二行至第 $a+1$ 行每行为 $b$ 个非负整数，表示矩阵中相应位置上的数。每行相邻两数之间用一空格分隔。

输出格式

仅一个整数，为 $a\times b$ 矩阵中所有 $n\times n$ 正方形区域中的最大整数和最小整数的差值”的最小值。

样例 #1

样例输入 #1

5 4 2
1 2 5 6
0 17 16 0
16 17 2 1
2 10 2 1
1 2 2 2

样例输出 #1

1

提示

矩阵中的所有数都不超过 $1,000,000,000$。

$100\%$ 的数据 $2\le a,b\le 1000,n\le a,n\le b,n\le 100$。

思路

总体思路：用单调队列求出每个 $n\times n$ 的正方形的中最大值和最小值，然后遍历每个正方形，更新答案。

以求正方形内的最大值为例。先扫描输入矩阵每一行，求出每一行的每一个长度为 $n$ 的区间的最大值，保存在矩阵 mmax[][] 中。然后扫描 mmax[][] 中合法的每一列，求出每一列的每一个长度 $n$ 的区间的最大值，保存在矩阵 mmmax[][] 中。

代码

#include
using namespace std;

const int maxn = 1e3+5;

int a, b, n;
int mtx[maxn][maxn];
int mmax[maxn][maxn];
int mmmax[maxn][maxn];
int mmin[maxn][maxn];
int mmmin[maxn][maxn];
int ans = 0x7fffffff; 

int main(){
	ios::sync_with_stdio(false);
	cin.tie(0); cout.tie(0);
	cin>>a>>b>>n;
	for(int i=1;i<=a;i++){
		for(int j=1;j<=b;j++){
			cin>>mtx[i][j];
		}
	}
	// 求正方形内最大值
	for(int i=1;i<=a;i++){
		deque<int> q;
		for(int j=1;j<=b;j++){
			if(!q.empty() && j-q.front()+1>n) q.pop_front();
			while(!q.empty() && mtx[i][j]>mtx[i][q.back()]) q.pop_back();
			q.push_back(j);
			if(j>=n){
				mmax[i][j] = mtx[i][q.front()];
			}
		}
	} 
	for(int j=n;j<=b;j++){
		deque<int> q;
		for(int i=1;i<=a;i++){
			if(!q.empty() && i-q.front()+1>n) q.pop_front();
			while(!q.empty() && mmax[i][j]>mmax[q.back()][j]) q.pop_back();
			q.push_back(i);
			if(i>=n){
				mmmax[i][j] = mmax[q.front()][j];
			}
		}
	}
	// 求正方形内最小值 
	for(int i=1;i<=a;i++){
		deque<int> q;
		for(int j=1;j<=b;j++){
			if(!q.empty() && j-q.front()+1>n) q.pop_front();
			while(!q.empty() && mtx[i][j]<mtx[i][q.back()]) q.pop_back();
			q.push_back(j);
			if(j>=n){
				mmin[i][j] = mtx[i][q.front()];
			}
		}
	} 
	for(int j=n;j<=b;j++){
		deque<int> q;
		for(int i=1;i<=a;i++){
			if(!q.empty() && i-q.front()+1>n) q.pop_front();
			while(!q.empty() && mmin[i][j]<mmin[q.back()][j]) q.pop_back();
			q.push_back(i);
			if(i>=n){
				mmmin[i][j] = mmin[q.front()][j];
			}
		}
	}
	// 求最终答案 
	for(int i=n;i<=a;i++){
		for(int j=n;j<=b;j++){
			ans = min(ans, mmmax[i][j]-mmmin[i][j]);
		}
	}
	cout<<ans; 
	return 0;
}

例2 P2034 选择数字

题目描述

给定一行 $n$ 个非负整数 $a_1\cdots a_n$。现在你可以选择其中若干个数，但不能有超过 $k$ 个连续的数字被选择。你的任务是使得选出的数字的和最大。

输入格式

第一行两个整数 $n$，$k$。

以下 $n$ 行，每行一个整数表示 $a_i$。

输出格式

输出一个值表示答案。

样例 #1

样例输入 #1

5 2
1
2
3
4
5

样例输出 #1

12

提示

对于 $100\%$ 的数据，$1\le n\le 100000$，$1\le k\le n$，$0\le$ 数字大小 $\le 1,000,000,000$。

思路

本题是单调队列优化动态规划的经典例题。

将题目转化为：从题目中删除若干数字，且任意两个被删除的数字的序号的差小于等于 k 。在满足题目要求的前提下，要使被删除数字的和尽可能地小。

定义状态 dp[i] 表示： 仅考虑前 i 个数字，且删除第 i 个数字的情况下，被删除的最小和。状态转移方程为：
$$dp[i]=\{\begin{array}{l}a[i],i\le k+1\\ a[i]+\underset{i-k-1\le j\le i-1}{\min }dp[j],i>k+1\end{array}$$

可以看出，状态转移需要使用定长区间的最值，故可以使用单调队列优化。

代码

#include
#define int long long
using namespace std;

const int maxn = 1e5+5; 

int n, k;
int a[maxn];
int dp[maxn];
int sum = 0;
int ans = 0x7fffffff;
deque<int> q;

signed main(){
	cin>>n>>k;
	k += 1;
	for(int i=1;i<=n;i++){
		cin>>a[i];
		sum += a[i];
	}
	for(int i=1;i<=n;i++){
		if(!q.empty() && i>k) dp[i] += dp[q.front()];
		dp[i] += a[i];
		if(!q.empty() && i-q.front()+1>k) q.pop_front();
		while(!q.empty() && dp[i]<dp[q.back()]) q.pop_back();
		q.push_back(i);
	}
	ans = sum;
	for(int i=n-k+1;i<=n;i++){
		ans = min(ans, dp[i]);
	}
	cout<<sum-ans;
	return 0;
}

例3 P2698 [USACO12MAR]Flowerpot S

题目描述

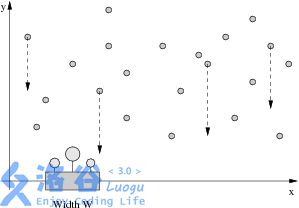
老板需要你帮忙浇花。给出 $N$ 滴水的坐标，$y$ 表示水滴的高度，$x$ 表示它下落到 $x$ 轴的位置。

每滴水以每秒 $1$ 个单位长度的速度下落。你需要把花盆放在 $x$ 轴上的某个位置，使得从被花盆接着的第 $1$ 滴水开始，到被花盆接着的最后 $1$ 滴水结束，之间的时间差至少为 $D$。

我们认为，只要水滴落到 $x$ 轴上，与花盆的边沿对齐，就认为被接住。给出 $N$ 滴水的坐标和 $D$ 的大小，请算出最小的花盆的宽度 $W$。

输入格式

第一行 $2$ 个整数 $N$ 和 $D$。

接下来 $N$ 行每行 $2$ 个整数，表示水滴的坐标 $(x,y)$。

输出格式

仅一行 $1$ 个整数，表示最小的花盆的宽度。如果无法构造出足够宽的花盆，使得在 $D$ 单位的时间接住满足要求的水滴，则输出 $-1$。

样例 #1

样例输入 #1

4 5
6 3
2 4
4 10
12 15

样例输出 #1

2

提示

$100\%$ 的数据：$1\le N\le 10^5$ ，$1\le D\le 10^6$ ，$0\le x,y\le 10^6$ 。

思路

二分答案+单调队列

需要注意的是，队头出队的条件是：当前水滴与队头水滴的 $x$ 坐标之差大于花盆宽度。

代码

#include
using namespace std;

const int maxn = 1e5+5;

struct NODE{
	int x, y;
	bool operator<(const NODE& a)const{
		if(x==a.x) return y<a.y;
		else return x<a.x;
	}
};

NODE node[maxn];
int n, d;
int m = 0x7fffffff, M = -1;
int L = 0x7fffffff, R = -1;
int ans = 0x7fffffff;

bool check(int len){
	deque<int> q1, q2;
	for(int i=1;i<=n;i++){
		if(!q1.empty() && node[i].x-node[q1.front()].x>len) q1.pop_front();
		if(!q2.empty() && node[i].x-node[q2.front()].x>len) q2.pop_front();
		while(!q1.empty() && node[i].y>node[q1.back()].y) q1.pop_back();
		while(!q2.empty() && node[i].y<node[q2.back()].y) q2.pop_back();
		q1.push_back(i);
		q2.push_back(i);
		if(node[q1.front()].y-node[q2.front()].y >= d) return true;
	}
	return false;
}

int main(){
	ios::sync_with_stdio(false);
	cin.tie(0); cout.tie(0);
	cin>>n>>d;
	for(int i=1;i<=n;i++){
		cin>>node[i].x>>node[i].y;
		m = min(m, node[i].y);
		M = max(M, node[i].y);
		L = min(L, node[i].x);
		R = max(R, node[i].x);
	} 
	sort(node+1, node+1+n);
	R = R-L, L = 0;
	if(M-m<d){
		cout<<-1;
		return 0;
	}
	while(L <= R){
		int mid = (L+R)>>1;
		if(check(mid)){
			ans = min(ans, mid);
			R = mid-1;
		}
		else{
			L = mid+1;
		}
	}
	cout<<ans;
	return 0;
}