Python数据结构与算法之二叉树的遍历

二叉树的遍历

      树的遍是树的一种重要的运算。所谓遍历是指对树中所有节点的信息访问，即一次对树中每个节点当问一次且仅访问一次，我们把这种对所有节点的访问称为遍历（travelsal）。
      树的两种重要的遍历模式是深度优先遍历和广度优先遍历，深度优先一般用递归，广度优先一般用队列。一般情况下能用递归实现的算法大部分也能用堆栈来实现。

深度优先遍历

      对于一棵二叉树，深度优先搜索（Depth First Search）是沿着树的深度遍历树的节点，尽可能深得搜索树的分支。
      深度遍历有三种方法。这三种常用于访问树的节点，它们之间的不同在于访问每个节点的次序不同。这三种遍历分别叫做先序遍历（preorder），中序遍历（inorder）和后序遍历（postorder）。

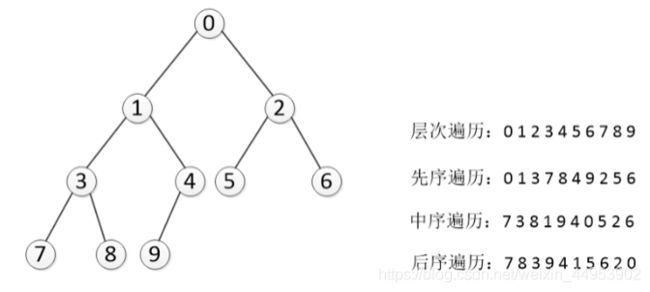
• 先序遍历：在先序遍历中，先访问根节点，然后递归使用先序遍历访问左子树，再递归使用先序遍历访问右子树。根节点–>左子树–>右子树

def preorder(self,node):
    if node is None:
        return
    print(node.elem,end=" ")
    self.preorder(node.lchild)
    self.preorder(node.rchild)

• 中序遍历：在中序遍历中，先递归使用中序遍历访问左子树，然后访问根节点，最后递归使用终须遍历访问右子树。左子树–>根节点–>右子树

def inorder(self,node):
    if node is None:
        return
    self.inorder(node.lchild)
    print(node.elem,end=" ")
    self.inorder(node.rchild)

• 后序遍历：在后序遍历中，先递归使用后序遍历访问左子树和右子树，最后访问根节点。左子树–>右子树–>根节点

def postorder(self,node):
    if node is None:
        return
    self.postorder(node.lchild)
    self.postorder(node.rchild)
    print(node.elem,end=" ")

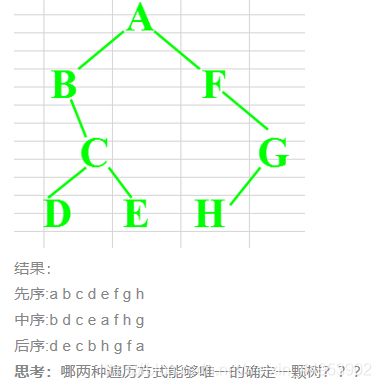
      使用中序和先序或者后序中的任何一个便可以到位唯一确定的一棵树。

广度优先遍历（层次遍历）

      从树的root开始，从上到下从左到右遍历整个树的节点

def breadth_travel(self):
    """广度遍历"""
    queue = [self.root]
    if self.root is None:
        return
    while queue:
        cur_node = queue.pop(0)
        print(cur_node.elem,end=" ")
        if cur_node.lchild is not None:
            queue.append(cur_node.lchild)
        if cur_node.rchild is not None:
            queue.append(cur_node.rchild)

测试：

if __name__ == "__main__":
    tree = Tree()
    tree.add(0)
    tree.add(1)
    tree.add(2)
    tree.add(3)
    tree.add(4)
    tree.add(5)
    tree.add(6)
    tree.add(7)
    tree.add(8)
    tree.add(9)
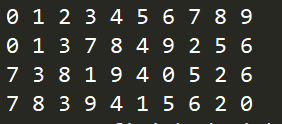
    tree.breadth_travel()
    print(" ")
    tree.preorder(tree.root)
    print(" ")
    tree.inorder(tree.root)
    print(" ")
    tree.postorder(tree.root)

结果：