线段树入门——AtCoder Beginner Contest 285（F - Substring of Sorted String）讲解

蒟蒻来讲题，还望大家喜。若哪有问题，大家尽可提！

Hello, 大家好哇！本初中生蒟蒻今天以AtCoder Beginner Contest 285的F题——Substring of Sorted String为例，给大家讲解一下线段树入门基础！

===========================================================================================

线段树入门

线段树的概念

线段树是一种二叉搜索树，与区间树相似，它将一个区间划分成一些单元区间，每个单元区间对应线段树中的一个叶结点。使用线段树可以快速的查找某一个节点在若干条线段中出现的次数，时间复杂度为O(logN)。而未优化的空间复杂度为2N，实际应用时一般还要开4N的数组以免越界，因此有时需要离散化让空间压缩。

线段树的操作

Pushup（Pushdown后面再讲）

pushup操作就是从叶结点不断向上回溯，同时不断更新父节点的值。

模板

inline void pushup(int u)
{
		//求最大值
    tree[u].v = max(tree[u << 1].v, tree[u << 1 | 1].v);
    //求最小值
    tree[u].v = min(tree[u << 1].v, tree[u << 1 | 1].v);
    //求和
    tree[u].v = tree[u << 1].v + tree[u << 1 | 1].v;
}

建树（build操作）

建树即为从根节点不断的向下递归，分出每一个节点（除了叶结点）的左子树和右子树，并进行赋值回溯。

模板

inline void build(int u, int l, int r)
{
    tree[u].l = l, tree[u].r = r;//更新左端点，右端点
    
    if (l == r) return; //叶结点，回溯
    
    int mid = l + r >> 1; 中间点——分出左子树和右子树
    build(u << 1, l, mid); //建立左子树
    build(u << 1 | 1, mid + 1, r); //建立右子树
		pushup(u);
}

修改单点（modify操作）

修改单点就是不断向下找到叶结点进行更改，在进行一次Pushup操作，更新父节点

模板

inline void modify(int u, int x, int c) //将点x改成c
{
    if (tree[u].l == x && tree[u].r == x) tree[u].v = c; //枚举到叶结点
    else 
    {
        int mid = tree[u].l + tree[u].r >> 1;
        if (x <= mid) modify(u << 1, x, c); //说明x在左子树中
        else modify(u << 1 | 1, x, c);//说明x在右子树中

        pushup(u);//向上更新父节点
    }

    return;
}

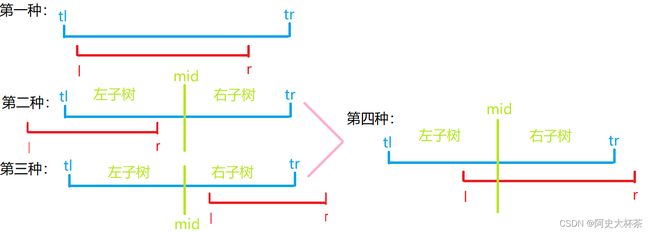
查询区间（query操作）

查询区间分三种情况：

• 树节点的区间被查询的区间完全包含，那么直接返回该节点的值
• 查询区间的左端点在mid的左边，说明在左子树
• 查询区间的右端点在mid的右边，说明在右子树
• 第四种其实就是2,3种的结合，所以2,3中的判断条件都得是if，而不能是else if或else

模板

inline int query(int u, int l, int r)
{
    if (tree[u].l >= l && tree[u].r <= r) return tree[u].v; //第一种

    int mid = tree[u].l + tree[u].r >> 1, v = 0;
    if (l <= mid) v = query(u << 1, l, r); //第二种
    if (r > mid) v = max(v, query(u << 1 | 1, l, r)); //第三种
    return v;
}

到此为止，线段树入门的函数就讲完了，下面我们来举个例子，说明如何应用。

实例讲解（F - Substring of Sorted String）

原题

Problem Statement

You are given a string $S$ of length $N$ consisting of lowercase English letters, and $Q$ queries. Process the queries in order.

Each query is of one of the following two kinds:

• $1$ $x$ $c$ : replace the $x$-th character of S by the character $c$.
• $2$ $l$ $r$ : let $T$ be the string obtained by sorting the characters of $S$ in ascending order. Print $Yes$ if the string consisting of the $l$-th through $r$-th characters of $S$ is a substring of $T$; print $No$ otherwise.

Constraints

• $1\le N\le 10^5$
• $S$ is a string of length
• $N$ consisting of lowercase English letters.
• $1\le Q\le 10^5$
• For each query of the first kind, $1\le x\le N$.
• For each query of the first kind, $c$ is a lowercase English letter.
• For each query of the second kind, $1\le l\le r\le N$.

Input

The input is given from Standard Input in the following format, where
query $i$ denotes the $i$-th query:

N  S  Q
query1​
query2​
⋮
queryQ​

Output

Process the queries as instructed in the Problem Statement.

Sample Input 1

6
abcdcf
4
2 1 3
2 2 6
1 5 e
2 2 6

Sample Output 1

Yes
No
Yes

• In the $1$-st query, abccdf is the string $T$ obtained by sorting the characters of S in ascending order. The string abc, consisting of the $1$-st through $3$-rd characters of $S$, is a substring of $T$, so Yes should be printed.
• In the $2$-nd query, abccdf is the string $T$ obtained by sorting the characters of S in ascending order. The string bcdcf, consisting of the $2$-nd through $6$-th characters of $S$, is not a substring of $T$, so No should be printed.
• The $3$-rd query sets the 5-th character of S to e, making $S$ $abcdef$.
• In the $4$-th query, abcdef is the string $T$ obtained by sorting the characters of S in ascending order. The string $bcdef$, consisting of the $2$-nd through $6$-th characters of $S$, is a substring of $T$, so $Yes$ should be printed.

---

思路

本题中若想要将两个区间匹配的话，必须满足以下2个条件：

• 区间内的字母必须是升序
• 区间内的每个字母（除了左端点和右端点）在区间中出现的个数，必须和在整个字符串中出现的次数相同。

故能得出以下代码：（带详细注释）

---

代码

#include 
#include 

using namespace std;

const int N = 1e6 + 10, M = 3e1 + 10;

int n, q;
int all[M], section[M]; //整体和区间的字母个数
string s;
struct node
{
	int l, r; //注意l, r存的是字母，不是下标
	int cnt[M];//记录该树中每个字母出现的个数
	bool st; //判断是否满足升序条件
}tree[4 * N];

inline void pushup(int u) //由下到上回溯
{
	for (int i = 1; i <= 26; i ++)
		tree[u].cnt[i] = tree[u << 1].cnt[i] + tree[u << 1 | 1].cnt[i]; //父节点字母个数 = 左结点字母个数 + 左结点字母个数
	
	tree[u].st = (tree[u << 1].st & tree[u << 1 | 1].st) & (tree[u << 1].r <= tree[u << 1 | 1].l); //判断是否有节点并且按升序排列
	tree[u].l = tree[u << 1].l, tree[u].r = tree[u << 1 | 1].r; //更新父节点的左右端点
}

inline void build(int u, int tl, int tr) //建树
{
	if (tl == tr) //是一棵叶结点
	{
		tree[u].l = tree[u].r = (s[tl] - 'a' + 1); //左端点，右端点记录为当前字符
		tree[u].cnt[s[tl] - 'a' + 1] ++; //在这棵子树中该字母出现的次数+1
		tree[u].st = 1; //标记当前有一棵树
		return;
	}
	
	int mid = tl + tr >> 1; //中间点——分出左子树和右子树
	build(u << 1, tl, mid);//建立左子树
	build(u << 1 | 1, mid + 1, tr);//建立右子树
	
	pushup(u);//从下向上更新父节点
}

inline void modify(int u, int tl, int tr, int x, char c)
{
	if (tl == tr) //是叶结点
	{
		int hashi = s[x] - 'a' + 1;
		tree[u].cnt[hashi] --; //将当前字符在本棵树中的次数减1
		all[hashi] --; //将当前字符在整个字符串中的次数减1
		//---------------------删除该字母操作---------------------
		hashi = c - 'a' + 1;
		tree[u].cnt[hashi] ++;//将更改后的字符在本棵树中的次数加1
		all[hashi] ++;//将更改后字符在整个字符串中的次数加1
		s[x] = c;
		//---------------------添加该字母操作---------------------
		tree[u].l = tree[u].r = hashi; //更新左端点，右端点
		return;
	}
	
	int mid = tl + tr >> 1;
	if (x <= mid) modify(u << 1, tl, mid, x, c); //说明x在左子树中
	else modify(u << 1 | 1, mid + 1, tr, x, c); //说明x在右子树中
	pushup(u); //由于更新了值，所以要“顺藤摸瓜”地更新父节点
}

inline bool query(int u, int tl, int tr, int l, int r) //查询（是否满足升序条件）
{
	if (tl >= l && tr <= r) //查询的区间包含该节点表示的区间
	{
		for (int i = 1; i <= 26; i ++) section[i] += tree[u].cnt[i]; //记录区间内每个字母出现的次数
		return tree[u].st; //确定是否是一棵节点并且是否满足升序条件
	}
	
	int mid = tl + tr >> 1;
	int left = 1;
	bool flg = 1;
	if (l <= mid)
		flg &= query(u << 1, tl, mid, l, r), left = tree[u << 1].r; 
	if (r > mid)
		flg &= query(u << 1 | 1, mid + 1, tr, l, r) & (left <= tree[u << 1 | 1].l); //若左子树的右边的字母小于右子树的左边的字母，即能判断出升序
	
	return flg;
}

inline bool judge(int l, int r) //判断字母个数相同以及升序
{
	memset(section, 0, sizeof section); //首先每次清空
	
	if (!query(1, 1, n, l, r)) return 0; //若不是升序，不行
	
	int mn = 27, mx = 0; //计算区间最大字母和最小字母
	for (int i = 1; i <= 26; i ++) 
		if (section[i])
			mn = min(mn, i), mx = max(mx, i);
			
	for (int i = mn + 1; i < mx; i ++)
		if (section[i] < all[i])
			return 0; //如果数量不匹配，返回0
			
	return 1;
}

int main()
{
	cin.tie(0);
	ios::sync_with_stdio(0);
	
	cin >> n >> s >> q;
//-------读入--------

	s = ' ' + s; //让s下标从1开始	
	for (int i = 1; i <= n; i ++)
		all[s[i] - 'a' + 1] ++;
		
//-------计算每个字符出现的次数-----------
		
	build(1, 1, n);
//-------建树--------
	
	while (q --)
	{
		int op, t1;
		cin >> op >> t1;
				
//--------读入询问-------------
		
		if (op == 1) //更改操作
		{
			char t2;
			
			cin >> t2;
			
			modify(1, 1, n, t1, t2);
		}
		else //查询操作
		{
			int t2;
			cin >> t2;
			
			bool res = judge(t1, t2);
			
			(res) ? puts("Yes") : puts("No");
		}
	}
	
	return 0;
}

---

今天就到这里了！

大家有什么问题尽管提，我都会尽力回答的！最后，大年初二祝大家新年快乐！

吾欲您伸手，点的小赞赞。吾欲您喜欢，点得小关注！