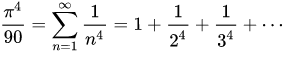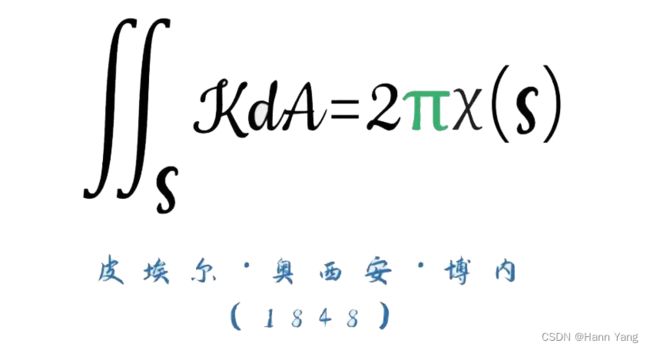今天是国际数学日，既是爱因斯坦的生日又是霍金的忌日

目录

一、库函数计算 π

二、近似值计算 π

三、无穷级数计算 π

四、割圆术计算 π

五、蒙特卡罗法计算 π

六、计算800位精确值

---

从2020年开始，每年的3月14日又被定​为国际数学日​，是2019年11月26日​联合国教科文组织​第四十届大会上正式宣布的。巧合的是这一天既是爱因斯坦的生日，又是霍金的忌日，两位物理界的巨擘一个出生于(1879)另一个离世于(2018)这个日子。

以前，3月14日还是一年一度的庆祝常数π的节日，由圆周率最常用的近似值3.14而来，称为圆周率日（π Day）。

圆周率（π）是圆的周长与直径的比值，一般用希腊字母π表示，是一个在数学及物理学中普遍存在的数学常数。π也等于圆形之面积与半径平方之比，是精确计算圆周长、圆面积、球体积等几何形状的关键值。

公元263年，中国数学家刘徽用“割圆术”计算圆周率，他先从圆内接正六边形，逐次分割一直算到圆内接正192边形，给出π=3.141024的圆周率近似值。他说：“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣。”这包含了求极限的思想。

公元480年左右，南北朝时期的数学家祖冲之进一步得出精确到小数点后7位的结果，给出不足近似值3.1415926和过剩近似值3.1415927，还得到两个近似分数值，密率355/113和约率22/7。密率是个很好的分数近似值，要取到才能得出比略准确的近似。在之后的800年里祖冲之计算出的π值都是最准确的。

计算机的出现使π值计算有了突飞猛进的发展。经吉尼斯世界纪录认证，目前π的最准确值，超过小数点后62,831,853,071,796位。

---

今天来用python代码来算算圆周率 π，也算比较应景的。方法有很多，列举几个如下：

一、库函数计算 π

>>> import math
>>> math.pi
3.141592653589793
>>> math.acos(-1)
3.141592653589793
>>> math.atan(1)*4
3.141592653589793
>>> math.atan2(2,2)*2*2
3.141592653589793

二、近似值计算 π

>>> print(22/7)
3.142857142857143
>>> print(355/113)
3.1415929203539825
>>> print(102573/32650)
3.141592649310873
>>> import math
>>> print(16*math.atan(1/5)-4*math.atan(1/239))
3.1415926535897936
>>> print(32*math.atan(1/10)-4*math.atan(1758719/147153121))
3.1415926535897936
>>> math.pi #比对
3.141592653589793

三、无穷级数计算 π

π/4 = 1 - 1/3 + 1/5 - 1/7 + 1/9 - 1/11 + 1/13 - 1/15 ...

pi=0
for i in range(1,10000000):
    pi+=0.5/(i**2-i+0.1875)

print(pi)

'''
3.1415926035880934
>>> 
'''

π = 3 + 4/(2*3*4) - 4/(4*5*6) + 4/(6*7*8) - 4/(8*9*10) + 4/(10*11*12) - 4/(12*13*14) ...

pi=3
for i in range(2,10000000,4):
    pi+=4/(i*(i+1)*(i+2))-4/((i+2)*(i+3)*(i+4))

print(pi)

'''
3.1415926535895253
>>> 
'''

from math import  sqrt
pi=0
for i in range(1,10000000,2):
    pi+=1/(i*i)

print(sqrt(8*pi))

'''
3.141592589927253
>>> 
'''

from math import  sqrt
pi=0
for i in range(1,10000000):
    pi+=1/(i**4)

print(sqrt(sqrt(90*pi)))

'''
3.141592653589592
>>> 
'''

印度天才数学家拉马努金1914年发表了一个圆周率计算公式，每计算一项可以得到8位的十进制精度；以上公式由Jonathan Borwein和Peter Borwein兄弟俩在1987年用基于椭圆积分变换的理论给出证明并改良过后的公式。

from math import  sqrt
from math import  factorial

for j in range(1,6):
    pi=0
    for i in range(j):
        pi+= (26390*i+1103)*factorial(4*i)/(factorial(i)**4)/(396**(4*i))
    print("%.20f"%(1/(2*sqrt(2)*pi/9801)))


'''
3.14159273001330552333
3.14159265358979400418
3.14159265358979311600
3.14159265358979311600
3.14159265358979311600
>>> 
'''

以上代码算到第三项就到精度极限了，应该是python本身精度不够引起的。

四、割圆术计算 π

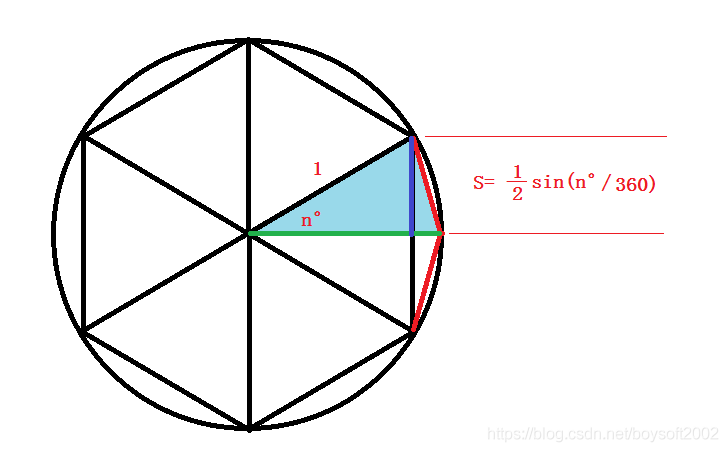
割圆术：古代(魏晋)数学家刘徽 公元263年《九章算术注》记载，现代数学用三角函数来表示分割的三角形面积，如下切割3亿份就能得到15位精度

>>> from math import sin
>>> sin(2*math.pi/300000000)*300000000/2
3.141592653589793

五、蒙特卡罗法计算 π

方法：单位圆外接一个正方形，然后向其中随机撒点，通过计算落在圆内的点数与总点数之比计算圆周率。以圆心为原点坐标，计算点与原点的距离，距离不于1的有效点数 hits 增一。

from random import random

Dots = 2000000

for j in range(5):
    hits = 0
    for i in range(Dots):
        x,y = random(),random()
        dist = (x**2+y**2)**0.5
        if dist <= 1.0:
            hits+=1
    pi = 4 * (hits/Dots)
    print(pi)

 每次计算距离有三次 ** 运算，所以速度有点慢；精度也不高，200万个点能得出 3.14 两位精度。

六、计算800位精确值

a,c=10000,2800
b=e=0
f=[0]*2801
while b!=c:
    f[b]=a//5
    b+=1
while c!=0:
    d=0
    g=c*2
    b=c
    while 1:
        d+=f[b]*a
        g-=1
        f[b]=d%g
        d//=g
        g-=1
        b-=1
        if b!=0:
            d*=b
        else:
            break
    c-=14
    print('%.4d'%(e+d//a),end='')
    e=d%a

 这段代码比较神奇的，以前我写过关于此的文章，请见：http://t.csdn.cn/5oEAA

---

回过来，作为一名数学爱好者，再次庆祝一下这个数学节日，也算符合教科文组织确立本纪念日的目的：“为庆祝数学在生活中的美丽和重要性”。最后，让我们来共同欣赏一下 π 的独特魅力：

莱布尼茨级数 

 平方数倒数之和无穷级数

欧拉恒等式——5个常量构成“最美公式”，有理数无理数实数虚数融汇一体

双曲几何三角形面积公式

高斯-博内定理

等周不等式 

拉马努金“最丑”的数学公式

爱因斯坦广义相对论的核心方程：爱因斯坦场方程

海森堡不确定性原理是量子力学的一个重要原理 

霍金黑洞温度公式，除了有pi还包含了牛顿的万有引力常数（G）、普朗克常数（h）、光速（c）、以及玻尔兹曼常数（k）