【递归】入门基础，掌握这些优化技巧就够了

博客昵称：吴NDIR
个人座右铭：得之淡然，失之坦然
作者简介：喜欢轻音乐、象棋，爱好算法、刷题
其他推荐内容
计算机导论速记思维导图
五种排序算法
二分查找入门讲解
双指针思维模式基础

---

今天让我们聊一下递归吧！递归常用于二叉树遍历、搜索、数学运算、数据结构等领域的算法设计。

一、基本概念和应用

• 概念

递归是一种解决问题的思路或算法，是指函数自身调用自身的方式来实现某种功能。通俗点说，递归就是把原问题不断地分解成更小的子问题来求解，直到问题缩小到足够小，可以直接求解得到答案，这样就可以通过合并子问题的解来得到原问题的解。

1. 用递归模拟循环

逻辑图示：

• 代码示例

#include 

// 递归模拟循环计数器
void countdown(int n) {
  if (n <= 0) { // 基础情况（条件判断）
    return;
  } else { // 递归情况
    printf("%d\n", n);
    countdown(n-1);
  }
}

int main() {
  countdown(5); // 使用递归模拟循环
  return 0;
}

• 示例结果

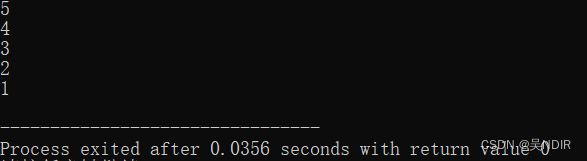
这样我们就简单使用递归算法了，主函数调用目标函数，目标函数设定条件。那我们使用递归可以解决哪些问题呢？这是个经典问题：使用递归实现阶乘

题目：输入一个整数n(n>=0)，求n的阶乘。
思路：根据阶乘的定义，如果n=0，则n的阶乘为1；否则，n的阶乘为n×(n-1)的阶乘。这里可以使用递归来求解n的阶乘。条件判断n>=0?

#include 

/* 递归求阶乘 */
int Factorial(int n)
{
    if (n == 0) {
        return 1;
    }
    else {
        return n * Factorial(n - 1);
    }
}

int main()
{
    int n;
    printf("请输入一个数：\n");
    scanf("%d", &n);
    printf("%d的阶乘是：%d\n", n, Factorial(n));
    return 0;
}

在主函数中，我们首先使用printf函数打印一个提示消息，提示用户输入一个整数。然后使用scanf函数读取用户输入的整数。最后，调用Factorial函数并打印结果。
函数首先判断n是否等于0，如果是，则返回1。否则，将n乘以Factorial(n - 1)的结果，然后返回该结果。这个递归调用一直持续到n等于0，然后递归返回，并返回最终的结果。

二、进阶应用

通常情况下，递归算法的时间和空间开销都比较大，因此在一些问题中需要注意算法效率和语言栈的溢出问题。在一些特定情况下，我们还需要对递归算法做一些优化。

1. 尾递归优化

尾递归是一种特殊的递归形式，指的是递归函数在每个递归调用的末尾调用自己。这种特殊的调用方式可以优化递归程序的时间复杂度和栈空间的使用。下面以斐波那契数列为引导。

非尾递归

/* 非尾递归 */
int fib1(int n) {
    if (n == 0 || n == 1) {
        return n;
    }
    else {
        return fib1(n - 1) + fib1(n - 2);
    }
}

尾递归

/* 尾递归 */
int fib2(int n, int f1, int f2) {
    if (n == 0) {
        return f1;
    }
    else {
        return fib2(n - 1, f2, f1 + f2);
    }
}

int main() {
    int n;
    printf("请输入一个数：\n");
    scanf("%d", &n);
    printf("第%d项斐波那契数列的值是：%d\n", n, fib2(n, 0, 1));
    return 0;
}

• 在尾递归的形式下，函数每次递归调用时只需更新参数即可，无需创建新的变量存储中间结果。这样可以减少每次递归调用的时间复杂度，也可以将递归函数转化为循环语句，从而避免了一些递归操作栈的消耗，解决了传统递归中可能遇到的栈溢出问题。

上述两个函数分别使用普通递归和尾递归来实现斐波那契数列的求解。假设我们求解斐波那契数列的第40项，由于斐波那契数列的前两项都是1，因此在计算过程中会有大量的重复计算。但是通过尾递归，我们只需要每次计算出下一项即可，无需再回溯上一个状态进行局部变量的更新，提高了程序的效率。

2. 分治递归

在使用常见的快速排序中就用到了分治递归的思想，具体查看博客 五种排序算法

我们在这也用另一个例子讲解：
题目描述：我们考虑计算一个整数数组的最大子序和，即对于长度为n的数组，要求出其中一段连续子序列的和最大值。

• 假设数组A中的元素范围很大，无法一次性计算所有子序列的和，需要采用一种分治的方式，将问题分成若干小问题，再将每个小问题求解的结果整合起来得到最终结果。具体思路如下：

1. 计算整个数组的和sum，如果sum为正，说明最大子序和一定包含数组的第一个元素和最后一个元素，否则最大子序和一定不包含最后一个元素，我们只需要考虑数组的前 n-1个元素。
2. 分解问题：通过数组中心元素将问题分成两个子问题，分别是左侧区间[low,mid] 和右侧区间[mid+1,high]。具体而言，我们递归地解决两个子问题，并计算出这两个子问题的最大子序和。
3. 合并问题：整合上述两个最大子序和分别存储的区间，找到跨越中心的最大子序和。这一步可以通过计算从中心元素向左和向右的连续子序列之和的最大值，并将它们加起来来实现。

#include 
#include 

#define MAX(a,b) ((a)>(b)?(a):(b))
#define MIN(a,b) ((a)<(b)?(a):(b))

/* 计算包含中心元素的最大子序和 */
static int MaxCrossingSum(int arr[], int low, int mid, int high) {
    int left_sum = INT_MIN;
    int right_sum = INT_MIN;
    int sum = 0;
    for (int i = mid; i >= low; --i) {
        sum += arr[i];
        if (sum > left_sum) {
            left_sum = sum;
        }
    }
    sum = 0;
    for (int i = mid + 1; i <= high; ++i) {
        sum += arr[i];
        if (sum > right_sum) {
            right_sum = sum;
        }
    }
    return left_sum + right_sum;
}

/* 计算最大子序和 */
static int MaxSubArraySum(int arr[], int low, int high) {
    if (low == high) {
        return arr[low];
    }
    int mid = (low + high) / 2;
    int left_sum = MaxSubArraySum(arr, low, mid);
    int right_sum = MaxSubArraySum(arr, mid + 1, high);
    int crossing_sum = MaxCrossingSum(arr, low, mid, high);
    return MAX(MAX(left_sum, right_sum), crossing_sum);
}

int main() {
    int arr[] = { -2, -5, 6, -2, -3, 1, 5, -6 };//例子
    int n = sizeof(arr) / sizeof(arr[0]);
    printf("最大连续子序和为：%d\n", MaxSubArraySum(arr, 0, n - 1));
    return 0;
}

使用递归的方式将问题分成两部分，分别递归求解并得到左侧子问题的最大子序和、右侧子问题的最大子序和以及跨越中心元素的最大子序和，并将这三个结果中的最大值作为整个问题的结果返回。这样，我们就通过分治法优化了递归算法，避免了原问题的重复计算，提高了算法效率。