LeetCode 刷题之 BFS 广度优先搜索【Python实现】
1. BFS 算法框架
BFS:用来搜索 最短路径 比较合适,如:求二叉树最小深度、最少步数、最少交换次数,一般与 队列 搭配使用,空间复杂度比DFS大很多DFS:适合搜索全部的解,如:寻找最短距离,一般与 栈 搭配使用
def BFS(start, target):
"""计算从 start 到 target 的最近距离"""
q = [] # 队列,先进先出
visited = {} # 避免走回头路
q.append(start) # 将起点加入队列
visited.add(start)
step = 0 # 记录扩散步数
while q:
for i in range(len(q)):
cur = q.pop()
# 判断是否达到终点
if cur == target:
return step
# 将 cur 相邻的节点加入队列
for j in cur.adj():
if j not in visited:
q.insert(0, j) # 队列:先进先出
visited.add(j)
# 更新步数
step += 1
2. 二叉树的最小深度
111. 二叉树的最小深度
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明:叶子节点是指没有子节点的节点。
输入:root = [3,9,20,null,null,15,7]
输出:2
示例 2:
输入:root = [2,null,3,null,4,null,5,null,6]
输出:5
提示:
树中节点数的范围在 [0, 105] 内
-1000 <= Node.val <= 1000
题解:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def minDepth(self, root: TreeNode) -> int:
if not root:return 0
q = [root]
step = 1
while q:
size = len(q)
for i in range(size):
node = q.pop(0)
# 判断是否达到终点,结束条件
if node.left == None and node.right == None:
return step
# 将相邻节点添加到队列
if node.left != None:
q.append(node.left)
if node.right != None:
q.append(node.right)
# 更新步数
step += 1
return step
if __name__ == '__main__':
# root = [3,9,20,null,null,15,7]
root = TreeNode(3)
node1 = TreeNode(9)
node2 = TreeNode(20)
node3 = TreeNode(15)
node4 = TreeNode(7)
root.left = node1
root.right = node2
node2.left = node3
node2.right = node4
s = Solution()
print(s.minDepth(root))
3. 二叉树的层序遍历
102. 二叉树的层序遍历
给你二叉树的根节点 root ,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。
示例 1:
输入:root = [3,9,20,null,null,15,7]
输出:[[3],[9,20],[15,7]]
示例 2:
输入:root = [1]
输出:[[1]]
示例 3:
输入:root = []
输出:[]
提示:
树中节点数目在范围 [0, 2000] 内
-1000 <= Node.val <= 1000
题解:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def levelOrder(self, root: TreeNode) -> List[List[int]]:
if root == None:
return []
q = [root]
res = []
while q:
level = [] # 记录每层节点的值
for i in range(len(q)):
node = q.pop()
level.append(node.val)
# 说明该节点没有左右节点了
if node.left == None and node.right == None:
continue
if node.left != None:
q.insert(0, node.left)
if node.right != None:
q.insert(0, node.right)
# 将每层的结果添加到 res
res.append(level)
return res
4. 打开转盘锁
752. 打开转盘锁
你有一个带有四个圆形拨轮的转盘锁。每个拨轮都有10个数字: '0', '1', '2', '3', '4', '5', '6', '7', '8', '9' 。每个拨轮可以自由旋转:例如把 '9' 变为 '0','0' 变为 '9' 。每次旋转都只能旋转一个拨轮的一位数字。
锁的初始数字为 '0000' ,一个代表四个拨轮的数字的字符串。
列表 deadends 包含了一组死亡数字,一旦拨轮的数字和列表里的任何一个元素相同,这个锁将会被永久锁定,无法再被旋转。
字符串 target 代表可以解锁的数字,你需要给出解锁需要的最小旋转次数,如果无论如何不能解锁,返回 -1 。
示例 1:
输入:deadends = ["0201","0101","0102","1212","2002"], target = "0202"
输出:6
解释:
可能的移动序列为 "0000" -> "1000" -> "1100" -> "1200" -> "1201" -> "1202" -> "0202"。
注意 "0000" -> "0001" -> "0002" -> "0102" -> "0202" 这样的序列是不能解锁的,
因为当拨动到 "0102" 时这个锁就会被锁定。
示例 2:
输入: deadends = ["8888"], target = "0009"
输出:1
解释:把最后一位反向旋转一次即可 "0000" -> "0009"。
示例 3:
输入: deadends = ["8887","8889","8878","8898","8788","8988","7888","9888"], target = "8888"
输出:-1
解释:无法旋转到目标数字且不被锁定。
提示:
1 <= deadends.length <= 500
deadends[i].length == 4
target.length == 4
target 不在 deadends 之中
target 和 deadends[i] 仅由若干位数字组成
题解:
class Solution:
def openLock(self, deadends: List[str], target: str) -> int:
if target == "0000":
return 0
visited = {"0000"} # 记录已经穷举过的密码,防止走回头路
q = ["0000"]
step = 0 # 步数
while q:
for i in range(len(q)):
num = q.pop()
# 若刚好是目标就退出
if num == target:
return step
if num in deadends:
continue
# 拨动密码锁,将一个节点的未遍历相邻节点加入队列
for j in range(4):
# 向上拨动
up = self.plus_one(num, j)
# 向下拨动
down = self.minus_one(num, j)
# 若已经访问过则不添加到 visited
if up not in visited:
q.insert(0, up)
visited.add(up)
if down not in visited:
q.insert(0, down)
visited.add(down)
# 增加步数
step += 1
return -1
def plus_one(self, num, j):
a = list(num)
if a[j] == "9":
a[j] = "0"
else:
a[j] = str(int(a[j]) + 1)
return "".join(a)
def minus_one(self, num, j):
a = list(num)
if a[j] == "0":
a[j] = "9"
else:
a[j] = str(int(a[j]) -1)
return "".join(a)
参考:BFS 算法框架套路详解
5. 钥匙和房间
841. 钥匙和房间
有 n 个房间,房间按从 0 到 n - 1 编号。最初,除 0 号房间外的其余所有房间都被锁住。你的目标是进入所有的房间。然而,你不能在没有获得钥匙的时候进入锁住的房间。
当你进入一个房间,你可能会在里面找到一套不同的钥匙,每把钥匙上都有对应的房间号,即表示钥匙可以打开的房间。你可以拿上所有钥匙去解锁其他房间。
给你一个数组 rooms 其中 rooms[i] 是你进入 i 号房间可以获得的钥匙集合。如果能进入 所有 房间返回 true,否则返回 false。
示例 1:
输入:rooms = [[1],[2],[3],[]]
输出:true
解释:
我们从 0 号房间开始,拿到钥匙 1。
之后我们去 1 号房间,拿到钥匙 2。
然后我们去 2 号房间,拿到钥匙 3。
最后我们去了 3 号房间。
由于我们能够进入每个房间,我们返回 true。
示例 2:
输入:rooms = [[1,3],[3,0,1],[2],[0]]
输出:false
解释:我们不能进入 2 号房间。
提示:
n == rooms.length
2 <= n <= 1000
0 <= rooms[i].length <= 1000
1 <= sum(rooms[i].length) <= 3000
0 <= rooms[i][j] < n
所有 rooms[i] 的值 互不相同
题解:
class Solution:
def canVisitAllRooms(self, rooms: List[List[int]]) -> bool:
visited = {0} # 记录已经穷举过的钥匙,防止走回头路
queue = [0]
while queue:
index_keys = queue.pop()
for i in rooms[index_keys]:
if i not in visited:
visited.add(i)
queue.insert(0, i)
return len(visited) == len(rooms)
这个题还可以用 DFS,只需将 queue.insert 换成 queue.append 即可
参考:7行DFS 8行BFS 两种方法 三种实现 超详细趣味0基础解 Python
6. BFS 遍历图
# -- coding: utf-8 --
def bfs(_graph, s):
"""
BFS 遍历 图
:param _graph: 图
:param s: 从哪个点开始遍历
:return:
"""
q = [s]
visited = {s}
while q:
vertex = q.pop()
nodes = _graph[vertex]
for node in nodes:
if node not in visited:
visited.add(node)
q.insert(0, node)
print(vertex)
if __name__ == '__main__':
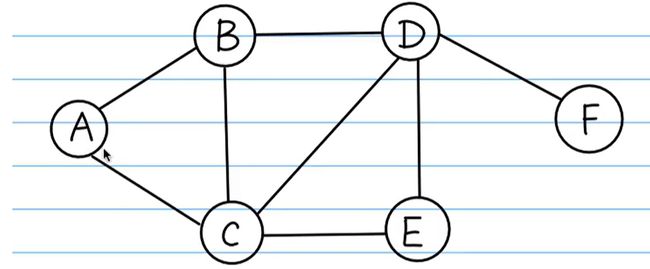
# 图可以抽象为一个字典,key 表示当前节点,value 为该节点的下个节点集合
graph = {
"A": ["B", "C"],
"B": ["A", "C", "D"],
"C": ["A", "B", "D", "E"],
"D": ["B", "C", "E", "F"],
"E": ["C", "D"],
"F": ["D"],
}
bfs(graph, "A") # 从 A 点开始,输出 A、B、C、D、E、F
参考:[Python] BFS和DFS算法(第1讲)