数学建模:火箭发生升空模型——基于matlab语言
基于教材:《数学建模》第五版
仅是为了个人记录,也为了在有需要的情况下帮到大家,排版可能略显拉跨,但代码以及实验结果均正确!!!
如果帮到你了,请动手点个小赞吧,
一、不考虑空气阻力的简单模型
- 问题描述:设小型火箭初始质量为m0=1600kg,其中包括m1=1080kg燃料,火箭从地面垂直向上发射时,燃料以r=18kg/s的速率燃烧,对火箭产生F=2000N的恒定推力,燃料燃尽后火箭继续上升,知道达到最高点,因为火箭上升高度与地球半径相比很小,所以可认为整个过程中受到的地球引力不变,重力加速度取9.8kg/s2,建立火箭上升高度、速度和加速度随时间变化的数学模型,给出燃料燃尽时喉间的高度、速度和加速度以及火箭达到最高点的时间和高度;
- 问题分析:在求解的时候设计到三个结果:路程、速度以及加速度;我们通过牛顿定律知道当燃料燃尽时仍然会有速度,仍然会继续上升,因此我们可以将整个过程分为两个阶段:有燃料和没有燃料;
- 求解基本模型:(m0-rt)a=F-(m0-rt)g; (m0-m1)a=-(m0-m1)g;
v= -g(t-t1)+v(t1); x(t)=-(g(t-t1)^2)/2+v(t1)(t-t1)+x(t1); - 求解代码
%火箭发射升空--不考虑空气阻力
clc
clear
% 已知条件:初始质量m0=1600,燃料m1=1080,速度r=18
% 推力F=27000,重力加速度g=9.8
%第一阶段是有燃料,使用方程(3)-(5),t(max)=60s
g=9.8;
m0=1600;
m1=1080;
F=27000;
r=18;
t1=0:60;
%关闭科学计数法:并只显示一位小数
format short g
a1=-g+F./(m0-r.*t1)
v1=-g.*t1+F/r.*log(m0./(m0-r.*t1))
%路程
temp1=(F.*(m0-r.*t1).*(log(m0-r.*t1)-1))./(r.*r);
temp2=((F.*log(m0)).*t1)./r;
temp3=(F.*m0.*(log(m0)-1))./(r.*r);
x1=-(g.*t1.*t1./2)+temp1+temp2-temp3
%第二阶段:没有燃料
tlast=60;
xlast=x1(61);
vlast=v1(61);
t2=60:(vlast/g)+60;
a2=-g;
a2=-g+zeros(1,113);
v2=-g.*(t2-tlast)+vlast
x2=-(g.*(t2-tlast).*(t2-tlast))./2+vlast.*(t2-tlast)+xlast
%路程
plot(t1,x1,'b',t2,x2,'b')
grid on
%速度
plot(t1,v1,'b',t2,v2,'b');
grid on
%加速度
line([60,60],[-9.8,a1(61)],'Color','b','LineWidth',1)
hold on
plot(t1,a1,'b',t2,a2,'b');
grid on
5.最终结果———路程x(t)

6.最终结果——速度v(t)

二、考虑空气阻力:
-
原因:运动的物体都会受到空气的阻力,运动速度越大阻力就越大,但二者之间没有确定的数量关系,按照相关知识和经验。低速时阻力与速度的平方成正比,比例系数记为k,于是在考虑空气阻力情况下方程(1)、(2)应该改写;
-
模型的建立:我们就取阻力系数k=0.3kg/m;改写后的两个主要方程:
(m0-rt)a=F-kv^2-(m0-rt)g;
(m0-m1)a=-kx^2-(m0-m1)g; -
求解方法:这里存在微分方程的求解,我们就需要使用matlab中求解微分方程的函数ode45(),在求解的时候我们需要创建一个功能函数文件作为参数;同样,在求解的时候我们需要将整个过程划分为有阻力和没有阻力的阶段,然后依次进行求解。
-
主函数代码:
%有阻力的情况下
[t1,y1]=ode45(@Windfun1,[0 60],[0;0]);
%路程
plot(t1,y1(:,1))
grid on
%速度
plot(t1,y1(:,2));
grid on
%加速度
g=9.8;
m0=1600;
m1=1080;
F=27000;
r=18;
k=0.3;
a1=(F-(k.*y1(:,2).*y1(:,2))-(m0-r.*t1).*g)./(m0-r.*t1);
plot(t1,a1)
grid on
% 第二个阶段
init1=y1(end,1);
init2=y1(end,2);
[t2,y2]=ode45(@Windfun2,[60 80],[init1;init2]);
% 路程
plot(t1,y1(:,1),t2,y2(:,1))
grid on
% 速度
plot(t1,y1(:,2),t2,y2(:,2));
grid on
%加速度
a2=((-k.*y2(:,2).*y2(:,2))-(m0-m1).*g)./(m0-m1);
plot(t1,a1,'b',t2,a2,'b')
hold on
line([60 60],[a1(end) a2(1)]);
grid on
5.功能函数文件1(有燃料阶段)代码----Windfun1.m
function y=Windfun1(t,x)
g=9.8;
m0=1600;
F=27000;
r=18;
k=0.3;
y=[x(2);
(F-(k.*x(2).*x(2))-(m0-r.*t).*g)./(m0-r.*t)];
end
6.功能函数文件2(没有燃料)代码----Windfun2
function y=Windfun2(t,x)
g=9.8;
m0=1600;
m1=1080;
k=0.3;
y=[x(2);
(-k.*(x(2).*x(2))-(m0-m1).*g)./(m0-m1)];
end
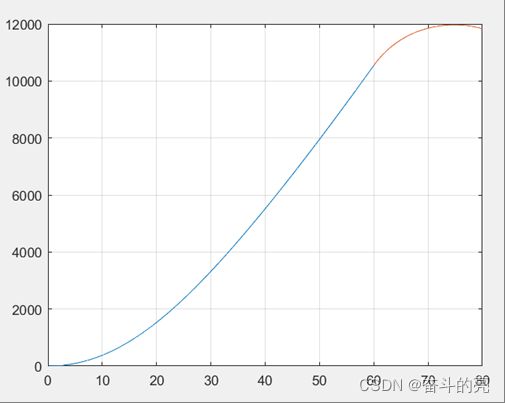
7.求解结果——路程

8.求解结果——速度

9求解结果——加速度

三、提示火箭的方法1:增加燃料
- 问题描述:要提升火箭的上升高度方法之一:增加火箭的燃料,即燃料增加一倍;m1=2160kg,m0=2680kg,时间自然变为t=120s;
- 解决方案:我们只需要在有阻力的功能函数文件中将火箭质量以及燃料质量一起修改为对应值即可得到相应的结果;
- 主文件代码
[t1,y1]=ode45(@Developfun1,[0 120],[0;0]);
%路程
plot(t1,y1(:,1))
grid on
%速度
plot(t1,y1(:,2));
grid on
%加速度
g=9.8;
m0=2680;
m1=2160;
F=27000;
r=18;
k=0.3;
a1=(F-(k.*y1(:,2).*y1(:,2))-(m0-r.*t1).*g)./(m0-r.*t1);
plot(t1,a1)
grid on
%后半程
init1=y1(end,1);
init2=y1(end,2);
[t2,y2]=ode45(@Developfun2,[120 140],[init1;init2]);
% 路程
plot(t1,y1(:,1),t2,y2(:,1))
grid on
% 速度
plot(t1,y1(:,2),t2,y2(:,2));
grid on
%加速度
a2=((-k.*y2(:,2).*y2(:,2))-(m0-m1).*g)./(m0-m1);
plot(t1,a1,'b',t2,a2,'b')
hold on
line([120 120],[a1(end) a2(1)]);
grid on
4.功能函数文件1—Developfun1.m
function y=Developfun1(t,x)
g=9.8;
m0=2680;
F=27000;
r=18;
k=0.3;
y=[x(2);
(F-(k.*x(2).*x(2))-(m0-r.*t).*g)./(m0-r.*t)];
End
5.功能函数文件2—Developfun2.m
function y=Develop2fun1(t,x)
g=9.8;
m0=1600;
m1=1080;
F=54000;
r=18;
k=0.3;
y=[x(2);
(F-(k.*x(2).*x(2))-(m0-r.*t).*g)./(m0-r.*t)];
End
四、提升火箭方法2:增加推力
1.问题描述:将燃料的推力F改为F=54000;
2.主函数文件代码
%改装2:增加动力,其他因素不变
[t1,y1]=ode45(@Develop2fun1,[0 60],[0;0]);
%路程
plot(t1,y1(:,1))
grid on
%速度
plot(t1,y1(:,2));
grid on
%加速度
g=9.8;
m0=1600;
m1=1080;
F=54000;
r=18;
k=0.3;
a1=(F-(k.*y1(:,2).*y1(:,2))-(m0-r.*t1).*g)./(m0-r.*t1);
plot(t1,a1)
grid on
% 阶段二
init1=y1(end,1);
init2=y1(end,2);
[t2,y2]=ode45(@Develop2fun2,[60 80],[init1;init2]);
% 路程
plot(t1,y1(:,1),t2,y2(:,1))
grid on
% 速度
plot(t1,y1(:,2),t2,y2(:,2));
grid on
%加速度
a2=((-k.*y2(:,2).*y2(:,2))-(m0-m1).*g)./(m0-m1);
plot(t1,a1,'b',t2,a2,'b')
hold on
line([60 60],[a1(end) a2(1)]);
grid on
3.功能函数文件1——Develop2fun1
function y=Develop2fun1(t,x)
g=9.8;
m0=1600;
m1=1080;
F=54000;
r=18;
k=0.3;
y=[x(2);
(F-(k.*x(2).*x(2))-(m0-r.*t).*g)./(m0-r.*t)];
end
4.功能函数文件2——Develop2fun2
function y=Develop2fun2(t,x)
g=9.8;
m0=1600;
m1=1080;
k=0.3;
y=[x(2);
(-k.*(x(2).*x(2))-(m0-m1).*g)./(m0-m1)];
end
6.求解结果——速度