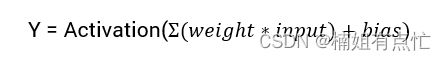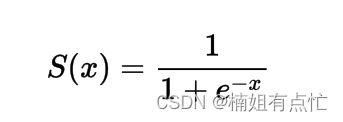2023.4.1 激活函数-Python实现
什么是激活函数？
激活函数是控制神经网络输出的数学函数。激活函数有助于确定是否要激活神经元。
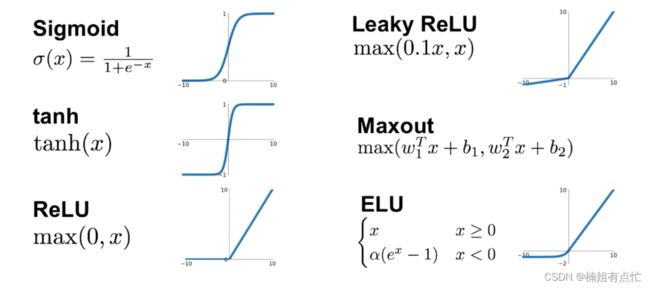
一些流行的激活函数是：
- Sigmoid
- ReLU
- Leaky ReLU
- Tanh
- Maxout
- ELU
激活负责为神经网络模型的输出添加非线性。没有激活函数，神经网络只是一个线性回归。
计算神经网络输出的数学方程式为：
sigmoid 激活函数
sigmoid 函数的公式
在数学上，sigmoid激活函数表示为：
在 Python 中实现 Sigmoid 函数
在python中的函数定义如下：
import numpy as np
def sig(x):
return 1/(1 + np.exp(-x))
使用 Python 绘制 Sigmoid 函数
使用python绘制sigmoid激活函数
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-10,10,50)
p = sig(x)
plt.xlabel("x")
plt.ylabel("Sigmoid(x)")
plt.plot(x, p)
plt.show()
我们可以看出来输出介于0到1之间。
通过观察图片，我们不难看出sigmoid 函数的特点：
对于中间区域，Y值对X值变化的影响非常大；
对于末端区域，Y 值对 X 值变化的响应非常小。
当然，对于末端区域，这导致了一个称为消失梯度问题的问题。
消失梯度减慢了学习过程，因此是不可取的。
于是为了克服这个问题，我们想出来了一些替代方案：ReLu激活函数和Leaky ReLu 激活函数
ReLu激活函数
ReLu(Rectified Linear Activation Function)是深度学习领域最常见的激活函数选择。ReLu提供了最先进的结果，同时在计算上非常高效。
ReLu激活函数的基本概念如下：
如果输入是负数那么返回0，否则按照原样返回。
ReLu激活函数的公式
我们可以用数学方式表示如下：
在 Python 中实现 ReLu 函数
我们将使用内置的 max 函数来实现它
def relu(x):
return max(0.0, x)
使用 Python 绘制 ReLu 函数
使用python绘制ReLu激活函数
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-10,10,51)
y = []
for i in x:
p = relu(i)
y.append(p)
plt.xlabel("x")
plt.ylabel("ReLu(x)")
plt.plot(x, y)
plt.show()
ReLu函数的梯度
让我们来看一下 ReLu函数的梯度（导数）是多少。
f’(x) = 1, x≥0
= 0, x<0
我们可以看到，对于小于零的 x 值，梯度为0。这意味着某些神经元的权重和偏差没有更新。这可能是训练过程中的一个问题。
为了克服这个问题，我们有 Leaky ReLu 函数。接下来我们就来了解一下。
Leaky ReLu 函数
Leaky ReLu 函数是常规ReLu函数的即兴创作。为了解决负值的零梯度问题，Leaky ReLu 为负输入提供了极小的x线性分量。
在数学上，我们可以将 Leaky ReLu 表示为：
f(x)= 0.01x, x<0
= x, x>=0
数学上：
- f(x)=1 (x<0)
- (αx)+1 (x>=0)(x)
这里 a 是一个小常数，就像我们上面采用的 0.01 一样。
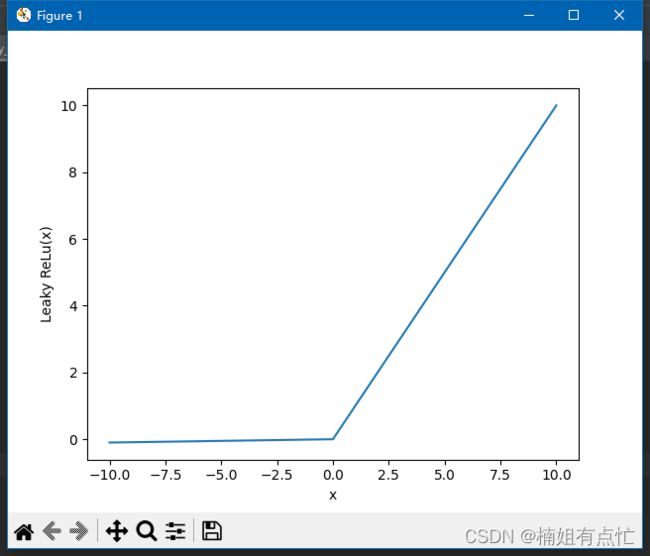
在图形上它可以显示为：
在 Python 中实现 Leaky ReLu 函数
Leaky ReLu 的实现如下：
def relu(x):
if x < 0:
return 0.01 * x
else:
return x
使用 Python 绘制 Leaky ReLu 函数
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-10, 10, 51)
y = []
for i in x:
p = relu(i)
print(p)
y.append(p)
plt.xlabel("x")
plt.ylabel("Leaky ReLu(x)")
plt.plot(x, y)
plt.show()
Leaky ReLu函数的梯度
让我们计算 Leaky ReLu 函数的梯度。梯度可以是:
f’(x) = 1, x>=0
= 0.01, x<0
在这种情况下，负输入的梯度是非零的。这意味着所有的神经元都将被更新。
Tanh 激活函数
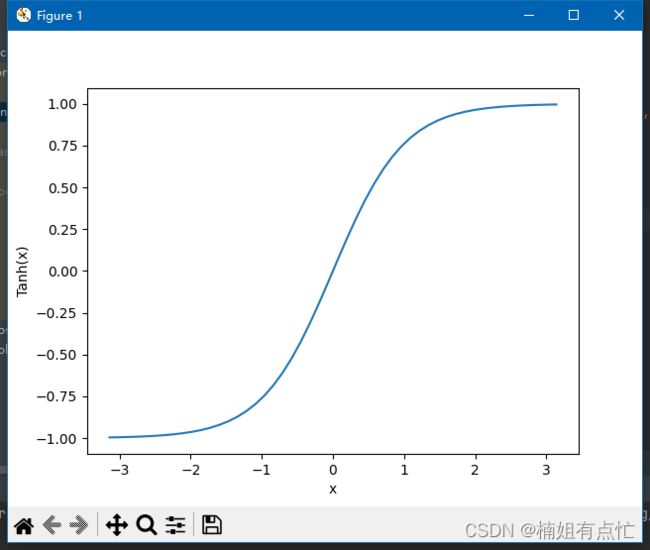
tanh 也类似于 logistic sigmoid 但更好。tanh 函数的取值范围是（-1 到 1）。tanh 也是 S 形的（s 形）。
优点是负输入将映射为强负，零输入将映射到 tanh 图中的零附近。
函数是可微分的。
该函数是单调的，而其导数不是单调的。
Tanh激活函数的公式
我们可以用数学方式表示如下：
在 Python 中实现 Tanh 函数
我们将使用内置的 max 函数来实现它
def tanh(x):
return math.tanh(x)
使用 Python 绘制 Tanh 函数
使用python绘制ReLu激活函数
import math
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-math.pi, math.pi, 50)
y = []
for i in x:
p = tanh(i)
y.append(p)
plt.xlabel("x")
plt.ylabel("Tanh(x)")
plt.plot(x, y)
plt.show()
