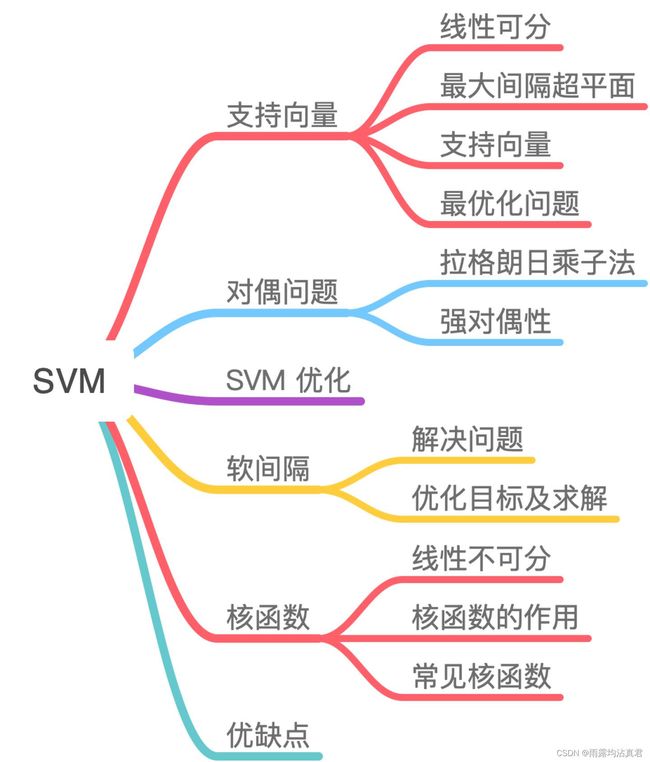
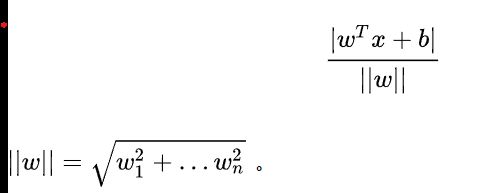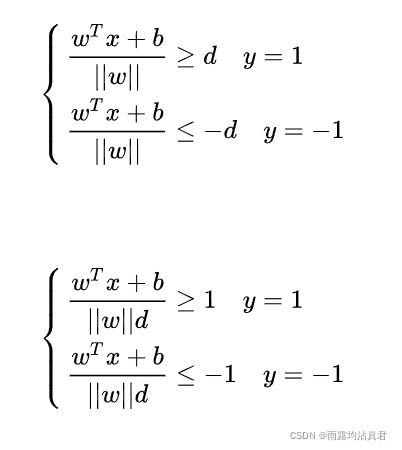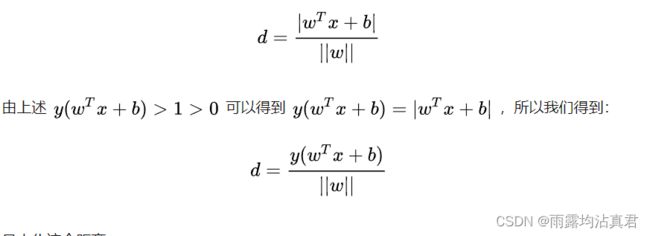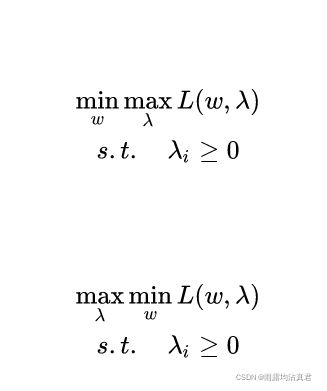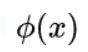机器学习的十大经典算法——SVM
1线性可分
什么叫做线性可分?
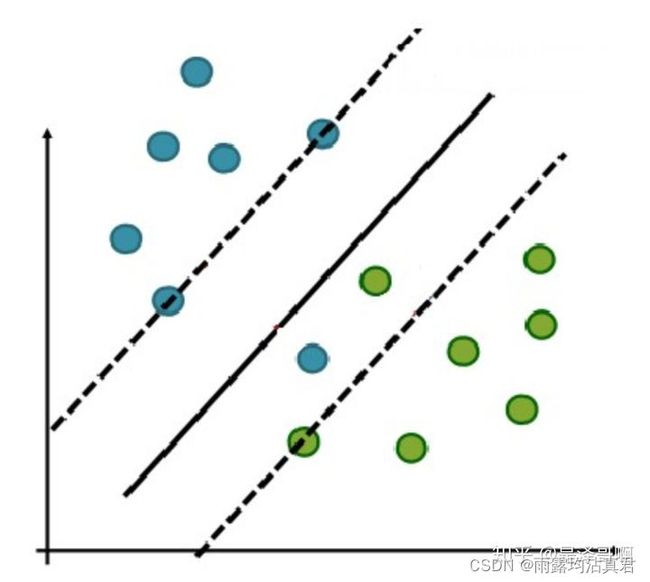
就如这个图片所以显示,就是二个不同种类的点,被一条直线所分
1.2 最大间隔超平面
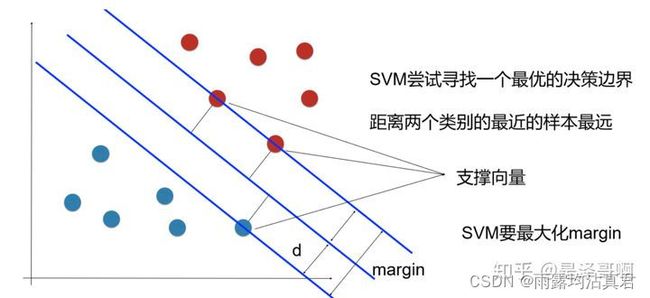
通俗易懂的来说,就是用线性可分的二种不同的类型点,然后用一条直线分开的那天直线,然后用两条平行于这个直线的两条直线,将二个不同种类的点分的更加开一点,这两条直线围成的平面叫做超平面
为了使这个超平面更具鲁棒性,我们会去找最佳超平面,以最大间隔把两类样本分开的超平面,也称之为最大间隔超平面。
- 两类样本分别分割在该超平面的两侧;
- 两侧距离超平面最近的样本点到超平面的距离被最大化了。
样本中距离超平面最近的那些点叫做支持向量
1.4 SVM 最优化问题
SVM 想要的就是找到各类样本点到超平面的距离最远,也就是找到最大间隔超平面。任意超平面可以用下面这个线性方程来描述:
![]()
如此可知,点到这条直线的距离,我们在高中就知道了,所以这里就不写出来
在多维的空间中,扩展到 n 维空间后,点x到直线的距离:
支持向量距离超平面最近,相当于其他点来说;
如图所示,根据支持向量的定义我们知道,支持向量到超平面的距离为 d,其他点到超平面的距离大于 d。
由此可以推出下面的公式:
上面的公式把d移动到左边如此,公式下面的wd的那块, 是正数,我们暂且令它为 1(之所以令它等于 1,是为了方便推导和优化,且这样做对目标函数的优化没有影响),故: 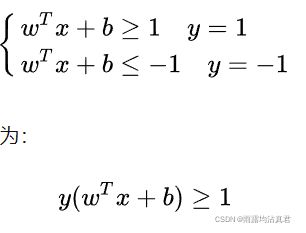
把y移动到公式中,由于y只有二个值:1,-1;所以移动过去没有影响;
每个支持向量到超平面的距离可以写为:
这里可能有人感觉疑惑,这两个公式相等,是因为y的取值只有两个(1or -1),然而另外一个是因为距离的方向,所以有正负之分,所以二个是相等的;
2. 对偶问题
2.1 拉格朗日乘数法
2.1.1 等式约束优化问题
高等数学下中有一个拉格朗日公式就是这样一个问题
我们将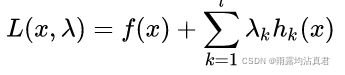 命名为L(x, 拉姆达)函数,其中拉姆达没有非负要求;
命名为L(x, 拉姆达)函数,其中拉姆达没有非负要求;
根据集体问题,具体分析,大部分时候取极点,等式优化下,有L个拉姆达,把x和拉姆达一视同仁,也可以看做优化参数,所以一个有k+l个优化参数
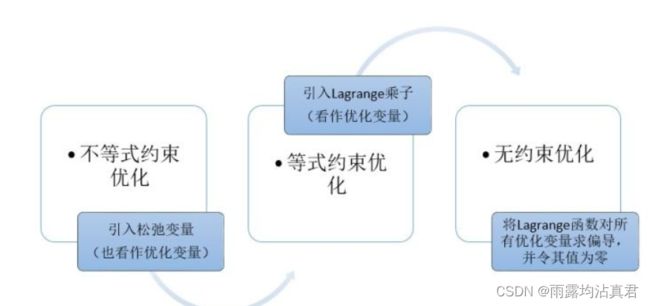
2.1.2 不等式约束优化问题
接下来,我们应该说不等式优化,可以将不等式转为等式,同时加上松弛变量,这个也是一个优化参数,
2.2 强对偶性
两个函数成对偶,最大的里面挑出来的最小的也要比最小的里面挑出来的最大的要大。这关系实际上就是弱对偶关系,而强对偶关系是当等号成立时,最大的里面挑出来的最小的等于最小的里面挑出来的最大的,如果 ![]() 是凸优化问题,强对偶性成立,kkt是强对偶性的充要条件。
是凸优化问题,强对偶性成立,kkt是强对偶性的充要条件。
这里简单说一下kkt是什么:
KKT条件是针对含有不等式约束的优化问题的,
就是好几个等式组成一个方程组,然后就是在这个方程组围成的面积中里面取的最优的解,一般来说就是,用边缘的点是最优的解
3. SVM 优化
4. 软间隔
在实际生活中,不可能出现特别完美的数据,大部分都是带有一些噪声,所以这里介绍一下软间隔 :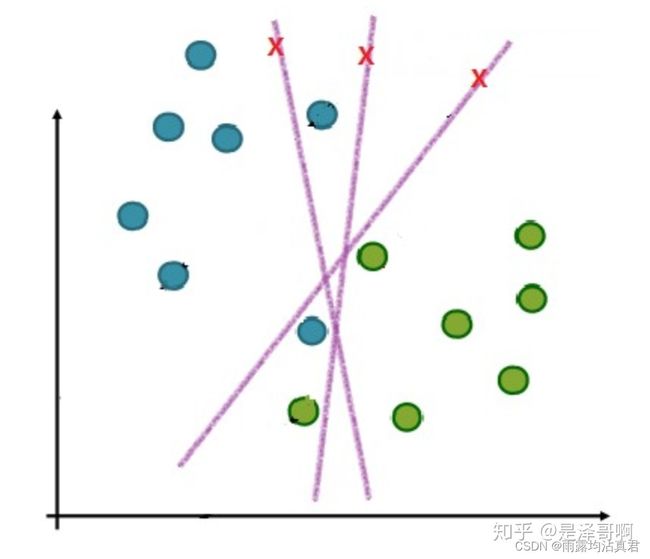
于是我们就有了软间隔,相比于硬间隔的苛刻条件,我们允许个别样本点出现在间隔带里面,比如:
我们允许部分样本点不满足约束条件:
为了度量这个间隔软到何种程度,我们为每个样本引入一个松弛变量 ![]() , 令
, 令 ![]() ,且
,且 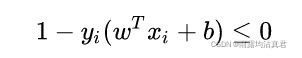 。对应如下图所示:
。对应如下图所示: 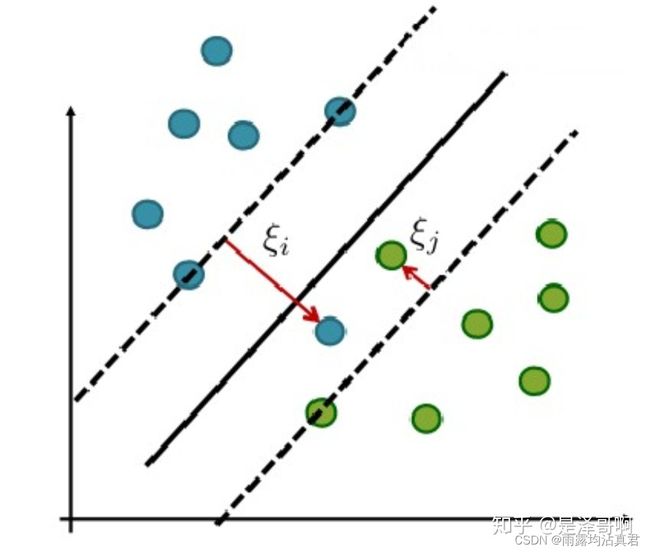
4.2 优化目标及求解
增加软间隔后我们的优化目标变成了:
5. 核函数
5.1 线性不可分
我们刚刚讨论的硬间隔和软间隔都是在说样本的完全线性可分或者大部分样本点的线性可分。
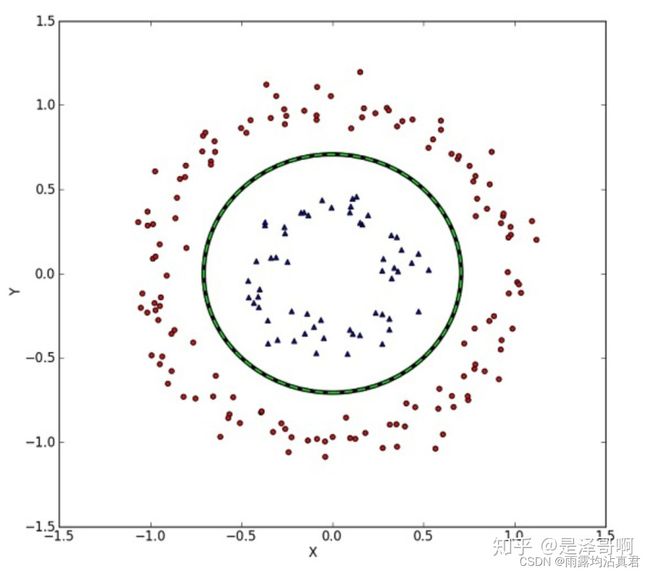
但我们可能会碰到的一种情况是样本点不是线性可分的,比如
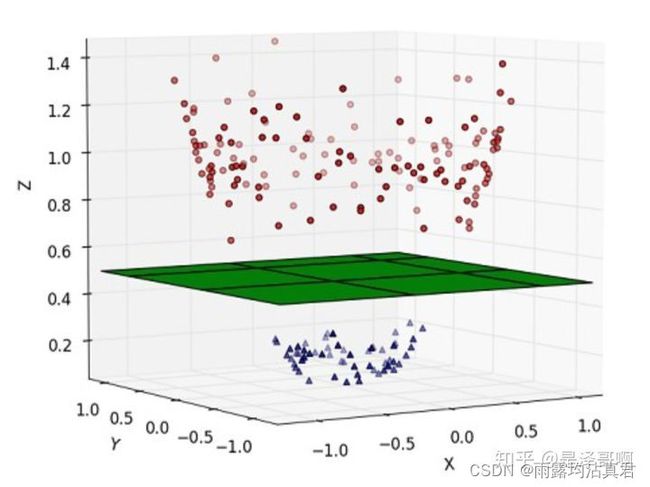
这种情况的解决方法就是:将二维线性不可分样本映射到高维空间中,让样本点在高维空间线性可分,比如
对于在有限维度向量空间中线性不可分的样本,我们将其映射到更高维度的向量空间里,再通过间隔最大化的方式,学习得到支持向量机,就是非线性 SVM。
我们用 x 表示原来的样本点,用 ![]() 表示 x 映射到特征新的特征空间后到新向量。那么分割超平面可以表示为:
表示 x 映射到特征新的特征空间后到新向量。那么分割超平面可以表示为: ![]() 。
。
对于非线性 SVM 的对偶问题就变成了:
这里说明一下,线性SVM和非线性SVM的区别:
5.2 核函数的作用
我们不禁有个疑问:只是做个内积运算,为什么要有核函数的呢?
这是因为低维空间映射到高维空间后维度可能会很大,如果将全部样本的点乘全部计算好,这样的计算量太大了。
其中常用的核函数:
其中就高斯核函数,需要调参数;
6. 优缺点
6.1 优点
- 有严格的数学理论支持,可解释性强,不依靠统计方法,从而简化了通常的分类和回归问题;
- 能找出对任务至关重要的关键样本(即:支持向量);
- 采用核技巧之后,可以处理非线性分类/回归任务;
- 最终决策函数只由少数的支持向量所确定,计算的复杂性取决于支持向量的数目,而不是样本空间的维数,这在某种意义上避免了“维数灾难”。
6.2 缺点
- 训练时间长。当采用 SMO 算法时,由于每次都需要挑选一对参数,因此时间复杂度为
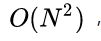 ,其中 N 为训练样本的数量;
,其中 N 为训练样本的数量; - 当采用核技巧时,如果需要存储核矩阵,则空间复杂度为
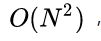 ;
; - 模型预测时,预测时间与支持向量的个数成正比。当支持向量的数量较大时,预测计算复杂度较高。
因此支持向量机目前只适合小批量样本的任务,无法适应百万甚至上亿样本的任务。