算法与数据结构——c语言描述01：分治、求最大公约数、快速求幂

0. 介绍

由于工作和学习中上用不到，在算法和数据结构方面的基础基本没有，而由于要考公司的c语言工作级认证，发现没有这方面的知识是完全考不上的，所以回过头来学习算法和数据结构，书就直接上Mark Allen Weiss的《数据结构与算法分析——C语言描述》了，以下是一些自己写的例程，希望可以作一个参考。

1. 数学基础

几个基本定义：

• 如果存在正常数c和n₀使得当N>=n₀时，T(N) <= cf(N)，则记为T(N) = O(f(N))
• 如果存在正常数c和n₀使得当N>=n₀时，T(N) >= cg(N)，则记为T(N) = Ω(g(N))
• T(N) = Θ(h(N))，当且仅当T(N) = O(h(N))，且T(N) = Ω(h(N))
• 如果T(N) = O(p(N))，且T(N / Θ(p(N))，则T(N) = o(p(N)

2. 要分析的问题

2.2 最大子序列和问题

给定整数A₁，A₂，…，A_N，求A_i+…+A_k的最大值，其中1 <= i <= k <= N。

对于不同时间复杂度的软件耗时如下图所示：

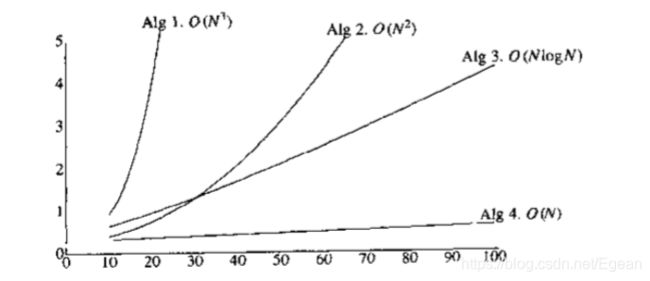
下面用分治算法实现该题，其时间复杂度为O(NlogN)。分治算法是将数组分为左半部分和右半部分，那么最大子序列必定出现在左边、右边或者横跨左右两边，如果是前两种情况，那么需要继续递归，寻找左边或右边的最大子序列，最后和第三种情况比较，其代码实现如下：

/*
 * 分治算法测试，例题为求最大子序列和，如：-7，2，9，18，-10，3，-6，5
 */

#include 
#include "common.h"
/* 计算从left到right的最大子序列 */
int max_sub_sum(int *arr, int left, int right)
{
    int medium = (left + right) / 2;
    int left_max, right_max;
    int i, left_max_medium, right_max_medium;
    int sum = 0;

    if (left == right) {
        return arr[left];
    }

    left_max = max_sub_sum(arr, left, medium);
    right_max = max_sub_sum(arr, medium + 1, right);

    /* 横跨左右两部分的最大值 */
    left_max_medium = arr[medium];  // 左边包含左边界的最大值
    for (i = medium; i >= left; i--) {
        sum += arr[i];
        if (sum > left_max_medium) {
            left_max_medium = sum;
        }
    }

    sum = 0;
    right_max_medium = arr[medium + 1]; // 右边包含右边界的最大值
    for (i = medium + 1; i <= right; i++) {
        sum += arr[i];
        if (sum > right_max_medium) {
            right_max_medium = sum;
        }
    }

    return max3(left_max, right_max, left_max_medium + right_max_medium);
}

int main(void)
{
    int test_arr[] = {-7, 2, 9, 18, -10, 3, -6, 5};
    int test_arr2[] = {4, -3, 5, -1, 2, 6, -2};
    int result = max_sub_sum(test_arr2, 0, sizeof(test_arr2) / sizeof(int) - 1);

    printf("%d\n", result);

    return 0;
}

其中common模块定义了一些常用宏定义，其实现如下：

#ifndef _COMMON_H_
#define _COMMON_H_

#define max2(a, b) ((a) > (b) ? (a) : (b))
#define max3(a, b, c) max2(max2(a, b), c)
#define min2(a, b) ((a) < (b) ? (a) : (b))
#define show_func_result(func, a, b) printf("%s(%d, %d) = %d\n", #func, (a), (b), func((a), (b)))

#endif

2.2 求最大公约数

欧几里得算法求最大公约数，最坏情况下时间复杂度为O(NlogN)，实现如下：

/*
 * 求最大公约数，欧几里得算法
 * */
#include 
#include "common.h"

int get_gcd(int a, int b)
{
    int m = max2(a, b);
    int n = min2(a, b);
    int rem;

    do {
        rem = m % n;
        m = n;
        n = rem;
    } while (rem != 0);

    return m;
}

int main(void)
{
    show_func_result(get_gcd, 1989, 1590);
    show_func_result(get_gcd, 100, 20);
    show_func_result(get_gcd, 983, 23);

    return 0;
}

2.3 快速求幂算法

求幂算法中，如果求2^N = 2 * 2 * … * 2的方式计算，其中必定有很多重复运算，如果对2^N进行分解，可以避免很多重复运算，下面是递归和非递归的实现

/*
 * 快速求幂算法
 */
#include 
#include "common.h"

/* 递归算法 */
int mypow(int a, int n)
{
    if (n == 1) {
        return a;
    }

    if (n % 2 == 0) {
        return mypow(a * a, n / 2);
    } else {
        return mypow(a * a, n / 2) * a;
    }
}

/* 非递归算法 */
int mypow2(int a, int n)
{
    int i;
    int base = a;
    int ext = 1;

    for (i = n; i != 1; i /= 2) {
        if (i % 2 != 0) {
            ext *= base;
        }
        base *= base;
    }

    return base * ext;
}

int main(void)
{
    show_func_result(mypow2, 2, 10);     // 2^10 = 4^5 = 16^2 * 4 = 256 * 4
    show_func_result(mypow, 3, 7);      // pow(3, 7) = pow(9, 3) * 3 = pow(81, 1) * 9 * 3 = 81 * 9 * 3

    return 0;
}

总结

1. 思考算法中哪些部分的运算是重复的，如何才能做到减少这些重复运算。
2. 分治思想对与线性的问题可以有效的简化，思考那些情况可以采用分治思想。