平衡二叉树 AVL
平衡二叉树 AVL
先弄清楚几个概念:
1)满二叉树:除了叶子节点,都是满的;
2)完全二叉树:整体而言,空缺的节点一定是位于树的右下方;整棵树的叶子节点最大深度值和最小深度值,相差不会超过1;
3)平衡二叉树:对于任意一个节点,左子树和右子树的高度差不能超过1。

1 平衡因子
通过平衡因子可以判断出是否为平衡二叉树,这决定了是否需要进行左旋转或右旋转操作。
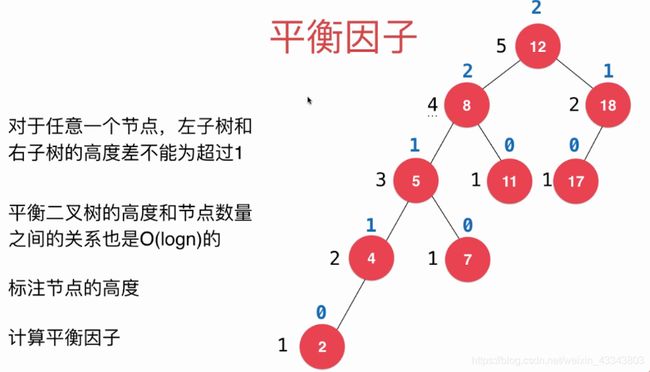
第一步,标注节点的高度;节点的高度=其左右子节点的最大高度值+1;叶子节点的高度为1。
第二步,平衡因子=左右子节点的高度之差。
从上图中可以看到8,、12节点,平衡因子>1,导致了不平衡。
标注节点高度和平衡因子的实现:
//返回高度值
int getHeight(AVLNode<K,V> *node){
if(node== nullptr)
return 0;
return node->height;//节点高度作为成员变量,初始值为1
}
//获得节点node的平衡因子
int getBalanceFactor(AVLNode<K,V> *node){
if(node==nullptr)
return 0;
return getHeight(node->left)-getHeight(node->right);//左右子树高度之差
}
判断一棵树的平衡性:
//判断是否是一颗平衡二叉树,自顶向下遍历,递归算法
bool isBalanced(AVLNode<K,V> *node){
if(node==nullptr)
return true;
int balanceFactor=getBalanceFactor(node);
if(std::abs(balanceFactor)>1)//平衡因子>1
return false;
return isBalanced(node->left)&&isBalanced(node->right);//左右子树同时满足
}
2 维护平衡操作
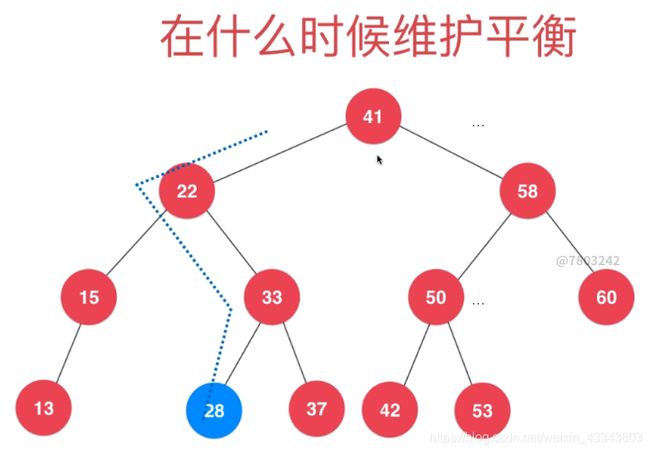
维护的时机:
二叉树添加一个元素,一定是插入到一个叶子节点。由于新添加了一个节点,才有可能导致树失去平衡性。相应地,这个不平衡的节点只有可能发生从插入的这个位置节点向父亲去找。
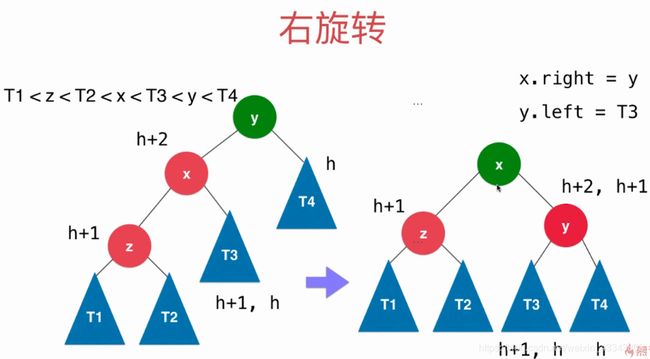
2.1 右旋转(以x为旋转点)
//右旋转
AVLNode<K,V> *rightRotate(AVLNode<K,V> *y){
AVLNode<K,V> *x=y->left;//x是谁?是y的左子树
AVLNode<K,V> *T3=x->right;//暂存T3,因为后面要把它接到y节点,作为左子树
//向右旋转
x->right=y;
y->left=T3;
//更新height,先更新y的高度值,因为x是基于y来计算的
y->height=std::max(getHeight(y->left),getHeight(y->right))+1;
x->height=std::max(getHeight(x->left),getHeight(x->right))+1;
return x;
}
2.2 左旋转(以x为旋转点) 
左旋转的实现:
AVLNode<K,V> *leftRotate(AVLNode<K,V> *y){
AVLNode<K,V> *x=y->right;
AVLNode<K,V> *T3=x->left;
//向左旋转
x->left=y;
y->right=T3;
//更新height
y->height=std::max(getHeight(y->left),getHeight(y->right))+1;
x->height=std::max(getHeight(x->left),getHeight(x->right))+1;
return x;
}
2.3 添加元素在不平衡节点的左侧的右侧
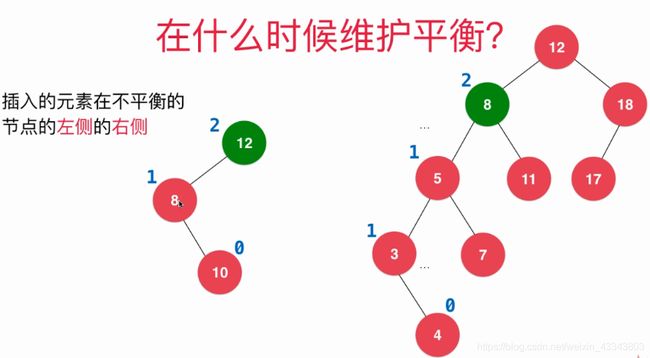
前面实现的左旋转和右旋转,如果新添加的节点位于不平衡节点的左侧的左侧,就是LL;如果新添加的节点位于不平衡节点的右侧的右侧,就是RR;

如果新添加的节点位于不平衡节点的左侧的右侧,就是LR;
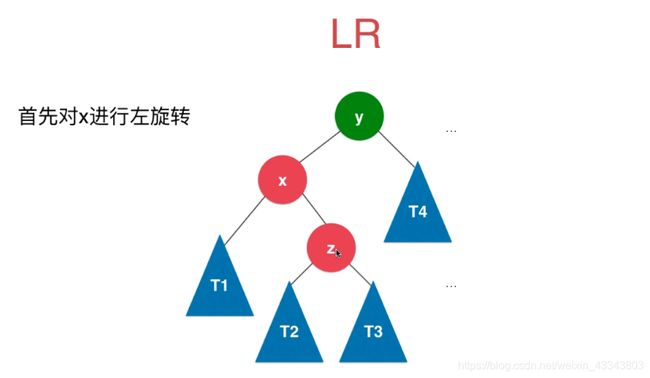
以x进行左旋转;
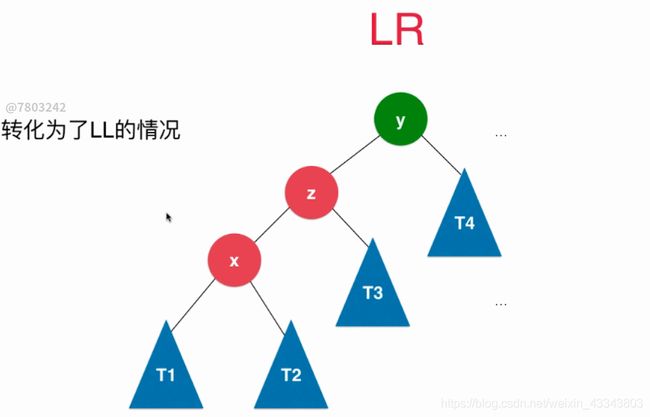
如果新添加的节点位于不平衡节点的右侧的左侧,就是RL;
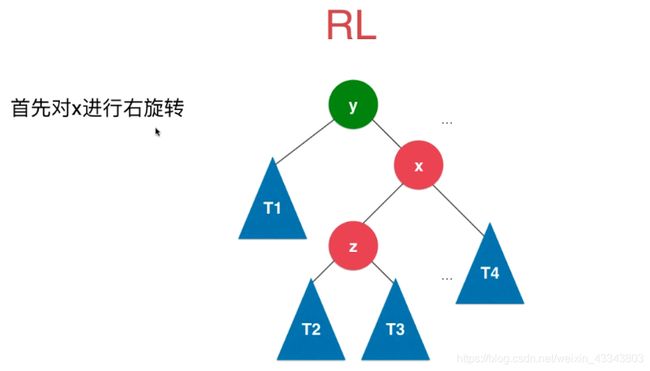
以x进行右旋转;

平衡性维护实现:
if(balanceFactor>1 && getBalanceFactor(node->left)>=0)
return rightRotate(node);
//RR
if(balanceFactor<-1 && getBalanceFactor(node->right)<=0)
return leftRotate(node);
//LR
if(balanceFactor>1 && getBalanceFactor(node->left)<0){
node->left=leftRotate(node->left);
return rightRotate(node);
}
//RL
if(balanceFactor<-1 && getBalanceFactor(node->right)>0){
node->right=rightRotate(node->right);
return leftRotate(node);
}
AVL添加操作实现:
AVLNode<K,V> *add(AVLNode<K,V> *node,K key,V value){
if(node== nullptr){
size++;
return new AVLNode<K,V>(key,value);
}
if(key==node->key){
node->value=value;
} else if(key<node->key){
node->left=add(node->left,key,value);
}else {
node->right=add(node->right,key,value);
}
//更新height
node->height=1+std::max(getHeight(node->left),getHeight(node->right));
//计算平衡因子
int balanceFactor =getBalanceFactor(node);
//平衡维护
//LL
if(balanceFactor>1 && getBalanceFactor(node->left)>=0)
return rightRotate(node);
//RR
if(balanceFactor<-1 && getBalanceFactor(node->right)<=0)
return leftRotate(node);
//LR
if(balanceFactor>1 && getBalanceFactor(node->left)<0){
node->left=leftRotate(node->left);
return rightRotate(node);
}
//RL
if(balanceFactor<-1 && getBalanceFactor(node->right)>0){
node->right=rightRotate(node->right);
return leftRotate(node);
}
return node;
}
AVL删除操作实现:
// 删除掉以node为根的二分搜索树中键值为key的节点
// 返回删除节点后新的二分搜索树的根
AVLNode<K,V> *remove(AVLNode<K,V> *node, K key) {
if (node == nullptr) {
return nullptr;
}
AVLNode<K,V> *retNode=nullptr;
if (key < node->key) {
node->left = remove(node->left, key);
retNode=node;
} else if (key > node->key) {
node->right = remove(node->right, key);
retNode= node;
} else {
if (node->left == nullptr) {
AVLNode<K,V> *rightNode = node->right;
delete node;
size--;
retNode= rightNode;
}
else if (node->right == nullptr) {
AVLNode<K,V> *leftNode = node->left;
delete node;
size--;
retNode= leftNode;
}
else{
AVLNode<K,V> *successor = new AVLNode<K,V>(minimum(node->right));
//Node *precursor = new Node(maximum(node->right));
size++;
successor->right = remove(node->right,successor->key);
successor->left = node->left;
//precursor->left = removeMax(node->left);
//precursor->right = node->right;
delete node;
size--;
retNode= successor;
//return precursor;
}
}
if(retNode== nullptr)
return nullptr;
//更新height
retNode->height=1+std::max(getHeight(retNode->left),getHeight(retNode->right));
//计算平衡因子
int balanceFactor =getBalanceFactor(retNode);
//平衡维护
//LL
if(balanceFactor>1 && getBalanceFactor(retNode->left)>=0)
return rightRotate(retNode);
//RR
if(balanceFactor<-1 && getBalanceFactor(retNode->right)<=0)
return leftRotate(retNode);
//LR
if(balanceFactor>1 && getBalanceFactor(retNode->left)<0){
retNode->left=leftRotate(retNode->left);
return rightRotate(retNode);
}
//RL
if(balanceFactor<-1 && getBalanceFactor(retNode->right)>0){
retNode->right=rightRotate(retNode->right);
return leftRotate(retNode);
}
return retNode;
}