【图论】中国邮递员问题、平面图上最大割问题的多项式时间算法
文章目录
- 一、中国邮递员问题
-
- 1. 与欧拉回路的关系
- 2. Edmonds-Johnson算法
- 3. 一个例子
- 二、平面图上的最大割问题
-
- 1. 割
- 2. 最大割及其 N P \bold{NP} NP完全性
- 3. 平面图上的最大割问题
- 4. 奇回路覆盖
- 5. 转化为一般图最大匹配
- 6. 一个例子
- 三、顶点图上最大割问题的 N P \bold{NP} NP完全性
- 参考资料
一、中国邮递员问题
中国邮递员问题(Chinese Postman Problem, CPP)是图论中的一个著名问题,它是在1960年由我国学者管梅谷首先提出并研究的。简单来说,就是问:一个邮递员从邮局出发,把一个城市的所有街道都至少走一遍,最后回到邮局,问怎样使他走的总路程最小?这个问题有许多现实的应用,比如一个除雪车从城市的某一位置出发,把城市里所有街道的雪都清扫了,再回到出发点,问怎么走路程最少。我们可以把城市看作一个连通的、简单的带权无向图,节点代表街道的交叉,边代表街道,其权重是街道的长度。一个回路(circuit)是从某一点出发回到这一点的路径,并且可以将一条边经过多次。所以,中国邮递员问题就是求无向图上权重最小(即最短)的回路。
1. 与欧拉回路的关系
说到回路,我们肯定会想起欧拉回路(Eulerian circuit),它是在一个无向图中能够访问所有边恰好一次的回路(即“一笔画”)。显然,一个图如果含有欧拉回路,那欧拉回路就是邮递员的最佳路径了(因为他只用把每条边访问一次)。一个连通图有欧拉回路当且仅当所有节点的度数都为偶数。如果这个条件不满足,那么图中就没有欧拉回路,这时邮递员就必须把某些边访问两次及以上。也就是说,我们要在图中找到一些边,把它们复制,使得得到的多重图有欧拉回路,并且这些被复制的边的权重之和最小。
2. Edmonds-Johnson算法
管梅谷解决这个问题的方法是“奇偶点图上作业法”,但是复杂度太高,我们这里介绍复杂度更优的Edmonds-Johnson算法。首先,会“坏事儿”的节点就是图上具有奇度数的节点(称为奇节点,度数为偶数的叫偶节点),我们必须给每个奇节点复制一条(从它开始的)边。当图上所有节点都是偶节点时,才有欧拉回路。其次,我们可以看出,每条边至多被复制一次(也就是被邮递员经过两次),因为如果复制两次及以上,邮递员相当于要从这头走到那头又回来,白走了很多路程。或者说,至多复制一次就可以让一个奇节点变成偶节点,所以没必要复制更多次。
我们还可以观察到,一个无向图中奇节点的个数一定是偶数。为什么呢?握手引理(Handshaking Lemma)说的是:无向图中所有节点的度数之和等于边数乘2,那么度数之和和一定是偶数。而只有偶数个奇数之和才能是偶数,所以奇节点一定有偶数个。好了,现在我们假设图中有 2 m 2m 2m个奇节点,它们组成的集合为 S = { v 1 , v 2 , ⋯ , v 2 m } S=\{v_1,v_2,\cdots,v_{2m}\} S={v1,v2,⋯,v2m}。我们考虑把 v 1 v_1 v1变成偶节点,那么需要把一条从 v 1 v_1 v1出发的边复制一份。假设这条边为 ( v 1 , u ) (v_1,u) (v1,u), u u u本来是偶节点,把它复制一份, v 1 v_1 v1确实变成了偶节点,但 u u u又变成奇节点了。接着又得把 u u u再变成偶节点,假设我们把 ( u , h ) (u,h) (u,h)复制一份, u u u变偶, h h h变奇,再把 ( h , l ) (h,l) (h,l)复制一份, h h h变偶, l l l变奇,……什么时候才能结束呢?直到遇到另一个 S S S中的节点 v x v_x vx(即本来度数为奇数的节点),使得 v x v_x vx从奇变偶了,才能结束。(如果 v 1 v_1 v1本来就和某个奇节点 v x v_x vx相邻,那么只需要把 ( v 1 , v x ) (v_1,v_x) (v1,vx)复制一份即可。)其实我们发现,我们把 v 1 v_1 v1到 v x v_x vx的路径都复制了一份,使得 v 1 v_1 v1、 v x v_x vx的度数+1,中间节点的度数+2,那么这条路径上的所有节点都变成偶节点了。注意,我们想要增加的边的权重之和最小,那我们复制的一定是从 v 1 v_1 v1到 v x v_x vx的最短路,而不是其他更长的路径。 v 1 ( 奇 ) ⟶ u ⟶ h ⟶ l ⟶ ⋯ ⟶ v x ( 奇 ) v_1(\text{奇})\longrightarrow u\longrightarrow h\longrightarrow l\longrightarrow\cdots\longrightarrow v_x(\text{奇}) v1(奇)⟶u⟶h⟶l⟶⋯⟶vx(奇)好了,我们现在知道,把两个奇节点 v i v_i vi和 v j v_j vj之间的路径复制一份,可以把 v i v_i vi和 v j v_j vj都变成偶节点,花费的代价是 v i v_i vi和 v j v_j vj之间的最短距离(即最短路长度)。我们定义:如果把 v i v_i vi到 v j v_j vj的最短路径复制了一份,则称 v i v_i vi和 v j v_j vj配对。一个奇节点只能和另外的一个奇节点配对,因为如果和两个奇节点配对的话,那它的度数加2,它还是奇节点。(如果和三个奇节点配对,设这三个奇节点为 v x , v y , v z v_x,v_y,v_z vx,vy,vz,那么可以视为它和 v x v_x vx配对, v y v_y vy通过它和 v z v_z vz配对。以此类推。)于是,这个问题就变成了一个最小权匹配问题。至此,Edmonds-Johnson算法也就逐渐浮出水面了。
Edmonds-Johnson算法的步骤是:
- 对于连通的无向简单图 G = ( V , E ) G=(V,E) G=(V,E)(邮局在哪里其实没有关系),设 S = { v 1 , v 2 , ⋯ , v 2 m } S=\{v_1,v_2,\cdots,v_{2m}\} S={v1,v2,⋯,v2m}是其中度数为奇数的节点。对于 S S S中任意的节点对 ( v i , v j ) (v_i,v_j) (vi,vj),计算它们的最短路径长度 l i j l_{ij} lij。这一步可以由Floyd全源最短路算法完成。
- 建立一个带权无向完全图 K 2 m K_{2m} K2m,其节点集是 S S S,每对节点 v i , v j v_i,v_j vi,vj之间都有边,边权是 G G G中 v i , v j v_i,v_j vi,vj的最短路径 l i j l_{ij} lij。接着,我们需要找到 K 2 m K_{2m} K2m的最小权完美匹配 M M M, M M M是由 m m m条边组成的集合,其中任两条边之间没有公共端点。(“完美”匹配指的是每个奇节点都有与之配对的节点。)寻找最小权完美匹配的过程可以由Edmonds算法在 O ( n 3 ) O(n^3) O(n3)的时间内完成( n n n为 G G G中节点个数)。
- 在 G G G中,把 M M M内每条边对应的路径复制一份,得到多重图 G ′ G' G′。
- 求出 G ′ G' G′的欧拉回路(可以采用Fleury算法),这就是邮递员的最优路径。最终,邮递员所要走的路程是 G G G中边权之和(记为 w ( G ) w(G) w(G))+ M M M中边权之和(记为 w ( M ) w(M) w(M))。
因为Floyd全源最短路算法的复杂度为 O ( n 3 ) O(n^3) O(n3),求 K 2 m K_{2m} K2m最小权完美匹配的复杂度为 O ( n 3 ) O(n^3) O(n3),所以Edmonds-Johnson算法总的复杂度为 O ( n 3 ) O(n^3) O(n3)。
3. 一个例子
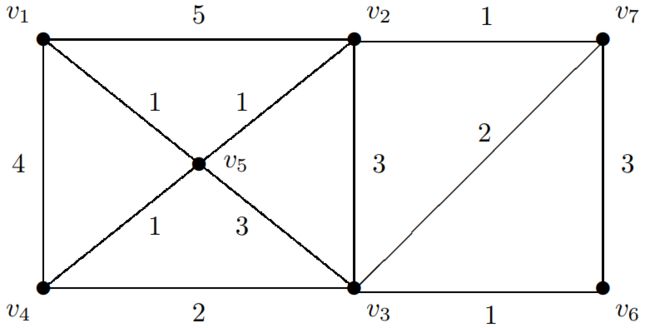
假设城市的地图如下:
可以看到,奇节点组成的集合 S = { v 1 , v 3 , v 4 , v 7 } S=\{v_1,v_3,v_4,v_7\} S={v1,v3,v4,v7},它们的度数分别为 3 , 5 , 3 , 3 3,5,3,3 3,5,3,3。 m = 2 m=2 m=2。
它们之间的最短路径及最短距离如下:
- P 13 = v 1 → v 5 → v 3 P_{13}=v_1\to v_5\to v_3 P13=v1→v5→v3, l 13 = 4 l_{13}=4 l13=4
- P 14 = v 1 → v 5 → v 4 P_{14}=v_1\to v_5\to v_4 P14=v1→v5→v4, l 14 = 2 l_{14}=2 l14=2
- P 17 = v 1 → v 5 → v 2 → v 7 P_{17}=v_1\to v_5\to v_2\to v_7 P17=v1→v5→v2→v7, l 17 = 3 l_{17}=3 l17=3
- P 34 = v 3 → v 4 P_{34}=v_3\to v_4 P34=v3→v4, l 34 = 2 l_{34}=2 l34=2
- P 37 = v 3 → v 7 P_{37}=v_3\to v_7 P37=v3→v7, l 37 = 2 l_{37}=2 l37=2
- P 47 = v 4 → v 5 → v 2 → v 7 P_{47}=v_4\to v_5\to v_2\to v_7 P47=v4→v5→v2→v7, l 47 = 3 l_{47}=3 l47=3
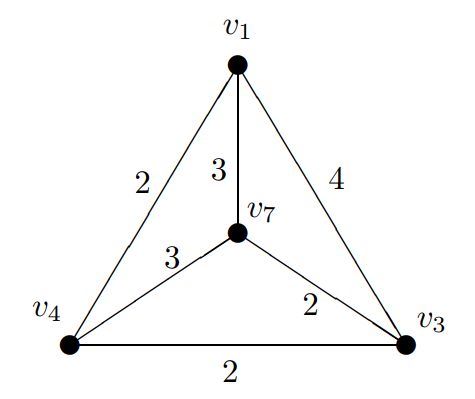
据此构造完全图 K 2 m K_{2m} K2m:
求出其最小权完美匹配 M = { ( v 1 , v 4 ) , ( v 3 , v 7 ) } M=\{(v_1,v_4),(v_3,v_7)\} M={(v1,v4),(v3,v7)}:
也就是说,对于 v 1 v_1 v1与 v 4 v_4 v4之间的最短路径( v 1 → v 5 → v 4 v_1\to v_5\to v_4 v1→v5→v4)、 v 3 v_3 v3与 v 7 v_7 v7之间的最短路径( v 3 → v 7 v_3\to v_7 v3→v7),邮递员要走两次。将这些路径复制后得到的多重图 G ′ G' G′如下:
最后,我们构建 G ′ G' G′的一个欧拉回路: R = v 1 → v 2 → v 3 → v 4 → v 1 → v 5 → v 2 → v 7 → v 3 → v 7 → v 6 → v 3 → v 5 → v 4 → v 5 → v 1 R=v_1\to v_2\to v_3\to v_4\to v_1\to v_5\to v_2\to v_7\to v_3\to v_7\to v_6\to v_3\to v_5\to v_4\to v_5\to v_1 R=v1→v2→v3→v4→v1→v5→v2→v7→v3→v7→v6→v3→v5→v4→v5→v1,其权重为 w ( G ) + w ( M ) = 27 + 4 = 31 w(G)+w(M)=27+4=31 w(G)+w(M)=27+4=31。
二、平面图上的最大割问题
1. 割
给定无向图 G = ( V , E ) G=(V,E) G=(V,E),现在把点集 V V V分成两个集合 S , T S,T S,T使得 S ∪ T = V S\cup T=V S∪T=V且 S ∩ T = ∅ S\cap T=\emptyset S∩T=∅,这样的一种分割方式 G G G的一个割(cut),边集 C = { ( u , v ) ∣ u ∈ S , v ∈ T } C=\{(u,v)|u\in S,v\in T\} C={(u,v)∣u∈S,v∈T}称为由该割决定的割集(cut set),把割集从 G G G中删除后 S S S和 T T T两部分就不连通了。割集中的每条边都是横跨 S S S和 T T T两个集合的。
2. 最大割及其 N P \bold{NP} NP完全性
G G G的最大割(maximum cut)是使得割集中含有边数最多的割,也就是使 S S S和 T T T内部的边最少的割。求一般图的最大割是 N P \bold{NP} NP难问题(对应的判定问题,即判断一个图 G G G中是否有边数至少为 k k k的割是 N P \bold{NP} NP完全问题)。接下来我们通过将最大独立集(maximum independent set, MIS)归约到最大割。
给定图 G = ( V , E ) G=(V,E) G=(V,E),我们要求它的最大独立集。下面我们说明,如果我们判定了另一个图 G ′ = ( V ′ , E ′ ) G'=(V',E') G′=(V′,E′)的最大割问题,就可以判定 G G G的最大独立集问题。把 G G G变成 G ′ G' G′的过程如下:在 G G G中新添加一个节点 x x x(可理解为“超级源点”),并让它与 V V V中所有节点相连(即 ∀ u ∈ V \forall u\in V ∀u∈V,添加边 ( x , u ) (x,u) (x,u))。接下来,对于 E E E中的每条边 e = ( u , v ) e=(u,v) e=(u,v),添加两个节点 u e , v e u_e,v_e ue,ve,并向 E ′ E' E′中添加五条边 ( u , u e ) , ( v , v e ) , ( x , u e ) , ( x , v e ) , ( u e , v e ) (u,u_e),(v,v_e),(x,u_e),(x,v_e),(u_e,v_e) (u,ue),(v,ve),(x,ue),(x,ve),(ue,ve)(注意 E ′ E' E′并不含有 E E E中的边)。我们令 G e = ( { u , v , u e , v e , x } , { ( u , u e ) , ( v , v e ) , ( x , u e ) , ( x , v e ) , ( u e , v e } ) G_e=(\{u,v,u_e,v_e,x\},\{(u,u_e),(v,v_e),(x,u_e),(x,v_e),(u_e,v_e\}) Ge=({u,v,ue,ve,x},{(u,ue),(v,ve),(x,ue),(x,ve),(ue,ve})为边 e e e对应的附件图(gadget),它就是下图中标粗的部分:
现在, ∣ V ′ ∣ = ∣ V ∣ + 1 + 2 ∣ E ∣ |V'|=|V|+1+2|E| ∣V′∣=∣V∣+1+2∣E∣, ∣ E ′ ∣ = ∣ E ∣ + ∣ V ∣ + 5 ∣ E ∣ = 6 ∣ E ∣ + ∣ V ∣ |E'|=|E|+|V|+5|E|=6|E|+|V| ∣E′∣=∣E∣+∣V∣+5∣E∣=6∣E∣+∣V∣。我们接下来证明: G G G包含一个大小至少为 k k k的独立集 I ⟺ G ′ I\iff G' I⟺G′中存在一种分割 V ′ V' V′的方法: V ′ = S ∪ T V'=S\cup T V′=S∪T,使得割集 C C C的大小 ∣ C ∣ ≥ k + 4 ∣ E ∣ |C|\ge k+4|E| ∣C∣≥k+4∣E∣。
⟹ \implies ⟹:对于给定的独立集 I I I,我们构造一个点集 S S S。一开始 S = I S=I S=I。然后对于 E E E中的每条边 e = ( u , v ) e=(u,v) e=(u,v),做以下几件事:
- 若 u ∈ I u\in I u∈I且 v ∉ I v\notin I v∈/I,则将 v e v_e ve加入 S S S。相似地,若 v ∈ I v\in I v∈I且 u ∉ I u\notin I u∈/I,则将 u e u_e ue加入 S S S。此时,在 e e e对应的附件图 G e G_e Ge中,有两个节点属于 S S S,三个节点不属于 S S S,五条边中有四条边(除了 x x x与 u u u或 v v v相连的那条)都是割边。
- 若 u , v ∉ I u,v\notin I u,v∈/I,则将 u e u_e ue和 v e v_e ve都加入 S S S。这下 G e G_e Ge中仍然有四条边是割边(除了 ( u e , v e ) (u_e,v_e) (ue,ve)不是)。
注意 u , v u,v u,v不可能都属于 I I I,因为 I I I是一个独立集。此外, x x x不在 S S S中,因此 I I I中节点与 x x x相连的边都是割边。每个附件图 G e G_e Ge中都有四条边为割边,因此 ∣ C ∣ = ∣ I ∣ + 4 ∣ E ∣ = k + 4 ∣ E ∣ |C|=|I|+4|E|=k+4|E| ∣C∣=∣I∣+4∣E∣=k+4∣E∣。
⟸ \Longleftarrow ⟸:现在我们有一个大小至少为 k + 4 ∣ E ∣ k+4|E| k+4∣E∣的割集 C C C,它把 V ′ V' V′分割成 S S S和 T T T,接下来要构造一个独立集 I I I使得 ∣ I ∣ ≥ k |I|\ge k ∣I∣≥k。首先,我们假设 x ∈ S x\in S x∈S,因为如果 x ∉ S x\notin S x∈/S,我们把 S S S和 T T T互换即可。其次,我们找到 S S S中属于 V V V的节点,组成集合 I I I。对于 E E E中的任意边 e = ( u , v ) e=(u,v) e=(u,v),若 u , v ∈ S u,v\in S u,v∈S,则 G e G_e Ge中至多有三条割边;若 u u u和 v v v至少有一个不属于 S S S,则 G e G_e Ge中至多有四条割边。设第一种情况发生的次数为 m ( I ) m(I) m(I),或者说 m ( I ) = ∣ { ( u , v ) ∈ E ∣ u , v ∈ I } ∣ m(I)=\left|\{(u,v)\in E|u,v\in I\}\right| m(I)=∣{(u,v)∈E∣u,v∈I}∣(即 I I I内部的边),那么第二种情况发生的次数为 ∣ E ∣ − m ( I ) |E|-m(I) ∣E∣−m(I)。所以,割边的个数满足 ∣ C ∣ ≤ ∣ I ∣ ↑ 从 x 出发的边 + 3 ⋅ m ( I ) ↑ 第一种情况 + 4 ⋅ [ ∣ E ∣ − m ( I ) ] ↑ 第二种情况 = ∣ I ∣ + 4 ∣ E ∣ − m ( I ) |C|\le\underset{\underset{\text{从}x\text{出发的边}}{\uparrow}}{|I|}+\underset{\underset{第一种情况}{\uparrow}}{3\cdot m(I)}+\underset{\underset{第二种情况}{\uparrow}}{4\cdot[|E|-m(I)]}=|I|+4|E|-m(I) ∣C∣≤从x出发的边↑∣I∣+第一种情况↑3⋅m(I)+第二种情况↑4⋅[∣E∣−m(I)]=∣I∣+4∣E∣−m(I)即 ∣ I ∣ ≥ m ( I ) − 4 ∣ E ∣ + ∣ C ∣ |I|\ge m(I)-4|E|+|C| ∣I∣≥m(I)−4∣E∣+∣C∣;由 ∣ C ∣ ≥ k + 4 ∣ E ∣ |C|\ge k+4|E| ∣C∣≥k+4∣E∣得 ∣ I ∣ ≥ m ( I ) + k |I|\ge m(I)+k ∣I∣≥m(I)+k。现在 I I I可能还不是独立集,因为 I I I内部还有边。不过, I I I内部的边只有 m ( I ) m(I) m(I)条,现在我们从 I I I中移除一些节点,如果 ( u , v ) ∈ E (u,v)\in E (u,v)∈E且 u , v ∈ I u,v\in I u,v∈I,那么我们移除 u u u,则 I I I内部的边至少减少 1 1 1条,所以我们至多移除 m ( I ) m(I) m(I)个节点就可以使 I I I变为独立集了,此时 ∣ I ∣ ≥ k |I|\ge k ∣I∣≥k。至此,我们就将最大独立集问题归约到了最大割。
虽然最大割是 N P \bold{NP} NP难的,最小割却可以在多项式时间内求解。根据最大流最小割定理,求最小割相当于求任两个节点间最大流的最大值,这可以用Ford-Fulkson方法或Dinic算法求解。
3. 平面图上的最大割问题
一个 N P \bold{NP} NP完全问题的某些特殊情况可以在多项式时间内求解。作为一个例子,最大割问题在平面图(planar graph)上就可以在多项式时间内求解。本文介绍的算法是F. Hadlock首先提出的(论文:Hadlock, F.O. (1975). Finding a Maximum Cut of a Planar Graph in Polynomial Time. SIAM J. Comput., 4, 221-225.)。
首先,我们最希望的情况就是图 G G G是二分图(bipartite graph)。如果 G G G是二分图,那么其节点集可以被分为两个集合 S ∪ T S\cup T S∪T,使得每条边都横跨 S S S和 T T T。此时,每条边都是割边,最大割的大小就是边数。一个图是二分图当且仅当它没有奇圈。平面图的一个平面嵌入可以被分成很多面,每个面被一个圈包围,圈的长度(边数)称为这个面的次数。如果所有面的次数都为偶数,那么这个平面图是二分图,就万事大吉了;但如果这个面的次数是奇数,那就会出现问题——肯定有边不是割边。因此,我们要处理的“刺头”就是奇回路(如果一个面的次数为奇数,则其边界为奇圈,奇回路中一定有奇圈)。
4. 奇回路覆盖
由于奇回路会坏事儿,我们希望移除一些边使得剩下的图是二分图(即不含有奇回路)。并且,我们希望移除的边越少越好,因为剩下的边一定是割边。如果移除边集 D D D可以使图 G G G变成二分图(即不含寄回路),则称 D D D是奇回路覆盖(odd-circuit cover)。我们的目标就是求最小奇回路覆盖(minimum odd-circuit cover),即含有边最少的奇回路覆盖。
5. 转化为一般图最大匹配
我们将会看到,处理平面图上最大割问题的方式与处理中国邮递员问题的方式有异曲同工之妙。如果一个面的次数为奇数,我们称这个面为奇面(相应地有偶面)。一条边是同时充当两个面的边界的,所以面的次数之和等于边数的两倍,也就是说面的次数之和为偶数,因此奇面一定有偶数个。对于奇面 A A A,我们需要移除其一条边,使奇回路被破坏。而这条边同时也是另一个面(设为 B B B)的边界,所以移除这条边之后面 B B B也少了一条边,那这两个面就被打通了,形成了一个新的大面。
如果 B B B是偶面,如上图所示,则形成的大面 B ′ B' B′是奇面(注意蓝色的边要算两次),这意味着它还有奇回路。那么就把 B ′ B' B′的一条边删除,使它和另一个偶面 C C C打通,形成更大的奇面 C ′ C' C′。……如此循环往复,直到大面可以和某个本来就是奇面的面 Z Z Z打通,而奇面和奇面打通形成的面是偶面,这样我们就消除了原图中奇面 A A A和奇面 Z Z Z中的奇圈。我们可以理解为,面 A A A和 Z Z Z配对,为了打通 A A A和 Z Z Z,需要把沿路的偶面 B B B、 C C C、……、 Y Y Y也打通。
当然,把两个面打通需要删除一条边,我们需要让删除的边数最少。因此,我们需要找到面 A A A和面 Z Z Z的“最短路径”。如果我们把每个面看成一个顶点,那么处理起来会十分方便。正好,对偶图(dual graph)可以帮助到我们。
对于一个平面图 G G G,其对偶图 G ∗ G^* G∗可能是一个多重图(含有自环和重边),每个节点对应 G G G中的一个面,如果 G G G中两个面被一条边分开则对偶图中两个面所对应的两个顶点有一条横跨该边的边。可以看到,如果 G G G中有奇面 A A A,则 A A A在对偶图中对应的节点 a a a就是奇节点。在 G G G中将面 A , B A,B A,B打通,相当于在 G ∗ G^* G∗中移除 a , b a,b a,b之间的一条边。将 G G G中的面 A A A变成偶面,就是把 G ∗ G^* G∗中的点 a a a变为偶节点。是不是和中国邮递员问题很像了?只不过,我们把节点变成偶节点的方式是删边,而不是复制边。尽管如此,我们的目标是相似的:被删/复制的边的权重之和最小(这里每条边的权重都是 1 1 1,因此就是令被删的边数最少)。办法我们已经介绍过了:找出 G ∗ G^* G∗中的所有奇节点,构造以他们为节点的完全图,边 ( v i , v j ) (v_i,v_j) (vi,vj)的权重是 v i v_i vi和 v j v_j vj在 G ∗ G^* G∗中的最短距离,然后找出完全图的最小权完美匹配。如果 v i v_i vi和 v j v_j vj匹配,那就是从 v i v_i vi对应的面出发,一路删边到 v j v_j vj对应的面,且保证经过的面最少。(最后 v i v_i vi对应的面和 v j v_j vj对应的面以及路上经过的所有面都被打通成一个面了。)在对每个奇节点对进行删边操作后,剩下的图就是二分图,其中的每条边都是割边,我们也就求得了最大割中割边的个数。
6. 一个例子
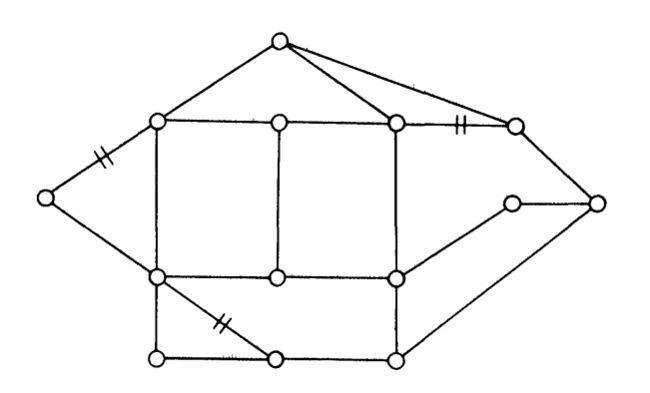
考虑下列平面图 G G G:
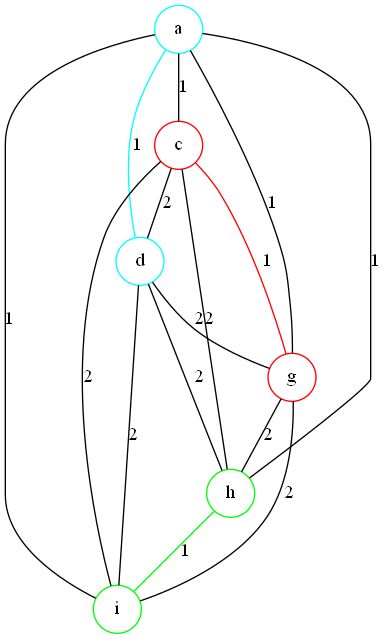
其对偶图 G ∗ G^* G∗为:
其中标红的节点为奇节点( S = { a , c , d , g , h , i } S=\{a,c,d,g,h,i\} S={a,c,d,g,h,i})。
在求得 S S S中节点两两之间的最短路径后,我们构造完全图 K 6 K_{6} K6:
求得其最小权完美匹配 M = { ( a , d ) , ( c , g ) , ( h , i ) } M=\{(a,d),(c,g),(h,i)\} M={(a,d),(c,g),(h,i)},并删掉对应的边:
删掉的边就是 G G G的最小奇回路覆盖。剩下的是一个二分图,有 18 18 18条边,因此 G G G的最大割的边数为 18 18 18。
三、顶点图上最大割问题的 N P \bold{NP} NP完全性
顶点图(apex graph)指的是移除一个节点就可以把它变成平面图的图。移除的那个节点叫做顶点(apex)。一个顶点图可以有多个顶点,如 K 5 K_5 K5的所有点都是顶点,因为不论移除那个节点最后剩下的图都是平面图 K 4 K_4 K4。我们将要证明,虽然最大割在平面图上可以在多项式时间内求解,但是只多了一个节点——顶点,问题就变成 N P \bold{NP} NP完全的了。
首先,平面图上的最大独立集问题是 N P \bold{NP} NP完全的,证明见Mohar, B. (2001). Face Covers and the Genus Problem for Apex Graphs. J. Comb. Theory, Ser. B, 82, 102-117.(方法是把平面3-SAT归约到平面图上的独立集问题)。然后,我们把平面图上的独立集归约到顶点图上的最大割问题。回顾“二、2”节的方法,假设 G G G是平面图,现在构造顶点图 G ′ G' G′。我们先不加入节点 x x x,只是为每条边 e = ( u , v ) ∈ E e=(u,v)\in E e=(u,v)∈E添加节点 u e , v e u_e,v_e ue,ve,那也就相当于把边 u − v u-v u−v换成了链 u − u e − v e − v u-u_e-v_e-v u−ue−ve−v,如果我们把 u e u_e ue和 v e v_e ve放在边 u − v u-v u−v的连线上,那得到的图仍然是平面图。现在加入节点 x x x,它与目前图中的每个节点都相连。加入 x x x后, G ′ G' G′就不一定是平面图了,但从 G ′ G' G′中移除 x x x后剩下的图是平面图。因此 x x x是 G ′ G' G′的一个顶点, G ′ G' G′是顶点图。这样我们就证明了顶点图上的最大割问题是 N P \bold{NP} NP完全的。
参考资料
- https://handwiki.org/wiki/Route_inspection_problem
- https://zhuanlan.zhihu.com/p/401982790
- http://web.eecs.umich.edu/~pettie/matching/Edmonds-Johnson-chinese-postman.pdf
- https://webspace.maths.qmul.ac.uk/b.jackson/MAS210/ch8.pdf
- https://www.math.uwaterloo.ca/~bico/papers/match_ijoc.pdf
- https://courses.cs.duke.edu/fall19/compsci638/fall19_notes/lecture22.pdf
- https://dx.doi.org/10.1137%2F0204019
- https://users.fmf.uni-lj.si/mohar/Papers/ApexGenus.pdf