第十一届蓝桥杯大赛软件类省赛C++研究生组
题目
- A 约数个数(5分,√)
- B 寻找2020(5分,√)
- C 平面分割(10分)
- D 蛇形填数(10分,√)
- E 七段码(15分)
- F 成绩分析(15分,√)
- G 回文日期(20分,√)
- H 作物杂交(20分,√)
- I 子串分值和(25分)
- J 荒岛探测(25分)
写在前面:题目是全的,但是由于能力问题,有些题目没做,每道题的分值和完成情况已在题目后面注明
A 约数个数(5分,√)
题目描述
本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。
1200000有多少个约数(只计算正约数)。
#include B 寻找2020(5分,√)
题目链接(输入的数量太大)
https://www.lanqiao.cn/problems/1065/learning/
横向、纵向、对角线方向分别判断相连的四个字符是否是2020即可。
#define _CRT_SECURE_NO_WARNINGS
#include C 平面分割(10分)
题目描述
本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。
20 个圆和 20 条直线最多能把平面分成多少个部分?
D 蛇形填数(10分,√)
本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。
如下图所示,小明用从 11 开始的正整数“蛇形”填充无限大的矩阵。
1 2 6 7 15 …
3 5 8 14 …
4 9 13 …
10 12 …
11 …
…
容易看出矩阵第二行第二列中的数是 55。请你计算矩阵中第 2020 行第 2020 列的数是多少?
找规律。对角线为1,5,13,25,41……。两个数相差分别为4,8,12,16,……
#define _CRT_SECURE_NO_WARNINGS
#include E 七段码(15分)
方法比较笨,直接暴力。遍历每根管,以某根管为开始和其他所有管看是否相连,每次加入一根管就将该序列加入set中,保存结果。
#define _CRT_SECURE_NO_WARNINGS
#include F 成绩分析(15分,√)
题目描述
小蓝给学生们组织了一场考试,卷面总分为 100 分,每个学生的得分都是一个 0 到 100 的整数。
请计算这次考试的最高分、最低分和平均分。
输入描述
输入的第一行包含一个整数 (1 ≤ n ≤ 104),表示考试人数。
接下来 n 行,每行包含一个 0 至 100 的整数,表示一个学生的得分。
输出描述
输出三行。
第一行包含一个整数,表示最高分。
第二行包含一个整数,表示最低分。
第三行包含一个实数,四舍五入保留正好两位小数,表示平均分。
输入输出样例
输入
7
80
92
56
74
88
99
10
输出
99
10
71.29
#define _CRT_SECURE_NO_WARNINGS
#include G 回文日期(20分,√)
题目描述
2020 年春节期间,有一个特殊的日期引起了大家的注意:2020 年 2 月 2 日。因为如果将这个日期按 “yyyymmdd” 的格式写成一个 8 位数是 20200202,恰好是一个回文数。我们称这样的日期是回文日期。
有人表示 20200202 是 “千年一遇” 的特殊日子。对此小明很不认同,因为不到 2 年之后就是下一个回文日期:20211202 即 2021 年 12 月 2 日。
也有人表示 20200202 并不仅仅是一个回文日期,还是一个 ABABBABA 型的回文日期。对此小明也不认同,因为大约 100 年后就能遇到下一个 ABABBABA 型的回文日期:21211212 即 2121 年 12 月 12 日。算不上 “千年一遇”,顶多算 “千年两遇”。
给定一个 8 位数的日期,请你计算该日期之后下一个回文日期和下一个 ABABBABA 型的回文日期各是哪一天。
输入描述
输入包含一个八位整数 NN,表示日期。
对于所有评测用例,10000101≤N≤89991231,保证 N 是一个合法日期的 8 位数表示。
输出描述
输出两行,每行 1 个八位数。第一行表示下一个回文日期,第二行表示下一个 ABABBABA 型的回文日期。
输入输出样例
输入
20200202
输出:
20211202
21211212
#define _CRT_SECURE_NO_WARNINGS
#include H 作物杂交(20分,√)
题目描述
作物杂交是作物栽培中重要的一步。已知有 N 种作物 (编号 1 至 N ),第 i 种作物从播种到成熟的时间为Ti 。作物之间两两可以进行杂交,杂交时间取两种中时间较长的一方。如作物 A 种植时间为 5 天,作物 B 种植时间为 7 天,则 AB 杂交花费的时间为 7 天。作物杂交会产生固定的作物,新产生的作物仍然属于 N 种作物中的一种。
初始时,拥有其中 M 种作物的种子 (数量无限,可以支持多次杂交)。同时可以进行多个杂交过程。求问对于给定的目标种子,最少需要多少天能够得到。
如存在 4 种作物 ABCD,各自的成熟时间为 5 天、7 天、3 天、8 天。初始拥有 AB 两种作物的种子,目标种子为 D,已知杂交情况为 A × B → C,A × C → D。则最短的杂交过程为:
第 1 天到第 7 天 (作物 B 的时间),A × B → C。
第 8 天到第 12 天 (作物 A 的时间),A × C → D。
花费 12 天得到作物 D 的种子。
输入描述
输入的第 1 行包含 4 个整数 N, M, K, T,N 表示作物种类总数 (编号 1 至 N),M 表示初始拥有的作物种子类型数量,K 表示可以杂交的方案数,T 表示目标种子的编号。
第 2 行包含 N 个整数,其中第 i 个整数表示第 i 种作物的种植时间 Ti(1≤Ti≤100)。
第 3 行包含 M 个整数,分别表示已拥有的种子类型 j (1≤Kj ≤M),K j 两两不同。
第 4 至 K + 3 行,每行包含 3 个整数 A, B,C,表示第 A 类作物和第 B 类作物杂交可以获得第 C 类作物的种子。
其中,1≤N≤2000,2≤M≤N,1≤K≤10 5 ,1≤T≤N, 保证目标种子一定可以通过杂交得到。
输出描述
输出一个整数,表示得到目标种子的最短杂交时间。
输出描述
输出一个整数,表示得到目标种子的最短杂交时间。
输入输出样例
输入:
6 2 4 6
5 3 4 6 4 9
1 2
1 2 3
1 3 4
2 3 5
4 5 6
输出:
16
样例说明
第 1 天至第 5 天,将编号 1 与编号 2 的作物杂交,得到编号 3 的作物种子。
第 6 天至第 10 天,将编号 1 与编号 3 的作物杂交,得到编号 4 的作物种子。
第 6 天至第 9 天,将编号 2 与编号 3 的作物杂交,得到编号 5 的作物种子。
第 11 天至第 16 天,将编号 4 与编号 5 的作物杂交,得到编号 6 的作物种子。
dfs自顶向下,用一个数组every表示得到每个节点的最短培育时间,一个数组flag表示每个节点是否已经得到。
从父节点x找每对子节点即杂交方案(每个作物可能由多对种子杂交达到,因为杂交方案数远大于种子类型数量),每遍历一次该种子x的杂交方案,更新一遍得到该种子x的最短培育时间。
设种子x的杂交方案为种子a,b,当前杂交方案的时间=a\b的最长培育时间+杂交得到a\b的最长时间。得到种子x的时间为every[x],min函数更新。
#define _CRT_SECURE_NO_WARNINGS
#include >
int dfs(int);
int main()
{
scanf("%d %d %d %d", &n, &m, &k, &t);
memset(every, 0x3f3f, sizeof(every));
//每种作物的时间
for(int i = 1; i <= n; i ++){
scanf("%d", ×[i]);
}
//已拥有的作物
for(int i = 0; i < m; i ++){
int tmp;
scanf("%d\n", &tmp);
flag[tmp] = 1;
every[tmp] = 0;
}
//杂交方案
for(int i = 0; i < k; i ++){
int a, b, c;
scanf("%d %d %d", &a, &b, &c);
ways[c].push_back(a);
ways[c].push_back(b);
}
printf("%d\n", dfs(t));
return 0;
}
int dfs(int i){
for(int j = 0; j < ways[i].size() - 1; j += 2){
int a = ways[i][j];
int b = ways[i][j + 1];
if(!flag[a]){
dfs(a);
}
if(!flag[b]){
dfs(b);
}
if(flag[a] && flag[b]){
flag[i] = 1;
every[i] = min(every[i], max(times[a], times[b]) + max(every[a], every[b]));
}
}
return every[i];
}
I 子串分值和(25分)
输入描述
输入一行包含一个由小写字母组成的字符串 S。
其中,1 ≤ n ≤ 105。
输出描述
输出一个整数表示答案。
输入输出样例
输入
ababc
输出
28
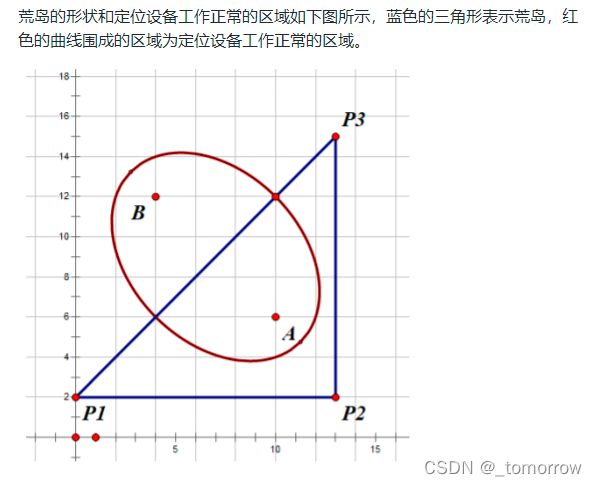
J 荒岛探测(25分)
题目描述

输入描述

输出描述
输出一行,包含一个实数,四舍五入保留 2 位小数,表示答案。
考虑到计算中的误差,只要你的输出与参考输出相差不超过 0.01 即可。
输入输出样例
输入:
10 6 4 12 12
0 2 13 2 13 15
输出:
39.99