【数据结构与算法】队列和栈的相互实现以及循环队列

一.用队列实现栈

1.题目描述

我们先看一下题目链接

2.思路分析

我们知道栈是后进先出的线性表，题目要求我们使用两个队列来实现，队列的特性是先进先出，从队尾进 队头出,图解如下:

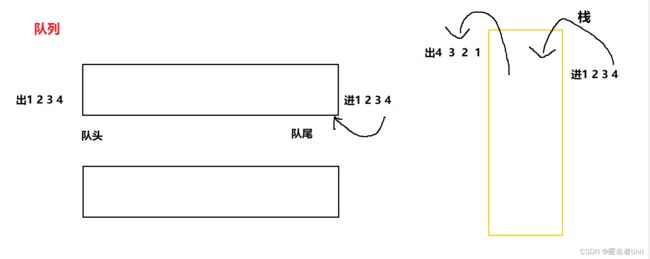
那我们如何向队列进元素1 2 3 4出队列是4 3 2 1的顺序呢。假设现在队列中有1 2 3 4:

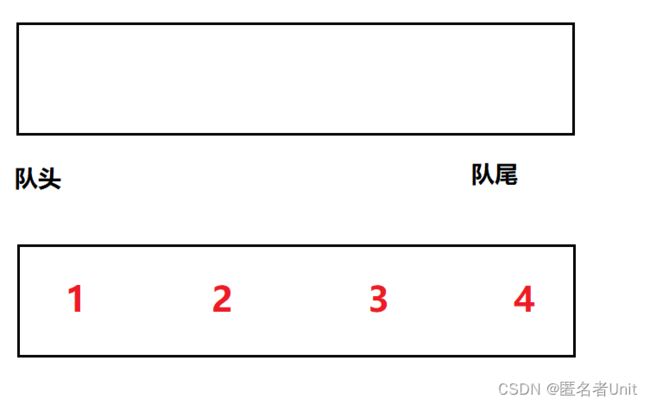
我们想让4先出队列的话，可以将前面的1 2 3先转移到另一个队列中，再出4，以此类推实现后进先拿出。使得一个队列为空用来出队列时倒元素的目的地，另一个不为空的队列用来插入数据。想要返回栈顶元素 只要返回非空队列的队尾元素即可。

3.代码实现

代码的实现，我们需要先手撕个队列包括队列的基本功能并且定义两个队列:

typedef int QDataType;

typedef struct QueueNode
{
	struct QueueNode* next;
	QDataType data;
}QNode;


typedef struct Queue
{
	QNode* head;
	QNode* tail;
	int size;
}Queue;

typedef struct {
    Queue q1;
    Queue q2;
} MyStack;
void QueueInit(Queue* pt);
void QueueDestroy(Queue* pt);

void QueuePush(Queue* pt, QDataType x);
void QueuePop(Queue* pt);

int QueueSize(Queue* pt);

bool QueueEmpty(Queue* pt);

QDataType QueueFront(Queue* pt);
QDataType QueueBack(Queue* pt);



void QueueInit(Queue* pt)
{
	assert(pt);

	pt->head = pt->tail = NULL;
	pt->size = 0;
}

void QueueDestroy(Queue* pt)
{
	assert(pt);
	QNode* cur = pt->head;

	while (cur)
	{
		QNode* next = cur->next;
		free(cur);
		cur = next;
	}
	pt->head = pt->tail = NULL;
	pt->size = 0;
}


void QueuePush(Queue* pt, QDataType x)
{
	QNode* newnode = (QNode*)malloc(sizeof(QNode));
	if (newnode == NULL)
	{
		perror("malloc fail");
		return;
	}

	newnode->next = NULL;
	newnode->data = x;

	if (pt->head == NULL)
	{
		assert(pt->tail == NULL);
		pt->head = pt->tail = newnode;
	}
	else
	{
		pt->tail->next = newnode;
		pt->tail = newnode;
	}

	pt->size++;

}


void QueuePop(Queue* pt)
{
	assert(pt);
	assert(pt->head != NULL);

	if (pt->head->next == NULL)
	{
		free(pt->head);
		pt->head = pt->tail = NULL;
	}
	else
	{
		QNode* next = pt->head->next;

		free(pt->head);
		pt->head = next;
	}
	pt->size--;
}


int QueueSize(Queue* pt)
{
	assert(pt);
	
	return pt->size;
}

bool QueueEmpty(Queue* pt)
{
	assert(pt);
	
	return pt->size == 0;
}

QDataType QueueFront(Queue* pt)
{
	assert(pt);
	assert(!QueueEmpty(pt));

	return pt->head->data;
}
QDataType QueueBack(Queue* pt)
{
	assert(pt);
	assert(!QueueEmpty(pt));

	return pt->tail->data;
}

紧接着即使栈的实现:

MyStack* myStackCreate() {
    MyStack*ptr=(MyStack*)malloc(sizeof(MyStack));
    if(ptr==NULL)
    {
        perror("malloc fail");
        return NULL;
    }
    QueueInit(&ptr->q1);
    QueueInit(&ptr->q2);

    return ptr;

}

void myStackPush(MyStack* obj, int x) {
    if(!QueueEmpty(&obj->q1))//向非空队列插入数据
    {
        QueuePush(&obj->q1,x);
    }
    else
    {
        QueuePush(&obj->q2,x);
    }
    
}

int myStackPop(MyStack* obj) {
    Queue* empty=&obj->q1;//先假设空与非空队列
    Queue* noempty=&obj->q2;

    if(!QueueEmpty(&obj->q1))
    {
        empty=&obj->q2;
        noempty=&obj->q1;
    }

    while(QueueSize(noempty)>1)
    {
        QueuePush(empty,QueueFront(noempty));
        QueuePop(noempty);
    }

    int ret=QueueFront(noempty);

    QueuePop(noempty);

    return ret;

}

int myStackTop(MyStack* obj) {
    if(!QueueEmpty(&obj->q1))
    {
        return QueueBack(&obj->q1);
    }
    else
    {
        return QueueBack(&obj->q2);
    }
}

bool myStackEmpty(MyStack* obj) {
    return QueueEmpty(&obj->q1)&&QueueEmpty(&obj->q2);//只有当两队列都为空的时候栈才为空
}

void myStackFree(MyStack* obj) {
    QueueDestroy(&obj->q1);
    QueueDestroy(&obj->q2);
    free(obj);
}

⛈二.用栈实现队列

☔1.题目描述

我们先看一下题目链接

☔2.思路分析

这题相反，需要我们实现两个栈来实现队列。究其本质就是使用两个后进先出显示先进先出，我们用图例来理解下:

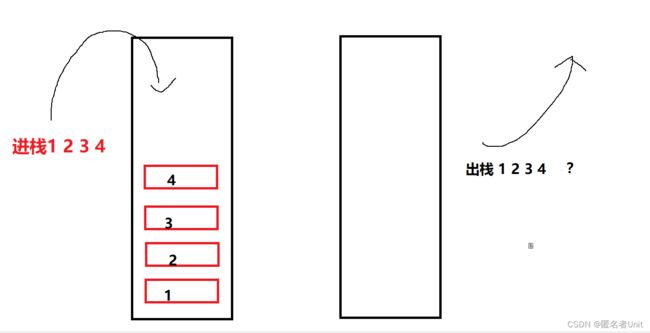
入栈1 2 3 4后出栈顺序为4 3 2 1我们可以依次顺序入到另一个栈中，再将数据从栈中弹出，即可做到出栈1 2 3 4的顺序。图示如下：

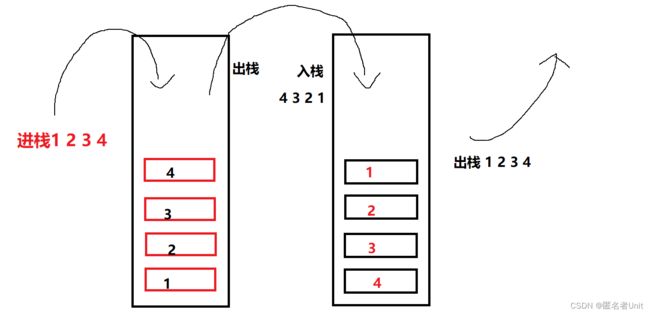
☔3.代码实现

代码还是需要先手撕个栈以及实现栈的基本功能并定义两个栈分别用来插入和删除:

typedef int STDataType;


typedef struct stack
{
	STDataType* a;
	STDataType top;
	STDataType capacity;
}ST;

void InitST(ST* s);//初始化栈
void DestroyST(ST* s);//销毁栈

void Push(ST* s, int x);//压栈
void Pop(ST* s);//出栈

bool STEmpty(ST* s);//判断栈是否为空栈
STDataType STSize(ST* s);//当前栈的元素个数
STDataType STTop(ST* s);//返回栈顶元素
void InitST(ST* s)
{
	assert(s);
	s->a = (STDataType*)malloc(sizeof(STDataType) * 4);
	if (s->a == NULL)
	{
		perror("malloc fail");
		return;
	}

	s->capacity = 4;
	s->top = -1;///top记录指向的当前元素
}

void DestroyST(ST* s)
{
	assert(s);
	s->capacity = 0;
	free(s->a);
	s->a = NULL;
	s->top = -1;
}

void Push(ST* s,int x)
{
	assert(s);

	if (s->top+1 == s->capacity)
	{
		s->a = (STDataType*)realloc(s->a,sizeof(STDataType)*s->capacity*2);
		if (s->a == NULL)
		{
			perror("malloc fail");
			return;
		}
		s->capacity *= 2;
	}
	s->a[s->top+1] = x;
	s->top++;

}

void Pop(ST* s)
{
	assert(s);
	assert(!STEmpty(s));

	s->top--;
}

bool STEmpty(ST* s)
{
	assert(s);
	if (s->top == -1)
		return true;
	return false;
}

STDataType STSize(ST* s)
{
	assert(s);

	return s->top + 1;
}

STDataType STTop(ST* s)
{
	assert(s);

	return s->a[s->top];
}

typedef struct {
    ST popst;
    ST pushst;
} MyQueue;

定义时我们就指定了用来插入的栈和删除的栈，我们在创建好自己的队列后，对队列进行插入操作时，只需要向pushst栈插入数据即可，另一个popst栈保持为空，在需要出队列时，将另一个栈的数据倒过来，再出数据 即可保证先进先出的顺序。

MyQueue* myQueueCreate() {
    MyQueue* ptr=(MyQueue*)malloc(sizeof(MyQueue));
    if(ptr == NULL)
    {
        perror("malloc fail");
        return NULL;
    }
    InitST(&ptr->popst);
    InitST(&ptr->pushst);
    return ptr;

}

void myQueuePush(MyQueue* obj, int x) {
    Push(&obj->pushst,x);
}

int myQueuePop(MyQueue* obj) {
    int ret=myQueuePeek(obj);
    Pop(&obj->popst);
    return ret;
}

int myQueuePeek(MyQueue* obj) {
    if(STEmpty(&obj->popst))
    {
        while(!STEmpty(&obj->pushst))
        {
            Push(&obj->popst,STTop(&obj->pushst));
            Pop(&obj->pushst);           
        }
    }
    return STTop(&obj->popst);
}

bool myQueueEmpty(MyQueue* obj) {
    return STEmpty(&obj->popst)&&STEmpty(&obj->pushst);
}

void myQueueFree(MyQueue* obj) {
    DestroyST(&obj->popst);
    DestroyST(&obj->pushst);
    free(obj);

}

三.实现循环队列

线性表有顺序存储和链式存储，栈是线性表，具有这两种存储方式。同样，队列作为一种特殊的线性表，也同样存在两种存储方式。队列的链式存储即是进行尾插头删的单链表，所以我们讲解队列的顺序存储———循环队列。
借助题目更好的讲解循环队列题目链接

首先我们创建结构体用来存储数据，其中包含指向存储数据地址的指针，记录队列有效长度的整形变量，还有两个记录循环队列头和尾数组下标的变量。

typedef struct {
    int *a;
    int rear;
    int front;
    int k;

} MyCircularQueue;

接着我们初始化队列，对于给定的有效长度k我们malloc比k多一的存储空间，方便表示存储满的情况另一种解决方法是增加size变量 用于记录当前数据个数。

MyCircularQueue* myCircularQueueCreate(int k) {
    MyCircularQueue* obj=(MyCircularQueue*)malloc(sizeof(MyCircularQueue));
    obj->rear=obj->front=0;
    obj->k=k;
    obj->a=(int*)malloc(sizeof(int)*(k+1));
    return obj;
}

队列为空的即是头尾指针指向同一地方的情况。

bool myCircularQueueIsEmpty(MyCircularQueue* obj) {
    return obj->front == obj->rear;
}

判断队列是否满，由于rear有可能比front大，也可能小，所以尽管他们只相差一个位置时就是满的情况，但可能相差整整一圈。为了避免判断错误，则需要取模判断。

bool myCircularQueueIsFull(MyCircularQueue* obj) {
    return (obj->rear+1)%(obj->k+1) == obj->front;
}

剩余代码

bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) {
    if(myCircularQueueIsFull(obj))
        return false;
    obj->a[obj->rear++]=value;
    obj->rear%=(obj->k+1);

    return true;
}

bool myCircularQueueDeQueue(MyCircularQueue* obj) {
    if(myCircularQueueIsEmpty(obj))
        return false;
    obj->front++;
    obj->front%=(obj->k+1);
    return true;
}

int myCircularQueueFront(MyCircularQueue* obj) {
    if(myCircularQueueIsEmpty(obj))
        return -1;
    return obj->a[obj->front];
}

int myCircularQueueRear(MyCircularQueue* obj) {
    if(myCircularQueueIsEmpty(obj))
        return -1;
    int x=obj->rear == 0? obj->k:obj->rear-1;//防止数据存储到最后一位
    return obj->a[x];
}



void myCircularQueueFree(MyCircularQueue* obj) {
    free(obj->a);
    free(obj);
}