【深度学习】rnn是什么?循环神经网络是什么？RNN前向传播。

循环神经网络

  通常卷积神经网络 适合处理图像问题，然而通常适合处理自然语言的网络是循环神经网络。rnn是所有基本网络，就像cnn 是很多复杂网络的基本原型。包括目前火热的自然语言处理的模型MLL,GPT等。rnn适合处理序列类数据，在语言模型与文本生成，以及机器翻译和语音识别等场景广泛使用。

1.循环神经网络原理

  循环神经网络能够对前面的信息进行“记忆”并且应用于当前输出的计算中，即隐藏层之间不再无连接。 某一个具体的隐藏层中的神经网络的神经元的输入不仅仅包含上一层的输出，还包括当前层上一个神经元的输出。
  假设给定一个长度为T的输入序列$\{x_0,x_1,...,x_t,...,x_T\}$,其中$x_t$表示在t时刻的输入特征向量，这里的t时刻，并不一定真的指的是时间，只是用来表明这是一个序列输入。现在要得到每个时刻的隐含特征$\{h_0,h_1,...,h_t,...,h_T\}$,这些隐含层特征那个与后面层的层的特征输入。如何采用传统的神经网络只需要进行一下计算。$$h_t=f(U{x}_t+b)$$其中f为非线性激活函数。但是，这样明显忽略了这是一个序列输入问题，即当丢失了序列中各个元素的依赖关系。对于循环神经网络，其在计算t时刻的特征时，不但考虑当前时刻的输入特征$x_t$,而且引入了前一个隐含特征$h_{t-1}$,计算如下。$$h_t=f(U{x}_t+W{h}_{t-1}+b)$$.
  显然，这样可以捕捉序列中的依赖关系，可以认为$h_{t-1}$是一个记忆特征，其提取了前面t-1个时刻输入的旧特征。可以称$h_{t-1}$为旧状态，称$h_t$为新状态。因此，循环神经网络特别适合解决序列问题。从结构上来看，循环神经网络可以看作是有环的神经网络（见图1）。

图1 循环神经网络结构（左）及其展开形式（右）

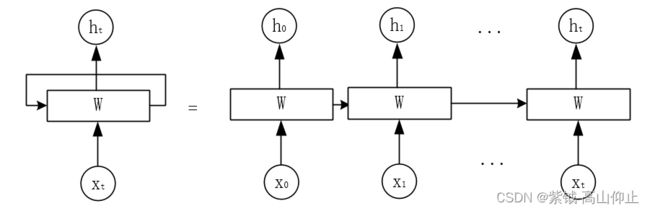
  不过，我们可以将其展开成普通的神经网络，准确地说，就是展开成t个普通地神经网络。但是这t个神经网络不是割裂的，他们使用的参数是相同的也是共享的，既权重共享。这样，在每一个时刻，循环神经网络执行的是相同的计算过程。

2.使用Numpy实现RNN层的前向传播

  为了实现RNN的层，通过Numpy包进行模拟一些平台的的构建层。RNN的输入是一个张量序列，我们输入一个形状为(sequence_length,input_feature)的二维张量。它对序列中每一个元素进行遍历，同时它会把前元素和上一个状态放在一起进行计算。对于第一个元素，由于没有上一个状态，所以需要初始化一个全零向量，然后将其作为初始状态。
  此时输入的矩阵为一个20个单词的矩阵，每一个单词的维度为5。状态权重w大小为1010，链接权重为510.输出为10的一个向量大小，表示最后一个隐藏层词语。前向传播输入结果为每一个隐含层的大小维度为20，10.

import numpy as np


class RNNlayer(object):
    def __init__(self,sequence_length:int,input_feature:int,output_feature:int):
        """

        :param sequence_length: 输入序列长度
        :param input_feature: 输入序列中每一个元素维度
        :param output_feature: 输出序列每一个元素维度
        """
        self.sequence_length = sequence_length
        self.input_feature = input_feature
        self.output_feature = output_feature
        #初始化0向量，
        self.state_t=np.zeros((output_feature,))
        #网络权重初始化
        self.W=np.random.uniform(size=(output_feature,input_feature))
        self.U=np.random.uniform(size=(output_feature,output_feature))
        self.b=np.random.uniform(size=(output_feature,))
    def _sigmoid(self,inputs:np.ndarray)->np.ndarray:
        """
        因为sigmoid激活函数是内部方法，所以函数名使用_
        :param inputs:输入特征
        :return: sigmoid的函数运算结果
        """
        sigm=1./(1.+np.exp(-inputs))
        return sigm
    def forward_propagation(self,inputs:np.ndarray)->np.ndarray:
        """
        前向传播
        :param inputs: 输入特征
        :return: 在该层中进行前向传播后的结果
        """
        output=[]
        #遍历输入特征，逐个计算对应的输出
        for input_t in inputs:
            # 有输入特征和前一个状态（前一个输出）计算当前的输出
            print(self.U,self.W,self.state_t)
            output_t=np.dot(self.W,input_t)+np.dot(self.U,self.state_t)+self.b
            #使用激活函数
            output_t=self._sigmoid(output_t)
            #将输出的保存到输入列表中
            output.append(output_t)
            # 将这次状态保存一边用于下次计算
            self.state_t=output_t
        return np.stack(output,axis=0)


if __name__ == '__main__':
    #初始化一个层
    rnn=RNNlayer(20,5,10)
    #随机初始化输入特征
    input_sequence=np.random.random((20,5))
    print(input_sequence)
    #进行前向传播
    output_sequence= rnn.forward_propagation(input_sequence)
    print(output_sequence)

3.RNN存在的问题

  虽然rnn处理时间序列效果非常好，但是其存在一定的问题。其中比较严重的问题是：处理长序列时，其容易出现梯度消失或者梯度爆炸。
（1）梯度爆炸：在训练过程梯度变大，大幅度更新网络参数 使得训练不稳定，可以通过截断或者压缩梯度解决。
（2）梯度消失：梯度变得非常小，导致更新网络过程时候变得非常缓慢，甚至停止更新参数。造成无法优化的局面。对于这个问题。通常使用变种网络，长短时间记忆网络lstm。它的出现解决了梯度消失问题。

4.小结

  本文介绍了rnn数据的输入结构以及rnn 用于时间序列的基本单元，并且通过一个numpy的前向传播算法实现了网络的计算。对于rnn如何进行参数更新，后续继续有相关博客进行讲解。