代码随想录算法训练营第二十八天 | 93. 复原 IP 地址、78. 子集、90. 子集 II

93. 复原 IP 地址

回溯三部曲

1、递归函数返回值及参数

vector result; //存放结果集
//start表示起始位置，point记录加入的‘.’的数量
void backtracking(string& s, int start, int point)

2、终止条件------当加入‘.’的数量为三时，此时对最后一段进行判断是否合法

if (point == 3) {
    //检查最后一段位是否合法
    if (isValid(s, start, s.size() - 1)) {
        result.push_back(s);
    }
    return ;
}

3、单次搜索过程------

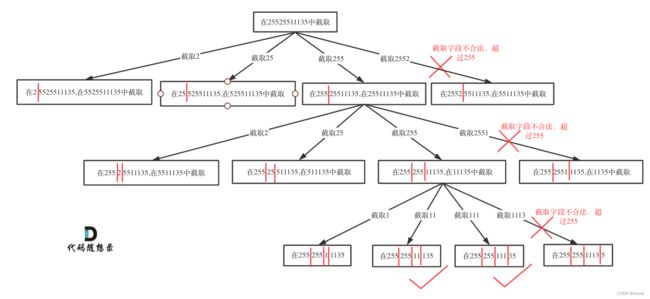
在for (int i = startIndex; i < s.size(); i++)循环中 [startIndex, i] 这个区间就是截取的子串，需要判断这个子串是否合法。

如果合法就在字符串后面加上符号.表示已经分割。

如果不合法就结束本层循环，如图中剪掉的分支：

然后就是递归和回溯的过程：

递归调用时，下一层递归的startIndex要从i+2开始（因为需要在字符串中加入了分隔符.），同时记录分割符的数量pointNum 要 +1。

回溯的时候，就将刚刚加入的分隔符. 删掉就可以了，pointNum也要-1。

for (int i = startIndex; i < s.size(); i++) {
    if (isValid(s, startIndex, i)) { // 判断 [startIndex,i] 这个区间的子串是否合法
        s.insert(s.begin() + i + 1 , '.');  // 在i的后面插入一个逗点
        pointNum++;
        backtracking(s, i + 2, pointNum);   // 插入逗点之后下一个子串的起始位置为i+2
        pointNum--;                         // 回溯
        s.erase(s.begin() + i + 1);         // 回溯删掉逗点
    } else break; // 不合法，直接结束本层循环
}

判断子串是否合法

//判断一段区间上值是否合法;
    bool isValid(const string& s, int start, int end) {
        if (start > end) {
            return false;
        }
        //段位以0为开头的数字不合法
        if (s[start] == '0' && start != end) {
            return false;
        }
        int num = 0;
        for (int i = start; i <= end; i++) {
            //段位里有非正整数字符不合法
            if (s[start] > '9' || s[start] < '0') {
                return false;
            }
            num = num * 10 + (s[i] - '0');
            // 段位如果大于255了不合法
            if (num > 255) {
                return false;
            }
        }
        return true;
    }

本题代码如下：

class Solution {
public:
    vector result; //存放结果集
    //start表示起始位置，point记录加入的‘.’的数量
    void backtracking(string& s, int start, int point) {
        if (point == 3) {
            //检查最后一段位是否合法
            if (isValid(s, start, s.size() - 1)) {
                result.push_back(s);
            }
            return ;
        }
        //
        for (int i = start; i < s.size(); i++) {
            if (isValid(s, start, i)) { //判断该区间是否合法，合法则加入<.>
                point++;
                s.insert(s.begin() + i + 1 , '.');  // 在i的后面插入一个逗点
                backtracking(s, i + 2, point);
                point--; //回溯
                s.erase(s.begin() + i + 1);
            } else {
                break;
            }
        }
    }
    //判断一段区间上值是否合法;
    bool isValid(const string& s, int start, int end) {
        if (start > end) {
            return false;
        }
        //段位以0为开头的数字不合法
        if (s[start] == '0' && start != end) {
            return false;
        }
        int num = 0;
        for (int i = start; i <= end; i++) {
            //段位里有非正整数字符不合法
            if (s[start] > '9' || s[start] < '0') {
                return false;
            }
            num = num * 10 + (s[i] - '0');
            // 段位如果大于255了不合法
            if (num > 255) {
                return false;
            }
        }
        return true;
    }

    vector restoreIpAddresses(string s) {
        result.clear();
        if (s.size() < 4 || s.size() > 12) return result; // 算是剪枝
        backtracking(s, 0, 0);
        return result;
    }
};

78. 子集

回溯三部曲：

1、递归函数返回值及参数

    vector> result; //存放结果集
    vector path; //存放单次结果

    void backtracking(vector& nums, int start)

2、终止条件------本题没有终止条件，每次把path放入结果集中即可

result.push_back(path);

3、单次搜索过程------每次把元素放入path中，回溯

        for (int i = start; i < nums.size(); i++) {
            path.push_back(nums[i]);
            backtracking(nums, i + 1);
            path.pop_back();
        }

本题代码如下：

class Solution {
public:
    vector> result; //存放结果集
    vector path; //存放单次结果

    void backtracking(vector& nums, int start) {
        result.push_back(path);
        for (int i = start; i < nums.size(); i++) {
            path.push_back(nums[i]);
            backtracking(nums, i + 1);
            path.pop_back();
        }
    }

    vector> subsets(vector& nums) {
        result.clear();
        path.clear();
        backtracking(nums, 0);
        return result;
    }
};

90. 子集 II

本题在上一题的基础上增加了重复元素，借助一个数组实现去重操作

本题代码如下：

class Solution {
public:

    vector> result; //存放结果集
    vector path; //存放单次结果

    void backtracking(vector& nums, int start, vector& used) {
        result.push_back(path);
        for (int i = start; i < nums.size(); i++) {
            // used[i - 1] == true，说明同一树枝candidates[i - 1]使用过
            // used[i - 1] == false，说明同一树层candidates[i - 1]使用过
            // 而我们要对同一树层使用过的元素进行跳过
            if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) continue;
            path.push_back(nums[i]);
            used[i] = true;
            backtracking(nums, i + 1, used);
            used[i] = false;
            path.pop_back();
        }
    }

    vector> subsetsWithDup(vector& nums) {
        result.clear();
        path.clear();
        vector used(nums.size(), false);
        sort(nums.begin(), nums.end()); // 去重需要排序
        backtracking(nums, 0, used);
        return result;
    }
};