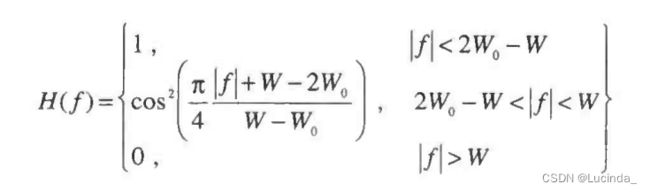数字通信学习笔记——基带信号解调
“外差”是指一种“频率转换”或“混频”的信号处理过程，可以实现信号的频谱搬移。
对线性系统来说，有如下等价定理：
先对带通信号做线性处理，再用外差法将信号转换为基带信号；其结果与先用外差法将信号转换为基带信号，再对基带信号做相应线性处理一致。由此可得，可以把大部分数字通信系统当作基带系统进行描述和分析。
本笔记中，“解调”指信号波形的恢复（恢复为无失真基带脉冲），“检测”指采样判决过程。
由于信号在传输过程中受到噪声干扰，因此接收矢量是发送信号矢量和噪声矢量的合成，噪声是加性高斯噪声，接收信号在信号空间中表现为以参考信号为中心的云状分布。
白噪声的方差：高斯白噪声的方差为无穷大，但经过滤波后的高斯白噪声的方差是有限的，为
信噪比：
模拟通信的信噪比SNR：信号平均功率与噪声平均功率的比值。
数字通信中，常用信噪比的归一化形式 
作为性能指标。
为每比特能量，等于信号能量S与每比特持续时间
的乘积；
是噪声功率谱密度，等于噪声功率N与带宽W之比；每比特持续时间 与比特速率
互为倒数，因此有下式：
为强调 是S/N的归一化带宽和比特率形式，上式也可写为：
数字通信系统性能最重要的度量之一就是误码率
与 的关系曲线。 是无量纲的。
匹配滤波器
匹配滤波器是指对于给定的码元波形，使得输出信噪比最大的线性滤波器。
匹配滤波器的冲激响应是信号s(t)的镜像信号在时间上再平移一个码元持续时间T。
码间串扰
由于系统滤波作用，脉冲出现拖尾占据了相邻码元间隔，从而干扰了信号检测过程，造成误码性能降低，这类干扰称为码间串扰。
即使没有噪声，滤波和信道引起的失真也会导致码间串扰。
奈奎斯特研究了接收端不产生码间串扰的接收脉冲形状问题，证明了要使码元速率为
码元/s的信号不存在码间串扰，理论上所需的最小系统带宽为
Hz。最小系统带宽成立的条件是，系统传输函数是矩形函数。
“奈奎斯特滤波器”和“奈奎斯特脉冲”常用于描述在采样点无码间串扰的典型滤波器和脉冲。奈奎斯特滤波器的频率传输函数可以表示为矩形函数和任意一个实偶对称频率函数的卷积；奈奎斯特脉冲可以表示为sinc(t/T)函数与另一个时间函数的乘积。（说白了都是时域相乘）
降低码间串扰的脉冲整形
当接收滤波器可以同时补偿发射机和信道产生的失真时，就称其为均衡滤波器。
常用的奈奎斯特类型（在采样时刻无码间串扰）传输函数是升余弦滤波器，表达式为：
其中，W是绝对带宽，
代表矩形频谱对应的最小奈奎斯特带宽和升余弦频谱的-6dB带宽（半振幅点），差值
是“超量带宽”，即超出最小奈奎斯特带宽的部分。
滚降系数定义为
对应的冲激响应为：
无论滚降系数为何值，在每个脉冲的采样时刻其他脉冲的值都为0.
由于滚降系数的存在，无码间串扰条件下所需带宽与码元传输速率的关系是：
对带通调制信号，如ASK,PSK，需要的传输带宽是相应基带信号的2倍，此时双边带带宽与码元速率的关系为：
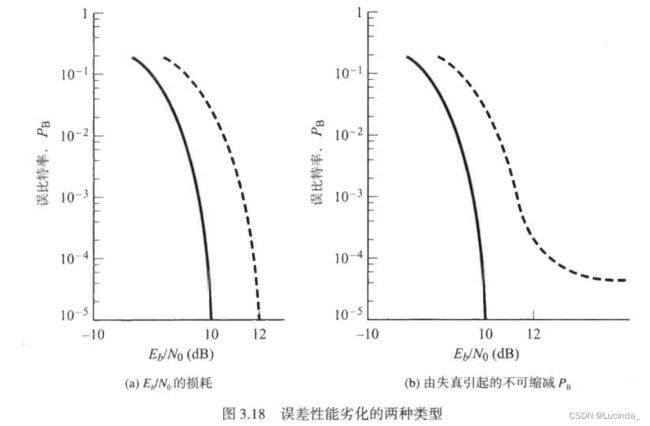
差错性能劣化的两种类型
一是由于接收信号能量的降低或噪声能量的增加导致信噪比
减小，从而使系统性能下降；另一种是因为信号失真，如由于码间串扰引起的失真。
对于由失真引起的性能下降，当曲线达到不能再减小的 点时，增大 也无法解决串扰问题，此时会采用均衡。
匹配滤波器与一般滤波器的对比：
一般滤波器：在通带内有近似均匀的增益且保持线性的相频特性，在阻带范围内频谱分量尽量衰减到最小。尽量保持有用信号的时域或频域结构。
匹配滤波器：在存在高斯白噪声的条件下使已知信号的信噪比最大。通过集中与之相匹配的信号能量来改变信号的时间结构，并在输出码元的末端获得振幅的最大值。