对力扣27.移除元素 力扣26删除有序数组中的重复项 力扣189. 轮转数组 力扣面试题 17.04. 消失的数字 力扣728. 自除数的复盘总结

前言

---

本文是我对平时做力扣题的题解思考，做题之后的复盘总结。如果本文对你也有所帮助的话，麻烦点个赞吧!谢谢！

---

1.力扣27.移除元素

1.题目分析

题目链接直接点击

这道题是要求移除数组中指定的元素val。首先我们在首先实现顺序表的时候就知道了数组中的元素是不能删除只能覆盖的。这道题如果直接开另外一个空间对元素遍历进行数据的移除也是可行的，但是题目要求了我们原地移除，也就是不开额外的空间。那么也就是说要对原数组进行数据的覆盖。那么怎么覆盖呢？这里介绍一种类似于双指针的方法。就是定义两个下标变量。最开始的时候两个下标都指向数组首位置，让一个下标先跑，如果遇到到val，后跑的下标变量不移动，先跑的继续移动。如果先跑的下标指向的元素不是val，就把先跑的下标所指向的元素赋值给后跑的下表所指向的位置。，然后先跑的和后跑的下标都移动一次，直到先跑的下标遍历完整个数组。这样操作之后就移除了指定的val。

有了上述思考代码就很好写出来

2. 代码示例与总结

nt removeElement(int* nums, int numsSize, int val){
  int j=0;
  int i=0;
  while(j<numsSize)
  {
      if(nums[j]!=val)
      {
          nums[i]=nums[j];
          j++;
          i++;
      }
      else
      {
          j++;
      }
  }
  return i;
}

i就是蓝色箭头j就是绿色箭头，可以看到每次都是先进行判断再进行下标的移动的，j无论什么情况下都要进行移动，相当于是遍历了数组。同时这个函数的返回值是返回移除val后元素个数，因为每次都是移动元素完了在进行下标的移动，所以直接返回i即可。

---

2.力扣26删除有序数组中的重复项

1.题目分析

题目链接直接点击

这道题目和上述的题目的解法类似，都是通过类似于双指针的做法来解题。这道的题要求是移除重复的元素。我们还是定义两个下标变量，最开始两个下标都指向同一个位置，一个跑在前，一个跑在后面，因为这是找重复的数字，所以第一个数字肯定是不用判断的直接放进数组例即可，通过遍历判断后面的元素是否和第一个相同。如果不相同就放进数组，接着遍历即可。如果相同了，跑在前面的下标继续移动，但是跑在后面的下标不移动，遍历完整个数组就完成了重复元素的移除。

码示例与总结

int removeDuplicates(int* nums, int numsSize){
    int i=1;
    int j=1;
    while(j<numsSize)
     {
         if(nums[i-1]!=nums[j])
           {
               nums[i]=nums[j];
               i++;
               j++;
           }
         else
         {
           j++;
         }
     }
  return i;
}

这道题和刚才的题做法有点像，但是有很多细节要考虑。首先第一道题两个下标的起始位置都是指向数组起始位置的，这道题我将起始位置设在第二个元素的位置，这是因为第一个元素肯定不用考虑的，考虑的是第一个元素后面有没有和第一个元素重复的元素。两个下标指向的元素从一开始都要进行判断，和上面的题一样都是先判断再移动。按照顺序，要判断第二个元素和第一个元素是不是相等的。因此，i是要减1的，每次j都要和它后面一个元素进行判断，这个i的作用就是用来指向j后面的一个元素进行判断，当遇到了重复的元素，i就不能再移动了，只用移动j即可。因为这是相同的元素不能放进数组，i所指向的位置应该存放下一个不相同的元素。每次判断不是重复数字后，i都会指向下一个即将放置元素的位置，这个函数返回值是返回移除后重复的元素后，数组元素的个数，所有只用返回i即可。

---

3.力扣189. 轮转数组

1.题目分析

题目链接直接点击

之前的博客中介绍过一道左旋字符串的题和这个题目的基本是差不多的。这道题先介绍暴力解法，暴力解法就是按照题目的要求直接挪动数组元素即可。假设旋转一次，我们先将最后末尾的元素保存下来，再从倒数二的位置开始将倒数第二的位置的元素移动到最后一个位置即可。然后将倒数第3位置的元素移动到倒数第二的位置，这样依次往后移动，直到首位置的元素移动到正数第二的位置上，最后将保存的末尾的元素移动到数组首位置。之所以倒着移动，是因为正着移动会造成元素覆盖的情况，元素不能完整的迁移到指定的位置。这样移动算一次旋转。因为有k次旋转，所以像这样的挪动需要进行k次，但是我们如果一个数组有7个元素，旋转7次后就相当于没有挪动，还是保持原样，所以只用对k进行取余操作。

代码示例

void rotate(int* nums, int numsSize, int k){

  for( int j=k%numsSize;j>0;j--)
  {  
      int tem=nums[numsSize-1];
      for(int i=numsSize-1;i>=1;i--)
     {
        nums[i]=nums[i-1];
      }
      nums[0]=tem;
   }
}

虽然这中方法可以到达旋转的目的，但是时间复杂度过高了，会超出时间限制，通不过测试

---

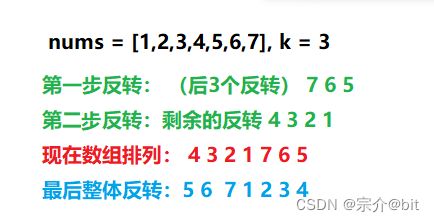
接着介绍一种比较巧妙的方法，3步反转法。以示例为例nums = [1,2,3,4,5,6,7], k = 3。1 2 3 4先反转成 4 3 2 1。接着5 6 7反转成 7 6 5这样数组元素就成了4 3 2 1 7 6 5，然后整体反转 5 6 7 1 2 3 4。这样就和3次反转的效果一样。

2.代码示例与总结

void  move(int *nums,int left,int right)
{
    while(left<right)
    {
       int tem=nums[left];
       nums[left]=nums[right];
       nums[right]=tem;
       left++;
       right--;
    }
}

void rotate(int* nums, int numsSize, int k){
    int number=k%numsSize;
    move( nums,numsSize-number,numsSize-1);
    move(nums,0,numsSize-number-1);
    move(nums,0,numsSize-1);
 
}

这道题和左旋字符串做法类似，这个像是右旋。关于旋转分隔位置不确定的话，可以用给出的数组示例自己推导演示。就可以知道在哪里进行数组分割旋转了。在旋转之前记得将k取余，原因在上面已经讲过了。

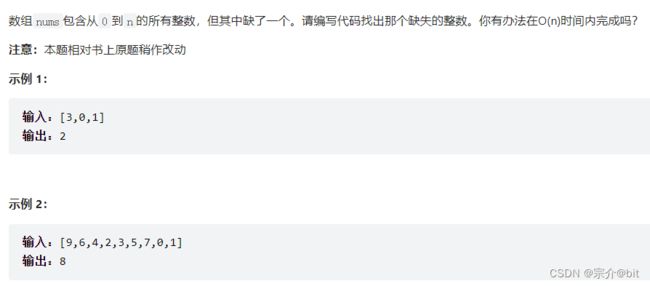
4.力扣面试题 17.04. 消失的数字

1.题目分析

题目链接直接点击

这道题介绍两种做法。这种类型的题目其实之前也有介绍。无非就算开一个数组，将原数组元素转成另一个数组下标的做法，还有就是利用异或位运算来解决。一般这种题目比较优的解法就是异或解决。先介绍开数组的方法

代码示例

int missingNumber(int* nums, int numsSize){
    int* arr=(int*)calloc(numsSize+1,4);
    for(int i=0;i<numsSize;i++)
      {
          arr[nums[i]]=1;
      }
      int j=0;
      for( j=0;j<numsSize;j++)
         {
             if(arr[j]!=1)
             {
                 break;
             }
         }
  return j;
}

这种做法一定要注意，所开的数组的下标最大值一定是大于等于原数组元素中的最大值的，这样才能顾及到原数组的所有的元素。

---

接着介绍异或，之前我们做过在一组非负整型数据中找到唯一个出现奇数次的数直接异或遍历即可。这道题是缺少了一个数字，如果我们将0到n的数全部异或一遍再和这个数组所有元素异或一遍，相当于只有缺失的数字出现了一次也就是奇数次，其余的数据都出现了两次也就是偶数次。这样问题就很好解决了。

2.代码示与例总结

int missingNumber(int* nums, int numsSize){
    int ret=0;
    for(int i=1;i<=numsSize;i++)
    {
        ret^=i;
    }
    for(int i=0;i<numsSize;i++)
    {
        ret^=nums[i];
    }
 return ret;
}

当题目做多了以后，很容易发现很多题其实都是同一种题。或者通过某些转化就成另一个原来见过的问题。要善于总结。

---

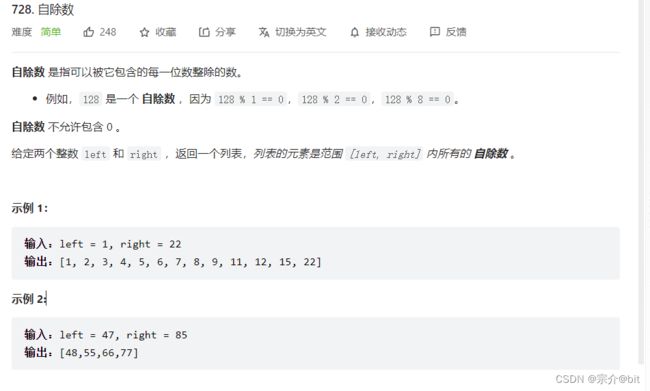
5.力扣728. 自除数

1.题目分析

题目链接直接点击

这道题的意思就是如果一个整数可以整除掉所有组成它的数字，这个数就是自除数，0除外。这道题给出的数据范围不包含0，所以不用考虑0的情况。要判断是否是自除数，就得把一个数的所有组成它的数字都找出来。然后让这个数对每个数字进行取余计数。既然要得到每个组成它的数字，肯定要对这个数进行运算，但是同时在判断的时候还要用到这个数字，所以需要用个临时变量来保存这个数字，用这个临时变量求出每一位数字，在进行判断。

2.代码示例与总结

int* selfDividingNumbers(int left, int right, int* returnSize){
    int *nums=malloc((1000)*sizeof(int));
    *returnSize=0;
    while(left<=right)
    { 
        int tem =left;
        while(tem%10)
        {
            if(left%(tem%10)!=0)
            {  
                
                break;
            }
            tem /=10;
        }
        if(!tem)
        {
            nums[*returnSize]=left;
            (*returnSize)++;
        }
     left++;
    }
 return nums;
}

(tem%10) ;tem /=10;就是在求数字的每一位数
以123为例.123%10=3;123/10=12,12%10=2;12/10=1,1%10=1;这样1 2 3 全部求出来了。直到tem成了0跳出循环这个时候说明这个数能整除所有组成它的数字。如果在tem变成0之前跳出了循环，这声明是遇到了break，也就是说这个数字不能整除组成它的某个数字，这个数就不是自除数。每次循环到最后left++,及时更新。同时要注意tem要创建在循环题内，创建时直接将left的初值给它。这样保证每次关心left的时候，tem也能跟着更新。

---

6.总结

本文简单的对我做过的部分力扣题进行了简单的总结复盘总结。如有错误欢迎指正！