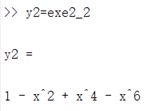MATLAB使用符号工具箱计算函数的5阶麦克劳林多项式的四种方法(附指定阶数、指定点的泰勒展开)
此篇博客是对MATLAB符号工具箱taylor的用法进行总结和拓展。
先通过两个具体的例子进行讲述:
1.MATLAB中使用符号工具箱计算exp(x)的5阶麦克劳林多项式
%计算exp(x)的5阶麦克劳林多项式
>> syms x
s = taylor(exp(x))
s = taylor(exp(x),'order',6)
s = taylor(exp(x),x,0,'order',6)
s = taylor(exp(x),'order',6,'ExpansionPoint',0)
%运行的结果均为:
s =
1 + x + x^2/2 + x^3/6 + x^4/24 + x^5/120
2.MATLAB中使用符号工具箱计算sin(x)的5阶麦克劳林多项式
%计算sin(x)的5阶麦克劳林多项式
>> syms x
>> s = taylor(sin(x))
s = taylor(sin(x),'order',6)
s = taylor(sin(x),x,0,'order',6)
s = taylor(sin(x),'order',6,'ExpansionPoint',0)
%运行的结果均为:
s =
x^5/120 - x^3/6 + x
展开阶数:(展开越多阶数,图像越接近原式子)
要让我们展开多项式的图像更加接近sin(x),我们必须要让MATLAB返回更多项,假设我们要得到m项展开式,使用order命令,后面跟上想要展开的阶数m-1(m项)。我们知道,泰勒公式可以在任意一点展开,在零点处展开我们称为麦克劳林公式。
syms x
s = taylor(sin(x),x,0,'order',6)
还有一个问题是我们的泰勒展开式的阶数是从高到低,这不是我们想要的,我们要让它从低到高,可以使用sympref命令:
sympref('PolynomialDisplayStyle','ascend');
同时,我们还可以使用命令’ExpansionPoint’在指定点展开。例如上述的两个例子当中,s1命令的意思就是在点x=0处,求解5阶泰勒展开式:
syms x
s1 = taylor(exp(x),'order',6,'ExpansionPoint',0)
s2 = taylor(sin(x),'order',6,'ExpansionPoint',0)
另附数学实验的一个题目和求解参考答案:(可以看到,最终的结果的阶数是从低到高的)
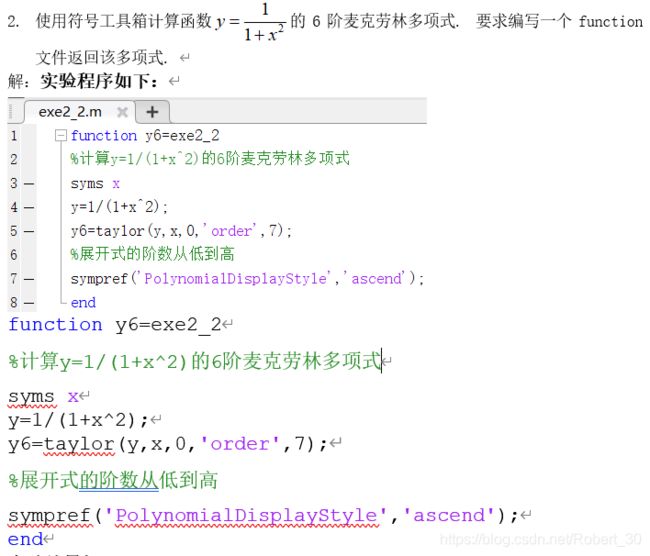
function y6=exe2_2
%计算y=1/(1+x^2)的6阶麦克劳林多项式
syms x
y=1/(1+x^2);
y6=taylor(y,x,0,'order',7);
%展开式的阶数从低到高sympref('PolynomialDisplayStyle','ascend');
end
y2 =
1 - x^2 + x^4 - x^6
参考博客:MATLAB与高等数学–泰勒展开