Latent Semantic Analysis (LSA) Tutorial 潜语义分析LSA介绍 第二部分

Part 2 - Modify the Counts with TFIDF

计算TFIDF替代简单计数

In sophisticated Latent Semantic Analysis systems, the raw matrix countsare usually modified so that rare words are weighted more heavily than commonwords. For example, a word that occurs in only 5% of the documents shouldprobably be weighted more heavily than a word that occurs in 90% of thedocuments. The most popular weighting is TFIDF (Term Frequency - InverseDocument Frequency). Under this method, the count in each cell is replaced bythe following formula.

在复杂的LSA系统中，为了重要的词占据更重的权重，原始矩阵中的计数往往会被修改。例如，一个词仅在5%的文档中应该比那些出现在90%文档中的词占据更重的权重。最常用的权重计算方法就是TFIDF（词频-逆文档频率）。基于这种方法，我们把每个单元的数值进行修改：

TFIDF_i,j = ( N_i,j / N_*,j ) * log( D / D_i) where

• N_i,j = the number of times word i appears in document j (the original cell count).
• N_*,j = the number of total words in document j (just add the counts in column j).
• D = the number of documents (the number of columns).
• D_i = the number of documents in which word i appears (the number of non-zero columns in row i).

N_ij = 某个词i出现在文档j的次数（矩阵单元中的原始值）
N_*j= 在文档j中所有词的个数（就是列j上所有数值的和）
D = 文档个数（也就是矩阵的列数）
D_i= 包含词i的文档个数（也就是矩阵第i行非0列的个数）

In this formula, words that concentrate in certain documents areemphasized (by the N_i,j / N_*,jratio) and words that onlyappear in a few documents are also emphasized (by the log( D / D_i )term).

Since we have such a small example, we will skip this step and move on theheart of LSA, doing the singular value decomposition of our matrix of counts.However, if we did want to add TFIDF to our LSA class we could add the followingtwo lines at the beginning of our python file to import the log, asarray, andsum functions.

在这个公式里，在某个文档中密集出现的词被加强（通过N_ij/N_*j），那些仅在少数文档中出现的词也被加强（通过log(D/D_i)）

因为我们的例子过小，这里将跳过这一个步骤直接进入LSA的核心部分，对我们的计数矩阵做SVD。然而，如果我们需要增加TFIDF到这个LSA类中，我们需要加入以下两行代码。

 

from math importlog
from numpy import asarray, sum

from math importlog from numpy import asarray, sum

 

Then we would add the following TFIDF method to our LSA class. WordsPerDoc(N_*,j) just holds the sum of each column, which is the total numberof index words in each document. DocsPerWord (D_i) uses asarray tocreate an array of what would be True and False values, depending on whetherthe cell value is greater than 0 or not, but the 'i' argument turns it into 1'sand 0's instead. Then each row is summed up which tells us how many documentseach word appears in. Finally, we just step through each cell and apply theformula. We do have to change cols (which is the number of documents) into afloat to prevent integer division.

接下来需要增加下面这个TFIDF方法到我们的LSA类中。WordsPerDoc 就是矩阵每列的和,也就是每篇文档的词语总数。DocsPerWord 利用asarray方法创建一个0、1数组（也就是大于0的数值会被归一到1），然后每一行会被加起来，从而计算出每个词出现在了多少文档中。最后，我们对每一个矩阵单元计算TFIDF公式

[python] view plain copy print ?

def TFIDF(self):

    WordsPerDoc = sum(self.A, axis=0)

    DocsPerWord = sum(asarray(self.A > 0,'i'), axis=1)

    rows, cols = self.A.shape

    for i in range(rows):

        for j in range(cols):

            self.A[i,j] = (self.A[i,j] /WordsPerDoc[j]) * log(float(cols) / DocsPerWord[i])

Part 3 - Usingthe Singular Value Decomposition

使用奇异值分解

Oncewe have built our (words by titles) matrix, we call upon a powerful but littleknown technique called Singular Value Decomposition or SVD to analyze thematrix for us. The"SingularValue Decomposition Tutorial" is a gentle introduction for readers that want to learn moreabout this powerful and useful algorithm.

一旦我们建立了词到标题的矩阵，我们就能够利用一个非常强大的工具“奇异值分解”去为我们分析这个矩阵。“"Singular Value DecompositionTutorial”是其的一个介绍。

Thereason SVD is useful, is that it finds a reduced dimensional representation ofour matrix that emphasizes the strongest relationships and throws away thenoise. In other words, it makes the best possible reconstruction of the matrixwith the least possible information. To do this, it throws out noise, whichdoes not help, and emphasizes strong patterns and trends, which do help. Thetrick in using SVD is in figuring out how many dimensions or"concepts" to use when approximating the matrix. Too few dimensionsand important patterns are left out, too many and noise caused by random wordchoices will creep back in.

SVD非常有用的原因是，它能够找到我们矩阵的一个降维表示，他强化了其中较强的关系并且扔掉了噪音（这个算法也常被用来做图像压缩）。换句话说，它可以用尽可能少的信息尽量完善的去重建整个矩阵。为了做到这点，它会扔掉无用的噪音，强化本身较强的模式和趋势。利用SVD的技巧就是去找到用多少维度（概念）去估计这个矩阵。太少的维度会导致重要的模式被扔掉，反之维度太多会引入一些噪音。

TheSVD algorithm is a little involved, but fortunately Python has a libraryfunction that makes it simple to use. By adding the one line method below toour LSA class, we can factor our matrix into 3 other matrices. The U matrixgives us the coordinates of each word on our “concept” space, the Vt matrixgives us the coordinates of each document in our “concept” space, and the Smatrix of singular values gives us a clue as to how many dimensions or“concepts” we need to include.

这里SVD算法介绍的很少，但是幸运的是python有一个简单好用的类库（scipy不是太好装）。如下述代码所示，我们在LSA类中增加了一行代码，这行代码把矩阵分解为另外三个矩阵。矩阵U告诉我们每个词在我们的“概念”空间中的坐标，矩阵Vt 告诉我们每个文档在我们的“概念”空间中的坐标，奇异值矩阵S告诉我们如何选择维度数量的线索（需要去研究下为什么）。

def calc(self):

self.U, self.S, self.Vt = svd(self.A)

def calc(self): self.U, self.S, self.Vt = svd(self.A)

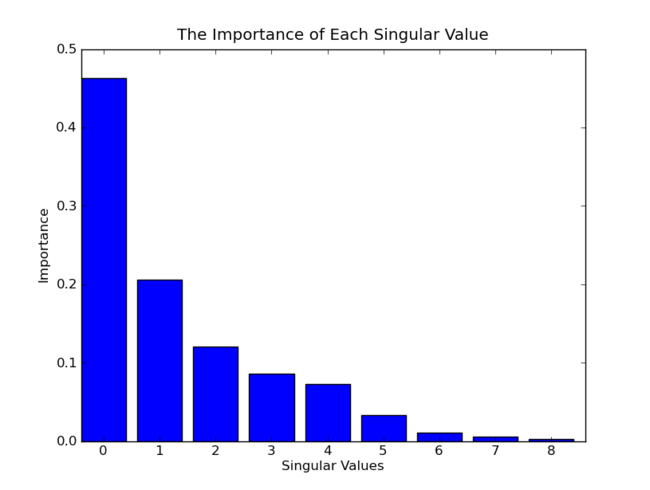
Inorder to choose the right number of dimensions to use, we can make a histogramof the square of the singular values. This graphs the importance each singularvalue contributes to approximating our matrix. Here is the histogram in ourexample.

为了去选择一个合适的维度数量，我们可以做一个奇异值平方的直方图。它描绘了每个奇异值对于估算矩阵的重要度。下图是我们这个例子的直方图。（每个奇异值的平方代表了重要程度，下图应该是归一化后的结果）

Forlarge collections of documents, the number of dimensions used is in the 100 to500 range. In our little example, since we want to graph it, we’ll use 3dimensions, throw out the first dimension, and graph the second and thirddimensions.

对于大规模的文档，维度选择在100到500这个范围。在我们的例子中，因为我们打算用图表来展示最后的结果，我们使用3个维度，扔掉第一个维度，用第二和第三个维度来画图（为什么扔掉第一个维度？）。

Thereason we throw out the first dimension is interesting. For documents, thefirst dimension correlates with the length of the document. For words, it correlateswith the number of times that word has been used in all documents. If we hadcentered our matrix, by subtracting the average column value from each column,then we would use the first dimension. As an analogy, consider golf scores. Wedon’t want to know the actual score, we want to know the score aftersubtracting it from par. That tells us whether the player made a birdie, bogie,etc.

我们扔掉维度1的原因非常有意思。对于文档来说，第一个维度和文档长度相关。对于词来说，它和这个词在所有文档中出现的次数有关（为什么？）。如果我们已经对齐了矩阵（centering matrix），通过每列减去每列的平均值，那么我们将会使用维度1（为什么？）。类似的，像高尔夫分数。我们不会想要知道实际的分数，我们想要知道减去标准分之后的分数。这个分数告诉我们这个选手打到小鸟球、老鹰球（猜）等等。

Thereason we don't center the matrix when using LSA, is that we would turn asparse matrix into a dense matrix and dramatically increase the memory andcomputation requirements. It's more efficient to not center the matrix and thenthrow out the first dimension.

我们没有对齐矩阵的原因是，对齐后稀疏矩阵会变成稠密矩阵，而这将大大增加内存和计算量。更有效的方法是并不对齐矩阵并且扔掉维度1.

Hereis the complete 3 dimensional Singular Value Decomposition of our matrix. Eachword has 3 numbers associated with it, one for each dimension. The first numbertends to correspond to the number of times that word appears in all titles andis not as informative as the second and third dimensions, as we discussed.Similarly, each title also has 3 numbers associated with it, one for eachdimension. Once again, the first dimension is not very interesting because ittends to correspond to the number of words in the title.

下面是我们矩阵经过SVD之后3个维度的完整结果。每个词都有三个数字与其关联，一个代表了一维。上面讨论过，第一个数字趋向于和该词出现的所有次数有关，并且不如第二维和第三维更有信息量。类似的，每个标题都有三个数字与其关联，一个代表一维。同样的，我们对第一维不感兴趣，因为它趋向于和每个标题词的数量有关系。

book 0.15 -0.27 0.04 dads 0.24 0.38 -0.09 dummies 0.13 -0.17 0.07 estate 0.18 0.19 0.45 guide 0.22 0.09 -0.46 investing 0.74 -0.21 0.21 market 0.18 -0.30 -0.28 real 0.18 0.19 0.45 rich 0.36 0.59 -0.34 stock 0.25 -0.42 -0.28 value 0.12 -0.14 0.23

*

3.91 0 0 0 2.61 0 0 0 2.00

*

T1 T2 T3 T4 T5 T6 T7 T8 T9 0.35 0.22 0.34 0.26 0.22 0.49 0.28 0.29 0.44 -0.32 -0.15 -0.46 -0.24 -0.14 0.55 0.07 -0.31 0.44 -0.41 0.14 -0.16 0.25 0.22 -0.51 0.55 0.00 0.34