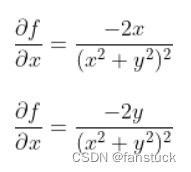一文速学数模-最优化算法(二)梯度下降算法一文详解+Python代码
目录
前言
一、梯度下降法简述
二、梯度下降算法原理理解
1.梯度
2.梯度定义
3.梯度下降
4.损失函数(loss function)
5.学习率(步长)
三、梯度下降算法代码展示
消失和爆炸梯度
前言
最近会不断更新深度学习系列文章(全实战性+可运行代码)加入到我的一文速学-数学建模常用模型中,现在建模比赛不用深度学习的知识和技能竞争力就比较落后了,况且我也任职人工智能开发工程师,对这一块的理论和实战都比较多。而且对于学习深度学习方面知识我也比较熟悉疑难点和重要知识点,故开此系列大家可以放心订阅,质量绝对有保证且内容易学易懂实践轻松,每个知识点都接有小段代码可供验证。
博主专注建模四年,参与过大大小小数十来次数学建模,理解各类模型原理以及每种模型的建模流程和各类题目分析方法。此专栏的目的就是为了让零基础快速使用各类数学模型、机器学习和深度学习以及代码,每一篇文章都包含实战项目以及可运行代码。博主紧跟各类数模比赛,每场数模竞赛博主都会将最新的思路和代码写进此专栏以及详细思路和完全代码。希望有需求的小伙伴不要错过笔者精心打造的专栏。
一、梯度下降法简述
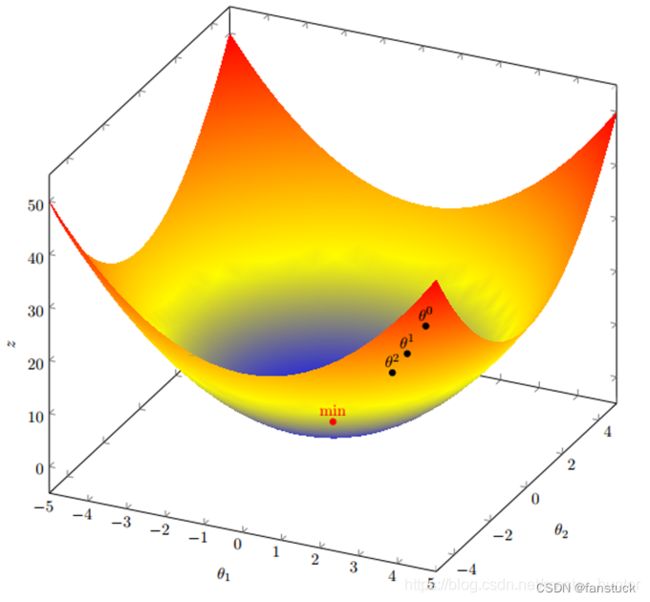
梯度下降算法(GradientDescent Optimization)是常用的最优化方法之一,“最优化方法”属于运筹学方法,是指在某些约束条件下,为某些变量选取哪些值,可以使得设定的目标函数达到最优问题。
梯度下降算法中的成本函数就像一个晴雨表,通过每次参数更新的迭代来衡量其准确性。 在函数接近或等于零之前,模型将持续调整其参数,以使产生的误差尽可能的小。一旦机器学习模型 的准确性得到优化,它们就可以成为人工智能 (AI) 和计算机科学应用的强大工具。
我之前没有单独拿出梯度上升算法来直接细讲但是讲了也非常的详细,之前提过一个例子不知道大家还是否有印象:
我们可以设想所得到的每一个解就是一登山者,我们希望这些登山者能够爬上高峰。所以求最大值的过程就转化成一个“爬山”的过程。
在梯度上升算法理解中我是这么写的:
我们总是往向着山顶的方向攀爬,当爬到一定角度以后也会驻足停留下观察自身角度是否是朝着山顶的角度上攀爬(从搜索空间中随机产生邻近的点,从中选择对应解最优的个体,替换原来的个体,不断重复上述过程。)。并且我们需要总是指向攀爬速度最快的方向爬。但是这座山不一定是最高峰,只能达到局部最优解而不是全局。
而梯度下降大家只需要把这个山倒过来就好了,成了下坡到谷底。
那么这里有几个我们需要知道的概念和理论。
二、梯度下降算法原理理解
既然是梯度下降那么我们肯定需要对梯度这个数理概念有个比较熟悉的理解。
1.梯度
梯度下降算法基于的思想是:要找到函数的最小值,最好的方法是沿着该函数的下降方向探寻。对此我们需要明白代表函数变化快慢的导数以及偏导数,在此基础上我们不仅要知道函数在坐标轴正方向上的变化率(即偏导数),而且还要设法求得函数在其他特定方向上的变化率。而方向导数就是函数在其他特定方向上的变化率。梯度与方向导数有一定的关联性,在微积分里面,对多元函数的参数求delta偏导数,把求得的各个参数的偏导数以向量的形式写出来,就是梯度。
纯数理化的知识可能比较难懂,我们可以结合实际例子来了解:一座高度在![]() 点是
点是![]() 的山。
的山。![]() 这一点的梯度是在该点坡度(或者说斜度)最陡的方向。梯度的大小告诉我们坡度到底有多陡。
这一点的梯度是在该点坡度(或者说斜度)最陡的方向。梯度的大小告诉我们坡度到底有多陡。
梯度也可以告诉我们一个数量在不是最快变化方向的其他方向的变化速度。再次结合山坡的例子。可以有条直接上山的路其坡度是最大的,则其坡度是梯度的大小。也可以有一条和上坡方向成一个角度的路,例如投影在水平面上的夹角为60°。则,若最陡的坡度是40%,这条路的坡度小一点,是20%,也就是40%乘以60°的余弦。
这个现象可以如下数学的表示。山的高度函数![]() 的梯度点积一个单位向量给出表面在该向量的方向上的斜率。这称为方向导数。
的梯度点积一个单位向量给出表面在该向量的方向上的斜率。这称为方向导数。
2.梯度定义
设二元函数![]() 在平面区域D上具有一阶连续偏导数,则对于每一个点P(x,y)都可定出一个向量,
在平面区域D上具有一阶连续偏导数,则对于每一个点P(x,y)都可定出一个向量, ,该函数就称为
,该函数就称为![]() 在点
在点![]() 的梯度,记作
的梯度,记作![]() 或
或![]() 。
。
那么我们现在对一个函数![]() 求它的梯度:
求它的梯度:
对其求偏导可知:
函数在某一点的梯度是这样一个向量,它的方向与取得最大方向导数的方向一致,而它的模为方向导数的最大值。
3.梯度下降
梯度下降算法的起点是我们评估性能的任意点。 在这个起点上,我们可以求出导数(或斜率),并可以用切线来观察斜率的大小。 斜率将引起参数的更新,即权重和偏差。 起始点处的斜率会更大,但随着新参数的生成,斜率会逐渐减小,直到达到曲线上的最低点,即收敛点。
与线性回归中寻找最佳拟合线类似,梯度下降算法的目标是使成本函数最小化,即最大程度减少预测值与实际值之间的误差。 为了做到这一点,需要两个数据点——一个是方向,另一个是学习速率。 这些因素决定了未来迭代的偏导数计算,使其逐渐达到局部或全局最小值(即收敛点)。
4.损失函数(loss function)
损失函数就是用以衡量实际值和预测值在当前位置的差值或误差。这提高了机器学习模型的有效性,通过向模型提供反馈,使其可以调整参数以最大程度减少误差,并找到局部或全局最小值。 成本函数会不断迭代,并沿着最陡下降(或负梯度)的方向移动,直到接近或等于零。到达此位置时,模型将停止学习。 损失函数根据不同的算法其也有很多不同的种类,这里暂时不展开细讲,后续会单独开一篇文章细讲所有传统的机器学习以及深度学习的一些常用损失函数。
5.学习率(步长)
学习率指的是为了达到最小值所采取的步长的大小。可以理解为下坡的跨度,这通常是一个很小的值,它会根据成本函数的行为进行评估和更新。较高的学习速率具有更大的步长,但也有错过最小值的风险。 相反,较低的学习速率的 步长较小。 虽然较低的学习速率具有更高精度的优势,但迭代的次数会降低整体效率,因为这个过程将需要更多的时间和计算来达到最小值。
三、梯度下降算法代码展示
本案例出自:《深度学习与图像识别:原理与实践》这本书,如果想要深入学习深度学习算法的同学推荐细读。
我们可以通过构建函数来进一步梯度下降算法:
import numpy as np
import matplotlib.pyplot as plt
if __name__ == '__main__':
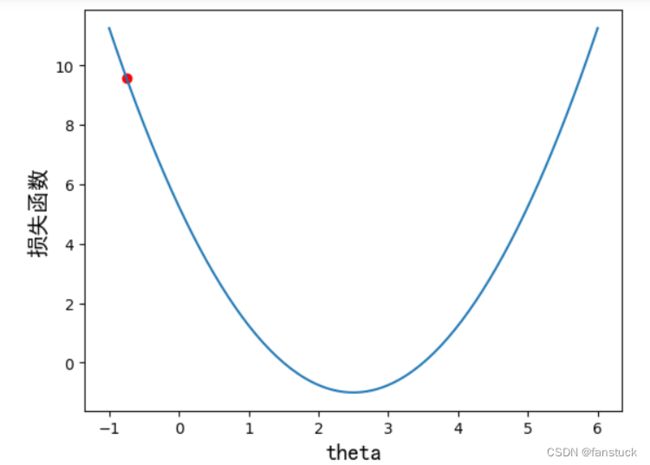
plot_x = np.linspace(-1,6,141)#从-1到6选取141个点
plot_y = (plot_x - 2.5)**2 -1 #二次方程的损失函数
plt.scatter(plot_x[5],plot_y[5],color='r') #设置起始点,颜色为红色
plt.plot(plot_x,plot_y)
#设置坐标轴名称
plt.xlabel('theta',fontproperties='simHei',fontsize=15)
plt.ylabel('损失函数',fontproperties='simHei',fontsize=15)
plt.show()上述代码画出损失函数示意图,x轴代表的是参数theta,y轴代表的是损失函数的值(即Loss值),曲线y代表的是损失函数。我们的目标是希望通过大量的数据训练和调整参数theta,使得损失函数的值最小,可以通过求导数的方式,达到二次方程的最小值点,使得导数为0即可。
梯度下降中有个比较重要的参数:学习率eta,它控制模型寻找最优解的速度。
首先定义损失函数以及导数:
def J(theta): #损失函数
return (theta-2.5)**2-1
def dJ(theta): #损失函数的导数
return 2*(theta-2.5)通过matplotlib绘制梯度下降迭代过程 :
theta = 0.0 #初始点
theta_history = [theta]
eta = 0.1 #步长
epsilon = 1e-8 #精度问题或者eta的设置无法使得倒数为0
while True:
gradient = dJ(theta)
last_theta = theta #先记录下上一个theta的值
theta = theta - eta * gradient #得到一个新的theta
theta_history.append(theta)
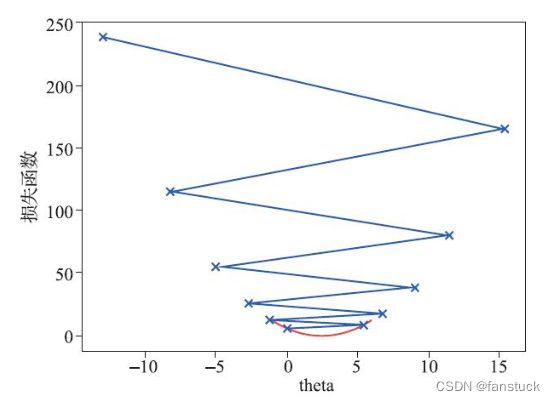
if(abs(J(theta)-J(last_theta))关于步长我们可以自行调整数值大小,进行比对,我们再设置为0.01和0.8再看:
第一个例子很明显学习的速度变慢了,第二个例子蓝色的步长在损失函数之间发生了跳跃,不过在跳跃的过程中,损失函数的值依然在不断地变小,步数是22步,因此学习率为0.8时,优化过程的时间缩短。
但是我们这里需要注意的是如果我们将步长调到1.1时:
过大的步长很可能导致模型不收敛。
消失和爆炸梯度
在更深层次的神经网络中,特别是在 递归神经网络中,当使用梯度下降算法和反向传播算法训练模型时,我们还会遇到另外两个问题。
- 消失梯度: 在梯度过小时发生。 当我们在反向传播过程中向后移动时,梯度将持续变得更小,导致网络中早期层的学习速度比后期层慢。 当这种情况发生时,权重参数会进行更新,直到它们变得微不足道——即等于零,这将导致算法不再学习。
- 爆炸梯度: 在梯度太大时会发生这种情况,会使创建的模型不稳定。 在这种情况下,模型权重会变得太大,并最终被表示为 NaN。 解决这个问题的一种方法是利用降维技术,这有助于最大程度地降低模型中的复杂性。