《剑指0ffer》:栈与队列经典题目分析
1.实现一个栈,要求实现Push(出栈)、Pop(入栈)、Min(返回最小值)的时间复杂度为O(1)
主要思路:
1)建立两个栈_data与_mindata,其中_data作为数据栈,存放每一个入栈的数据;_mindata作为数据最小栈,存放数据栈中当前最小的数据;
2)当元素data入栈时,将data入栈到_data数据栈中,并让data与_data的栈顶元素做比较,如果x小于等于_data的栈顶元素,则将data入栈到_mindata最小数据栈中;
3)当元素出栈时,让_data与_mindata的栈顶元素做比较,如果栈顶元素相等,则将_data与_mindata的栈顶元素同时出栈,否则只让_data数据栈的栈顶元素出栈;
4)当求栈中最小元素时,直接让最小元素栈的栈顶元素出栈。
#include
#include
using namespace std;
typelate
class Minstack
{
public:
void push(const T &data)
{
_data.push(data);
if(_mindata.empty() || data <= _mindata.top())
{
_mindata.push(data);
}
}
void pop()
{
if(_data.empty())
{
return;
}
if(!_data.empty() && _data.top() == _mindata.top())
{
_mindata.pop();
}
_data.pop();
}
const T Min()
{
if(_mindata.empty())
{
return T();
}
return _mindata.top();
}
void Print()
{
while(!_data.empty())
{
cout<<_data.top()<<" ";
_data.pop();
}
cout< _data, _mindata;
};
2.使用两个栈实现一个队列
思路: push 比较容易,直接把数据push 进stack1中
pop需要将stack1中的数据push进stack2中,这样栈1的先入后出就可以变成栈2的先入先出,将栈2中的顶部数据返回即为队列的pop数据
再将栈2中的数据push回去栈1,保持原始状态。
public class Solution
{
public:
Stack stack1 = new Stack();
Stack stack2 = new Stack();
//入栈给stack1
void push(int node)
{
stack1.push(node);
}
//pop
//出栈时,若stack2不为空,则出栈,
* 若为空,把stack1的内容全部放入stack2,然后出栈。
public int pop()
{
while(!stack2.isEmpty())
{
return stack2.pop();
}
while(!stack1.isEmpty())
{
return stack2.pop(stack1.pop);
}
return stack2.pop();
}
public static void main(String[] args)
{
}
};
3.使用两个队列实现一个栈
思路:
1.先设计两个队列:一个用于入栈input,一个用于出栈output
2.当元素要入栈的时候,直接入栈input
3.当元素要出栈时,先判断output中是否有元素。若是有,可以直接将output中的栈顶元素出队列;若是没有,则先将input中的元素入到output中,再判断栈是否为空,若不为空,将output的元素除队尾元素外入到input中,再将output中的栈顶元素出队列;
4.判断队列是否为空,依次判断input与output是否为空,若有其中一个栈不为空,则队列就不为空;
5.求栈顶元素,首先判断栈是否为空,若不为空,将input中的元素入到output中,若output不为空,则打印output队尾元素;
6.求队列的大小,将队列input与output的大小相加即可。
#include
template
class Two_Queue_To_Stack
{
public:
//插入
void Push(const T& x)
{
input.push(x);
}
//删除
void Pop()
{
if(!output.empty())
{
output.pop();
}
else
{
while(!input.empty())
{
output.push(input.front());
input.pop();
}
if(!Empty())
{
while(output.size() - 1)
{
input.push(output.front());
output.pop();
}
output.pop();
}
else
{
cout<<"删除时发现该队列为空"< input;
queue output;
};
void TestTwo_Queue_To_Stack()
{
Two_Queue_To_Stack q;
q.Push(1);
q.Push(2);
q.Push(3);
q.Push(4);
q.Push(5);
//q.Printf();
q.Pop();
q.Pop();
q.Pop();
//q.Pop();
//q.Pop();
//q.Pop();
//q.Printf();
cout<<"Empty: "<
4.元素出栈、入栈顺序的合法性。如入栈的序列(1,2,3,4,5),出栈序列为 (5,4,3,2,1)
这道题我们可以创建两个栈(感觉有点类似两个栈实现一个队列),需要几个数字放在前面即把S1的栈顶元素取几个放在S2里面即可
![]()
出栈时候先判断S2是否为空,不为空则从S2栈顶元素逐个取出,再从S1中取出剩下的元素即可
#include
#include
#include
using namespace std;
typlate int T
class Stack
{
public:
Stack()
{}
~Stack()
{}
//push
void push(T data)
{
s1.push(data);
}
//pop
void pop()
{
while(!s2.empty())
{
cout<<"s2.pop"<<"s2.top"<<")"< s1.size() && x<0)
return ;
while(x)
{
T temp = s1.top();
if(!s1.empty())
{
s1.pop();
s2.push(temp);
}
--x;
}
}
private:
stack s1;
stack s2;
};
int main()
{
Stack s;
s.Push(1);
s.Push(2);
s.Push(3);
s.Push(4);
s.Push(5);
s.NumReverse(2);
s.Pop();
s.Pop();
s.Pop();
s.Pop();
return 0;
}
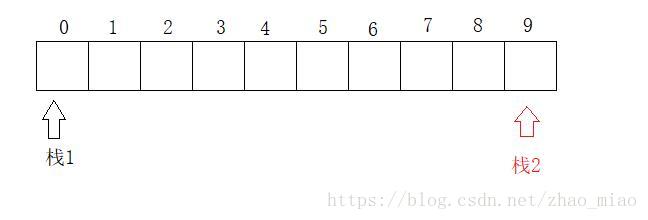
5.一个数组实现两个栈(共享栈)
方法:
下标为0的位置为栈1的栈底,栈2的栈底在下标最大的位置上。栈1向左扩展,栈2向后扩展。这种方法不会出现浪费内存的情况。
#define Max 10
#define DataType int
typedef struct SharedStack
{
DataType data[Max];
int top1;
int top2;
}sharedstack;栈的初始化:
//共享栈初始化
void InitShared(sharedstack *s)
{
assert(s);
s->top1 = 0;
s->top2 = Max - 1;
memset(s->data, 0, Max*sizeof(DataType));
}入栈:
//while == 1 表示栈1,d表示要入栈的数据
void PushSharedStack(sharedstack *s, DataType d, int which)
{
assert(s);
if(while == 1)
{
if(s->top1 <= s->top2)
{
s->data[s->top1++] = d;
}
else
{
printf("栈满\n");
return;
}
}
else
{
if(s->top1 <= s->top2)
{
s->data[s->top2--] = d;
}
else
{
printf("栈满\n");
return;
}
}
}出栈:
void PopSharedStack(sharedstack *s, int which)
{
assert(s);
if(while == 1)
{
if(s->top1 != 0)
{
s->top1--;
}
else
{
printf("栈空\n");
return ;
}
}
else
{
if(s->top2 != 0)
{
s->top2++;
}
else
{
printf("栈空\n");
return;
}
}
}栈顶元素:
DataType SharedStackTop(sharedstack *s, int which)
{
assert(s);
if(while == 1)
{
if(s->top1 == 0)
{
printf("栈空\n");
return -1;
}
else
{
return s->data[s->top1-1];
}
}
else
{
if(s->top2 == 0)
{
printf("栈空\n");
return -1;
}
else
{
return s->data[s->top2+1];
}
}
}栈长短:
//栈长短
DataType SharedStackSize(sharedstack *s, int which)
{
assert(s);
if (which == 1)
{
return s->top1;
}
else
return Max - s->top2 - 1;
}***6.滑动窗口的最大值
给定一个数组和滑动窗口的大小,找出所有滑动窗口里数值的最大值。例如,如果输入数组{2,3,4,2,6,2,5,1}及滑动窗口的大小3,那么一共存在6个滑动窗口,他们的最大值分别为{4,4,6,6,6,5}; 针对数组{2,3,4,2,6,2,5,1}的滑动窗口有以下6个: {[2,3,4],2,6,2,5,1}, {2,[3,4,2],6,2,5,1}, {2,3,[4,2,6],2,5,1}, {2,3,4,[2,6,2],5,1}, {2,3,4,2,[6,2,5],1}, {2,3,4,2,6,[2,5,1]}。
/*时间复杂度o(n),空间复杂度为o(n)
思路就是采用双端队列,队列中的头节点保存的数据比后面的要大。
比如当前假如的数据比队尾的数字大,说明当前这个数字最起码在从现在起到后面的过程中可能是最大值
,而之前队尾的数字不可能最大了,所以要删除队尾元素。
此外,还要判断队头的元素是否超过size长度,由于存储的是下标,所以可以计算得到;
特别说明,我们在双端队列中保存的数字是传入的向量的下标;
*/
class Solution {
public:
vector maxInWindows(const vector& num, unsigned int size)
{
vector vec;
if(num.size()<=0 || num.size() dq;
//处理前size个数据,因为这个时候不需要输出最大值;
for(unsigned int i=0;i=num[dq.back()])
dq.pop_back();//弹出比当前小的元素下标
dq.push_back(i);//队尾压入当前下标
}
//处理size往后的元素,这时候需要输出滑动窗口的最大值
for(unsigned int i=size;i=num[dq.back()])
dq.pop_back();
if(!dq.empty() && dq.front()<=(int)(i-size))//判断队头的下标是否超出size大小,如果超过,要删除队头元素
dq.pop_front();//删除队头元素
dq.push_back(i);//将当前下标压入队尾,因为可能在未来是最大值
}
vec.push_back(num[dq.front()]);//最后还要压入一次
return vec;
}
};