《剑指offer》:线性表经典题目分析
1、逆置单链表
typedef struct LinkNode
{
int val;
LinkNode*next;
};
//单链表逆置
void Reverse(ListNode* pHead)
{
if(pHead == NULL || pHead->next == NULL)
{
return;
}
LinkNode*Recv = NULL;
//p指针指向头结点
LinkNOde*pCur= head;
while( p != NULL)
{
ListNode* pTemp = pCur;
pCur = pCur->next;
pTemp->next = Recv;
Recv = pTemp;
}
return Recv;
}初始状态:
![]()
第一次循环:
![]()
第一次循环过后,步骤①:pTemp指向Head,步骤②:pCur指向P1,步骤③:pTemp->pNext指向NULL
此时得到的pRev为:
![]()
第二次循环:
![]()
第二次循环过后,步骤①:pTemp指向P1,步骤②:pCur指向P2,步骤③:pTemp->pNext指向Head
此时得到的pRev为:
![]()
第三次循环:
![]()
第三次循环过后:步骤①:pTemp指向P2,步骤②:pCur指向P3,步骤③:pTemp->pNext指向P1。
此时得到的pRev为:
![]()
第四次循环:
![]()
第四次循环过后:步骤①:pTemp指向P3,步骤②:pCur指向NULL,步骤③:pTemp->pNext指向P2
此时得到的pRev为:
![]()
全部完成
2、反转单链表
/*
#inlucde
using namespace std;
class LinkNode
{
public:class LinkNode
{
int val;
Linknode *next;
LinkNode (int val)
{
this.val = val;
}
}
};
*/
//反转链表
public class Solution
{
public ListNode ReverseList(ListNode head)
{
if(head == NULL)
return ;
LinkNode pre =NULL;
LinkNode next = NULL;
while(head !=NULL)
{
next = head.next;
head.next = pre;
pre = head;
head = next;
}
return pre;
}
};
/*
//反转链表
public ListNode ReverseList1(ListNode head) {
if (head == null)
return null; // head为当前节点,如果当前节点为空的话,那就什么也不做,直接返回null;
ListNode pre = null;
ListNode next = null;
// 当前节点是head,pre为当前节点的前一节点,next为当前节点的下一节点
// 需要pre和next的目的是让当前节点从pre->head->next1->next2变成pre<-head next1->next2
// 即pre让节点可以反转所指方向,但反转之后如果不用next节点保存next1节点的话,此单链表就此断开了
// 所以需要用到pre和next两个节点
// 1->2->3->4->5
// 1<-2<-3->4->5
while(head != null){ //注意这个地方的写法,如果写head.next将会丢失最后一个节点
// 做循环,如果当前节点不为空的话,始终执行此循环,此循环的目的就是让当前节点从指向next到指向pre
// 如此就可以做到反转链表的效果
// 先用next保存head的下一个节点的信息,保证单链表不会因为失去head节点的原next节点而就此断裂
next = head.next; //先让head.next指向的节点,即第二个节点叫next
head.next = pre; //将head.next指向pre,也就是说断开head节点与后面的连接
pre = head;//pre,head依次向后移动一个节点,进行下一次反转
head = next;
}
// 如果head为null的时候,pre就为最后一个节点了,但是链表已经反转完毕,pre就是反转后链表的第一个节点
return pre;
}
//合并两个递增的链表并且保证最终的链表也是单调不减的。
3、合并两个有序的单链表
//递归的方式
/*
public ListNode Merge(ListNode list1,ListNode list2)
{
if (list1 == null)
{
return list2;
}
if (list2 == null)
{
return list1;
}
ListNode newHead = null;
if (list1.val <= list2.val)
{
newHead = list1;
newHead.next = Merge(list1.next,list2);
}
else
{
newHead = list2;
newHead.next = Merge(list1,list2.next);
}
return newHead;
}
*/
4、判断单链表是否有环?环的入口点?环的长度?
问题1:
首先要判断一个链表是否带环,我们可以分别考虑一下带环和不带环两种情况的区别。如果链表不带环,我们用一个指针从头遍历到尾
指针最终会指向一个NULL 。如果链表带环指针一旦进入环就会一直循环遍历,这样就会陷入死循环永远走不到 NULL位置。
这时我们可以考虑用两个指针去遍历整个链表,分别为fast和slow,fast一次走两步,slow一次走一步,如果链表不带换那么fast或者
fast->next就会走到 NULL,如果链表带环,fast和slow就会在环的某一个节点相遇,这样我们就能很快判断出链表是否带环了。
代码如下(判断链表是否带环):
ListNode* IsExitsLoop(ListNode* pHead)
{
if(pHead == NULL || pHead->next == NULL || pHead->next->next == NULL)
{
return ;
}
ListNode* slow = pHead->next;//走一步
LinkNode* fast = pHead->next->next;//走两步
while(slow != fast)
{
if(fast == NULL || fast->next == NULL)
{
cout<<"没有环"<next;
fast = fast->next;
}
cout<<"有环"< 问题2:
如果该链表已经证明带环,那么环的入口地址在哪里?我们用下图来详细说明一下。上一步我们通过slow和fast相遇得出链表带环,如图所示
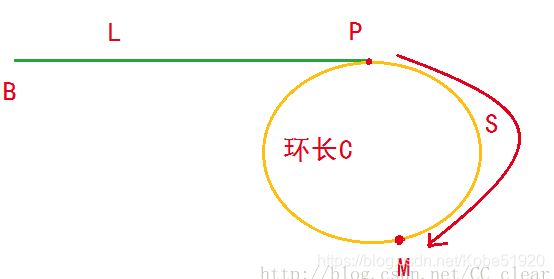
假设相遇在M点,设环的入口位置为点P,链表头结点为B,从B到P我们假设长度为L,从P到M长度记为S,整个环长度为C。我们分析一下fast和slow从出发到相遇一共走了多长?
对于fast:因为相遇之前可能在环内循环了n圈所以总路程为 L+nC+S
对于slow:总路程为 L+S
由于slow每次走一步,fast每次走两步。因此就有了 L+nC+S = 2(L+S) 解方程得到:L = nC - S 。这个等式什么意义?M点现在是fast和slow相遇的位置
我们可以记录这个位置,让一个cur从链表头B出发每次走一步,slow指针继续从相遇的点出发每次一步,当cur走了L长后到了环入口P,此时slow指针到哪里呢?
我们分析一下,slow之前已经从P点走了S长,从解方程的结果可以得出S = nC-L , 此时给slow再走L长即 S+L 就神奇的到了环的入口。
所以当cur和slow相遇的地方就是环的入口。
ListNode* IsExitsLoop(ListNode* pHead)
{
if(pHead == NULL || pHead->next == NULL || pHead->next->next == NULL)
return NULL;
ListNode* slow = pHead->next,*fast = pHead->next->next;
while(slow!=fast)
{
if(fast == NULL || fast->next == NULL)
return NULL;
slow = slow->next;
fast = fast->next->next;
}
slow = pHead;
if(slow != fast)
{
slow = slow->next;
fast = fast->next;
}
return slow;
}问题3:环的长度
已经知道了环的入口位置,我们让一个指针从环入口出发,当再次走到该位置时走过的长度就是环的长度了
int LoopPortLength(ListNode* pPort)
{
ListNode *pCur = pPort;
int length = 1;
if(pCur != pPort)
{
pCur = pCur->next;
length++;
}
return length;
}
5、判断两个单链表是否相交?交点?
**思路:
**求第一个交点:两个指针p1 p2 先求出两个单链表的长度之差 pos ,使p1指向较长的单链表头节点,然后p1向前走pos,p2指向较短的单链表,从头开始遍历,当p1 = p2,则相交且为两个相交的单链表的第一个交点
void LinkListpoint(linklist *p1, linklist *p2)
{
int count = 0 ;//相差的
int count1 = 0;//p1
int count2 = 0;//p2
Linklist*Cur1 = p1;
Linklist*Cur2 = p2;
//p1的长度
while (cur1 != NULL)
{
count1++;
cur1 = cur1->next;
}
//p2的长度
while (cur2 != NULL)
{
count2++;
cur2 = cur2->next;
}
cur1 = p1;
cur2 = p2;
//p1与p2的差
count = count1 - count2;
if(count >= 0)
{
while(count--)
{
cur1 = cur1->next;
}
while(cur1 != cur2)
{
cur1 = cur1->next;
cur2 = cur2->next;
}
printf("%d\n",cur1->data);
}
else
{
while (count--)
{
cur2 = cur2->next;
}
while (cur1 != cur2)
{
cur1 = cur1->next;
cur2 = cur2->next;
}
printf("%d\n", cur2->data);
}
}
6、O(1)时间删除单链表的一个节点
**思路:
要删除节点 i,先把 i 的下一个节点 j 的内容复制到 i,然后把 i 的指针指向节点 j 的下一个节点,此时再删除j节点,其效果刚好是把节点i删除了,如果要删除的节点位于链表的尾部,要从链表的头节点开始,顺序遍历得到该节点的前序节点,并完成删除操作如果链表中只有一个节点,并要删除链表的头节点(也是尾节点),删除后,要将链表的头节点设置为NULL
public:
ListNode deleteNode(ListNode head, ListNode deleteNode)
{
if(head == NULL || deleteNode == NULL)
{
return NULL;
}
if(deleteNode -> next != NULL)
{
listNode * next = deleteNode->next;
deleteNode -> val = next->val;
deleteNode -> next = next ->next;
}
else
{
//当这个结点是尾结点
if(deleteNode->next == NULL)
{
return NULL;
}
//删除的节点是多节点的尾节点
else
{
ListNode *cur = head;
while(cur->next !=deleteNode)
{
cur = cur->next;
}
cur.next = null;
}
}
return head;
}
7、最快时间内找到单链表倒数第K个节点?
思路:
设置两个指针p1和p2,p1向前走k-1步后,p1和p2同时向前遍历,当p1走向尾节点时,p所在位置即倒数第k个节点
Node *LastK(List plist,int k)
{
if(plist == NULL ||k == NULL)
{
return NULL;
}
LinkNode *p1=plist;
LinkNode *p2=plist;
while(k-1>0)
{
if(p1->next != NULL)
{
p1 = p1->next;
--k;
}
else
{
return NULL;
}
}
while(p1->next != NULL)
{
p1 = p1->next;
p2 = p2->next;
}
return p2;
}
8、最快时间内删除单链表倒数第K个节点?
void DeleteLastK(List plist,int k)
{
if(k < 0 || plist == NULL)
{
return ;
}
Node *p1 = plist;
Node *p2 = plist;
while(k > 0)
{
if(p1->next != NULL)
{
p1 = p1->next;
--k;
}
else
{
return;
}
}
while(p1->next != NULL)
{
p1 = p1->next;
p2 = p2->next;
}
Node *pDel = p2->next;
p2->next = pDel->next;
free(pDel);
pDel = NULL;
}
9、 求两个顺序表的交集、并集和差集
1.交集:
新开辟一个顺序表存放交集,如果遍历两个顺序表,查找相同元素写入交集中,并记录长度
void Intersection(PSqlist sq1,PSqlist sq2,PSqlist sq3)
{
int k = 0;
for(int i = 0;i < sq1->length ;i++ )
{
while(j < sq2->length && sq2->elem[j] != sq1->elem[i])
{
j++;
}
}
if(jlength)
{
sq3->elem[k++] = sq2->elem[j];
}
sq3->length = k;
}
2.并集:
思路(并集):
新开辟一个顺序表存放并集,由于是并集,所以结果中至少包含了一个顺序表中的所有元素,因此首先将第一个顺序表写入并集。然后遍历第二个顺序表,每拿到一个元素都遍历一遍第一个顺序表,进行比对,第一个顺序表遍历完毕, 第二个顺序表中的该元素在第一个顺序表中依然没有找到与之相等的元素,就将第二个顺序表中的该元素就写入并集
void Uoion(psalmist sq1,psalmist sq2,psalmist sq4)
{
//第一条链表的全部数据都要入新的链表中
for(int i = 0;i < sq1->length ;i++)
{
sq4->elem[i] = sq1->elem[i];
}
sq4->length = sq1->length;
int k = sql->length;
//遍历第一条链表与第二条链表中数据做对比
for(int i = 0;i < sq2->length ;i++)
{
int j = 0;
while(j < sq1->length && sq1->elem[j] != sq2->elem[i] )
{
j++;
}
if(j == sq1->length)
{
sq4->elem[k++] = sq2->elem[i];
}
}
sq4->length = k;
}3.差集:
新开辟一个顺序表存放差集,属于A而不属于B的元素的集合称为A与B的差,则遍历第一个顺序表,每拿到一个元素都遍历一遍第二个顺序表,进行比对,第二个顺序表遍历完毕,第一个顺序表中的该元素在第二个顺序表中依然没有找到与之相等的元素,就将第一个顺序表中的该元素写入差集。
void Difference_Set (PSqlist sq1,PSqlist sq2,PSqlist sq5)
{
int k = 0;
for (int i = 0; i < sq1->length; i++)
{
int j = 0;
while(j < sq2->length && sq1->elem[i] != sq2->elem[j])
{
j++;
}
if (j == sq2->length)
{
sq5->elem[k++] = sq1->elem[i];
}
}
sq5->length = k;
}
10、求两个有序单链表的交集、并集和差集
两个有序的无头结点的链表La,Lb,求二者的交集、并集、差集,并且把结果分别存在一个新链表中返回。
1.交集:
依次遍历两个链表,比较两个链表当前元素的大小关系
如果两个链表当前元素相等,则找到一个相交元素
如果第一个链表元素小于第二个链表元素,则第一个链表的指针后移一位
如果第一个链表元素大于第二个链表元素,则第二个链表的指针后移一位
BNode *Intersection(BTlist plist1,BTlist plist2)
{
BTlist Lc;
Lc = NULL; // 初始化无头单链表
BTlist p1 = plist1;
BTlist p2 = plist2;
BTlist p3 = Lc;
while(p1 != NULL && p2!= NULL)
{
if(p1->data < p2->data)
{
p1 = p1->next;
}
else if
{
p2= p2->next;
}
else//插入新链表中
{
//申请空间
BNode *pGet = (BNode *)malloc(sizeof(BNode));
pGet->next = NULL;
pGet->data = p2->data;
if (p3 == NULL)
{
Lc = pGet; // 第一个交集元素节点存入Lc
p3 = Lc;
}
else
{
while (p3->next != NULL)
{
p3 = p3->next;
}
p3->next = pGet;
}
//Insert_tail(&Lc,p2->data);
p1 = p1->next;
p2 = p2->next;
}
}
return Lc;
}2.并集:
依次遍历两个链表,比较两个链表当前元素的大小关系
** 如果第一个链表元素小于第二个链表元素,则第一个链表当前元素存入新链表,并后移第一个链表指针
** 如果第一个链表元素大于第二个链表元素,则第二个链表当前元素存入新链表,并后移第二个链表指针
** 如果第一个链表元素等于第二个链表元素,则第一个链表当前元素存入新链表,并后移第一个和第二个链表指针
** 如果两个链表中某个还有剩余,则将剩余元素插入新链表
BNode *Union(BTlist plist1,BTlist plist2)
{
BTlist Lc
Lc = NULL;
BTlist p1= plist1;
BTlist p2= plist2;
PTlist p3= Lc
while( p1 != NULL && p2 != NULL)
{
if(p1->data < p2->data)
{
Insert_tail(&Lc,p1->data);
p1 = p1->next;
}
else if
{
Insert_tail(&Lc,p2->data);
p2 =p2->next;
}
else
{
Insert_tail(&Lc,p1->data);
p1 = p1->next;
p2 = p2->next;
}
}
while (p1 != NULL)
{
Insert_tail(&Lc,p1->data);
p1 = p1->next;
}
while (p2 != NULL)
{
Insert_tail(&Lc,p2->data);
p2 = p2->next;
}
return Lc;
}3.差集:
依次遍历两个链表,比较两个链表当前元素的大小关系
** 如果两个链表当前元素相等,则两个链表的指针均后移一位
** 如果第一个链表元素小于第二个链表元素,则第一个链表的元素肯定是独有的,所有加入到结果链表中
** 如果第一个链表元素大于第二个链表元素,则第二个链表的指针后移一位
BNode *Difference_Set(BTlist plist1,BTlist plist2)
{
BTlist Lc;
Lc = NULL; // 初始化无头单链表
BTlist p1 = plist1;
BTlist p2 = plist2;
while(p1 != NULL && p2 != NULL)
{
if (p1->data < p2->data)
{
Insert_tail(&Lc,p1->data);
p1 = p1->next;
}
else if(p1->data > p2->data)
{
p2 = p2->next;
}
else
{
p1 = p1->next;
p2 = p2->next;
}
}
while (p1 != NULL)
{
Insert_tail(&Lc,p1->data);
p1 = p1->next;
}
return Lc;
}
11、求两个单链表(可以无序)的交集、并集和差集
先创建一个单链表:
bool IsPresent(BTlist plist,int elem)
{
BTlist p = plist;
while(p != NULL)
{
if(p->data == elem)
{
return true;
}
}
p= p->next;
}交集:
依次遍历第一个链表,在第二个链表中查找该元素
如果第二个链表中也有该元素,则将该元素插入到结果链表中。
BNode *Intersection_1(BTlist plist1,BTlist plist2)
{
BTlist Lc;
Lc = NULL; // 初始化无头单链表
BTlist p1 = plist1;
BTlist p2 = plist2;
while(p1 != NULL)
{
if (IsPresent(p2,p1->data))
{
Insert_tail(&Lc,p1->data);
}
p1 = p1->next;
}
return Lc;
}
并集:
现将第一个链表全部插入结果链表中
** 然后遍历第二个链表,若第二个链表中的某元素在结果链表中不存在
** 则将该元素插入到结果链表中。
BNode *Union_1(BTlist plist1,BTlist plist2)
{
BTlist Lc;
Lc = NULL; // 初始化无头单链表
BTlist p1 = plist1;
BTlist p2 = plist2;
while(p1 != NULL)
{
Insert_tail(&Lc,p1->data);
p1 = p1->next;
}
while(p2 != NULL)
{
if(!IsPresent(Lc,p2->data))
{
Insert_tail(&Lc,p2->data);
}
p2 = p2->next;
}
return Lc;
}
差集:
遍历第一个链表,若该元素在第二个链表中不存在,则将该元素插入到结果链表中
BNode *Difference_Set_1(BTlist plist1,BTlist plist2)
{
BTlist Lc;
Lc = NULL; // 初始化无头单链表
BTlist p1 = plist1;
BTlist p2 = plist2;
while(p1 != NULL)
{
if(!IsPresent(p2,p1->data))
{
//尾插法
Insert_tail(&Lc,p1->data)
}
p1 = p1->next;
}
return Lc;
}