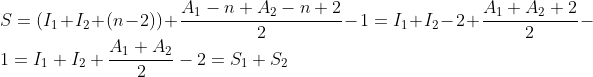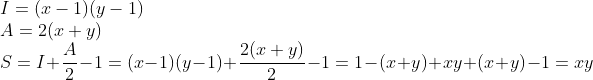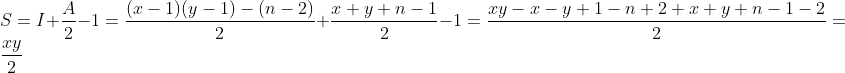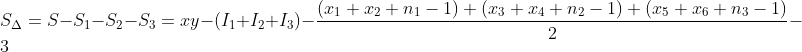图论之毕克定理证明
毕克定理是小学四年级奥赛内容,无意间从一本教材上看到,觉得定理蛮有意思,也和自己从事的工作有一些关联,就在网上找了一些证明资料,结合自己的思考,稍微挖掘了以下,聊以记录。
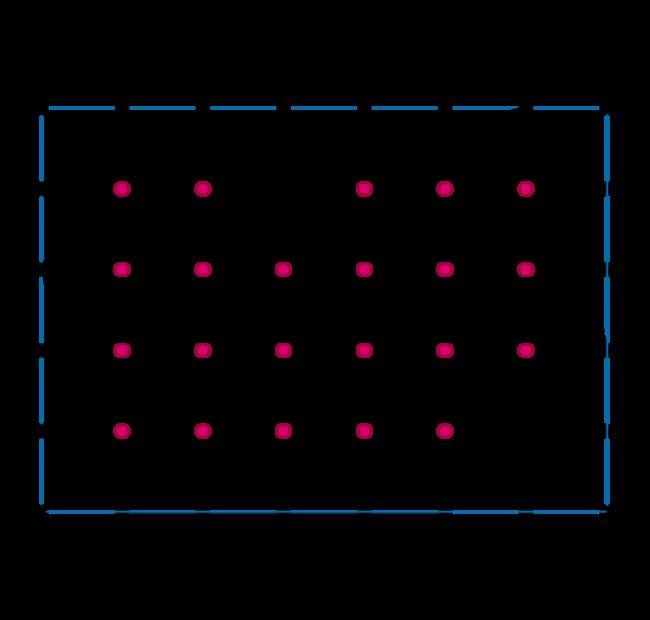
毕克定理是指一个计算点阵中顶点在格点上的多边形面积公式,该公式可以表示为S=N+L÷2-1,其中N表示多边形内部的点数,L表示多边形落在格点边界上的点数,S表示多边形的面积。
公式默认一个小正方形边长为1,即面积为1,若一个格点正方形边长为2(面积为4)时,需要在原有公式的基础上乘4.
1.定理大概描述:
给定一个网格,每个格子由边长为1的单位正方形组成。网格内有一个多边形,并且多边形的顶点都在网格的交点处,也就是说顶点没有一个落在了单位正方形的边上或者单位正方形的内部,记多边形的面积为S,多边形内部的点的个数为I,多边形边上的点数为A,则:
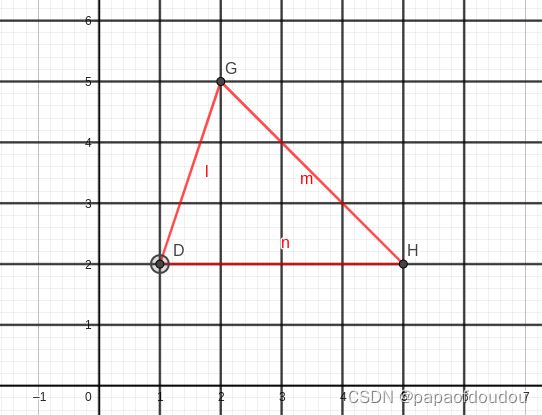
证明,以下图为例,红色的点是内点,分布在边缘线条上的点是边点。
首先用割补,将其补充为一个矩形,假设矩形面积为S,边缘三角形的面积分别如图所示,则不规则多边形面积为:
![]()
1、证明步骤
(1)首先,证明对长方形是成立的;
(2)接着,再证明对直角三角形是成立的;
(3)然后,继续证明对任意三角形也是成立的;
(4)最后,证明对于两个图形的组合还是成立的。
首先证明(4)
假设任意一个多边形的面积都有:
对多边形1来说:
对多边形2来说:
如果多边形1和2共享一条边,这个边有n个边点,则按照公式,由1和2组合拼成的图形为:
得证。
其次证明对长方形是成立的:
长方形的长、宽长度分别为x,y.
成立。
关于A的计算方式,可以参考欧拉定理,面数F=1, 所以定点数等于线段数。举行的定点数等于线段数。
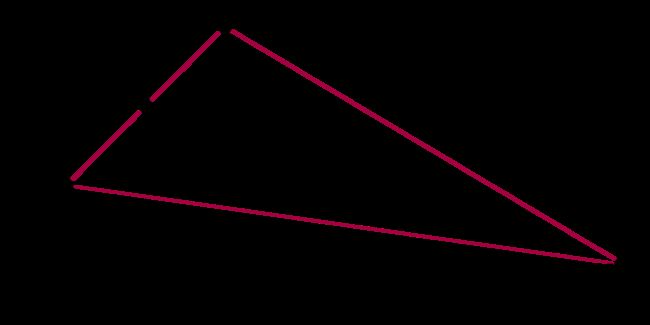
对于三角形同样成立,先看直接三角形,将红色的直角三角形补为矩形:
假设对角线穿过的点为n.则对于红色三角形来说:
![]()
则:
成立。
对于任意三角形可以由 1个长方形 = 若干直角三角形 + 此三角形拼接而成,用上面拆解的方法同理可证。
![]() 为长度,
为长度,![]() 为三角形三个边经过的点的个数,
为三角形三个边经过的点的个数,![]() 为三个直角三角形的内点个数,则:
为三个直角三角形的内点个数,则:
![]()
![]()
分别用几何法和毕克定力求不规则三角形面积:
几何法:
毕克定理法:
接下来化简几何法:
因为:
所以:
可以看到,两种方法,最终都化成了形式:
所以,命题得到证明,不规则三角形同样适用毕克定理。
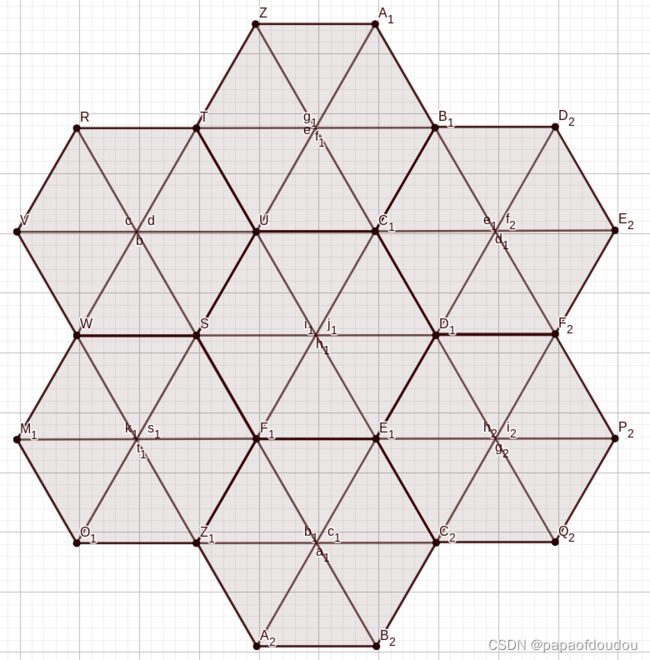
在毕克定理中,又分为棱形网格和三角形网格,我们下面证明对棱形网络也成立。
证明棱形网络符合毕克定理
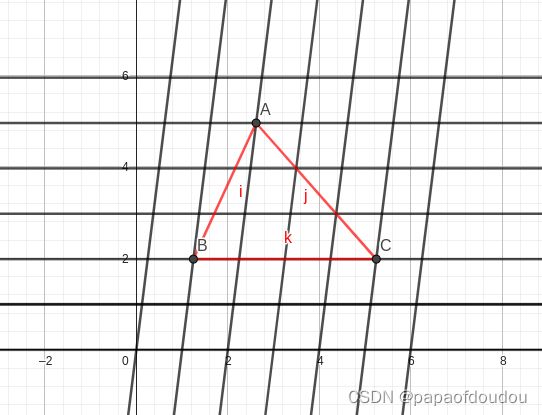
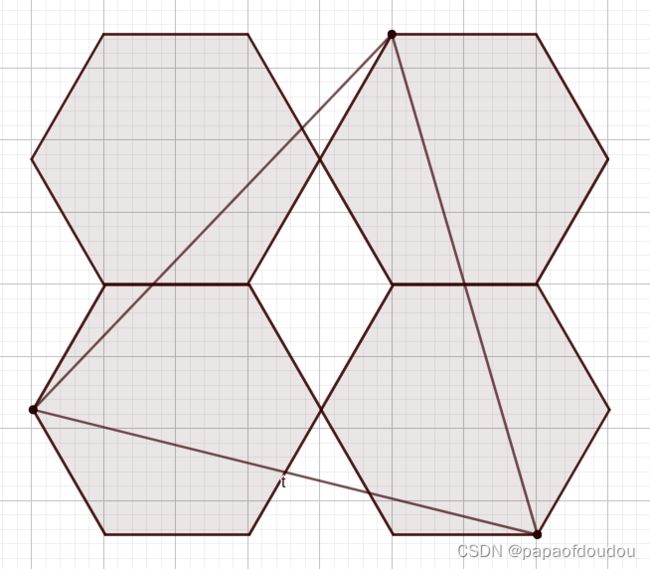
初等几何我们知道,四边形不是稳定的形状,四边形是可以通过固定一边,平移另一边来变化面积和和形状。在线性代数中,这种变化叫做线性变换,因为它没有改变平行和0点不动的性质。我们可以考虑对下图进行这种变换:
你会看到,一个三角形,在经过这种变换后,仍然是个三角形,并且他的内点,外点和边缘点的数量和相对位置没有任何变化,只是图形面积同比例的缩小。对比如下三角形,在变换前后,内点和边缘点的数量没有任何变化。
由于是线性变换,任何一部分的面积都以相同的比例缩小,所以以小棱形计的格点多边形仍然满足毕克定理,这是线性变换的自然推论。
所以,对于棱形组成的网格,也可以应用毕克定理。
对于三角形成立
为了方便,以等边三角形为例(任意三角形都可以,其实等边三角形没有对证明带来额外信息,只是方便画图)。
前面证明了任意三角形符合毕克定理,而基于任意三角形之上添加新的边,组成新的形状,每一步也都证明了符合毕克定理,所以无论由三角形组成的面多么复杂,最终的图形也都会符合毕克定理,证明结束。
或者用前面的结论,两个正三角形组成一个棱形,符合毕克定理,而且棱形分解成正三角形,没有带来额外的内点和外点的变化,只是最小面积单元从棱形变为了原来的一半,正三角形的面积。
所以如果以正三角形计,相对于原来棱形的公式,最后结果要乘以2。棱形面积是正三角形的2倍。
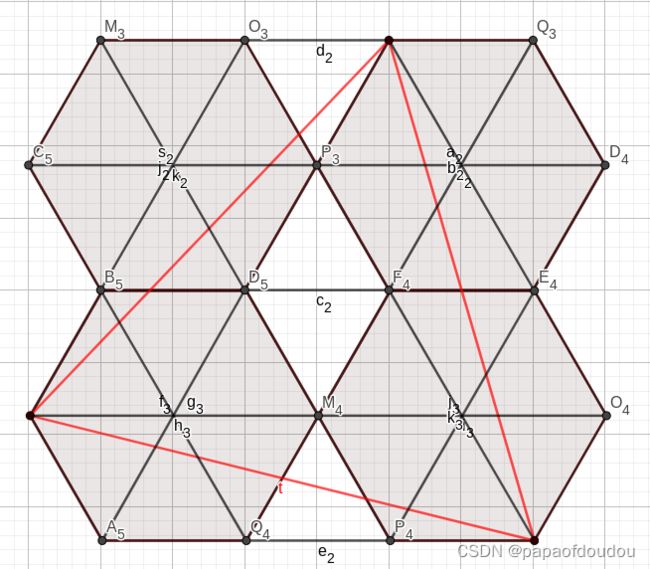
证明完成后,看下图求大的三角形面积,是不是就很简单了?
只要将图形分解成棱形或者正三角形,应用毕克定理即可解决这个问题,不赘述。
思考:
由于任何不规则图形都可以分解成三角形和矩形,矩形也可以进一步分解成三角形,所以其实这个问题只要考虑三角形即可。所以,实际上只要证明前面的结论3和4,便可证明毕克定理。
联想:
实际上,由于任何不规则图形都可以分解成三角形,矩形这个条件可以变的更弱一些,我们只需要证明毕克定理适用于不规则三角形以及结论4即可推导出毕克定理的普适性结论。因为联想到GPU的设计,任何图元都可以分解为三角形平面的组合。所以自然所有的格点几何图形也都适用于毕克定理这个结论。
二维空间中最简单的面就是三角形面,GPU的流水线在顶点处理和光栅化阶段,就是将几何图元分解成一个一个的三角形处理的,并且PIPELINE算法也会针对三角形进行特殊优化。
![]()
无论多么复杂的几何形状,都可以看成无限多个微小三角形拼接而成的。
参考资料
「图形基础」笔记2. 图形处理单元GPU_gpu画图为什么都是三角形形状_周婕的博客-CSDN博客