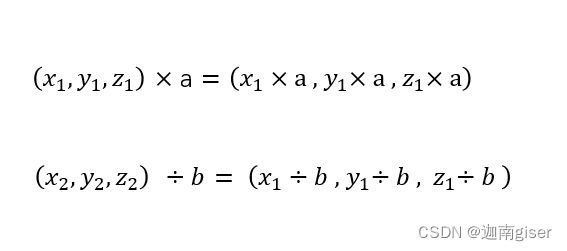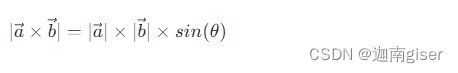webgl——必须掌握的数学知识

---

前言

想要学好WebGL，良好的数学储备是必不可少的，本节详细地介绍与WebGL相关的数学知识，并总结这些知识在图形学中的应用。

---

坐标系

屏幕坐标系

屏幕坐标系一般是 X 轴向右，Y 轴向下

右手、左手坐标系

右手坐标系与左手坐标系是常用的空间坐标系，WebGL默认遵从右手坐标系的规则

其它坐标系

webgl完整的坐标转换流程共经过六个坐标系，有些坐标对于开发者是无感的，但是有利于开发者加深对图形学的理解，参照 webgl坐标转换

• 1.物体（模型）坐标系
• 2.世界坐标系
• 3.观察坐标系
• 4.裁剪坐标系
• 5.规范化设备坐标系
• 6.屏幕坐标系

向量

向量是既有大小，又有方向的量，在物理中又称为矢量

向量一般用一个上方带箭头的字母表示，高中数学知识告诉我们，矢量在坐标系中即可以表示一个向量，也可以表示一个顶点坐标。在WebGL中，如果一个 vec4类型向量（x，y，z，w）中的 w 分量不为0，那么它代表的必然是一个点坐标。

向量比较

因为向量既有大小又有方向，所以两个向量相等有两层意思：方向相同，大小相同，所以判断两个向量是否相等，可以通过它们在各个坐标轴上的分量是否相等来判断。

在GLSL中内置了很多矢量比较的函数：

名称	类型	含义
lessThan(vec1, vec2)	bvec2/bvec3/bvec4	逐分量比较vec1 < vec2 是否成立
lessThanEqual(vec1, vec2)	bvec2/bvec3/bvec4	逐分量比较vec1 <= vec2 是否成立
greaterThan(vec1, vec2)	bvec2/bvec3/bvec4	逐分量比较vec1 > vec2 是否成立
greaterThanEqual(vec1, vec2)	bvec2/bvec3/bvec4	逐分量比较vec1 >= vec2 是否成立
equal(vec1, vec2)	bvec2/bvec3/bvec4	逐分量比较vec1 = vec2 是否成立
notEqual(vec1, vec2)	bvec2/bvec3/bvec4	逐分量比较vec1 != vec2 是否成立

向量大小、单位向量

• 向量大小

三维空间某向量（x，y，z）的模（大小）为

• 单位向量

单位向量是 长度为1 的向量，一般对于向量来讲，我们有一个统一的大小标准，这个标准就是单位向量，在这个标准下，我们只需要关心向量的方向。比如入射光线、反射光线等，如果不对向量进行归一化，光线就会过于明亮或者黑暗。

将向量（x，y，z）转化为单位向量的过程我们称之为归一化向量，计算方式为

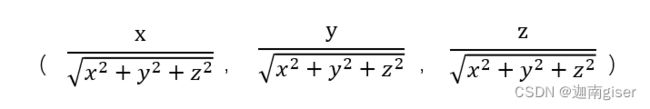
在GLSL中提供有现成的归一化函数 normalize

名称	类型	含义
normalize(v)	float/vec	向量归一化为单位向量

行向量和列向量

向量可以看成一个特殊的矩阵，尤其在顶点着色器中，点的坐标向量都被当作一个矩阵来进行运算

一个点坐标为（x，y，z，w）的向量可以表示为一个 4 行 1 列的列矩阵，或者一个 1 行 4 列的行矩阵。行向量和列向量的具体介绍可参考后续矩阵介绍。

着色器中vec[i]类型的数据都是在乘号的右侧，由此推断他们在webgl都是列向量（4 X 1 矩阵）方式进行矩阵运算的

向量基本运算：向量加减、向量与标量乘除

• 加减

维度相同的两个向量才可以相减，新向量各个分量为原向量各个分量之和或差。

• 向量不能和标量相加。
• 向量加法满足交换律

• 向量与标量乘除

向量和标量不能进行加减操作，只能进行乘除操作，向量和标量乘除后返回一个新向量，新向量的各个分量等于原向量的各个分量和标量的积或商

向量重要运算：点乘与叉乘

向量之间可以相乘，向量之间乘法包含点乘和叉乘两种

• 点乘

向量点乘的数学意义是将两个向量的各个分量的乘积相加，返回一个标量

向量点乘的几何意义是两个向量的模相乘然后再乘以夹角的余弦

向量点积在WebGL中的应用相当广泛，比如在计算光照时,就运用到了向量的点乘，参考webgl——给场景添加光，根据点积运算结果还能判断目标是位于前方还是后方。

<漫反射光颜色> = <入射光颜色> × <表面基底色> × cos θ
= <入射光颜色> × <表面基底色> × ( <光线方向> * <法线方向>)

在GLSL中提供有现成的点积函数 dot，在大多数情况下，进行运算前都要先对向量进行归一化。

名称	类型	含义
dot(x,y)	float	返回x和y之间的内积/点乘

• 叉乘

两个向量叉乘结果是一个新向量，新向量的方向垂直于原来两个向量所在的平面，z轴指向通过右手定则来判定。

向量叉乘的数学算法如下

新向量的大小等于两个向量模的乘积再乘以向量夹角的正弦值，即向量组成的平行四边形的面积。

在GLSL中同样提供有现成的叉积函数 cross。

名称	类型	含义
cross(x,y)	vec	返回x和y之间的外积/叉乘

矩阵

矩阵是按照行列排列的一系列数值的集合，由 m × n 个数排成的m行n列的数表称为m行n列的矩阵，简称m × n 矩阵，如下图。当 m 和 n 相同则称这个方阵为 m 阶矩阵(方阵)。

矩阵加减

应该注意的是只有同维度矩阵之间才可以进行加减，即为行数和列数都必须一样的两个矩阵才可以进行加减运算。矩阵加减运算的规则是将两个矩阵对应位置上的元素相加减：

矩阵数乘

矩阵和标量相乘，返回一个新矩阵，新矩阵的各个元素等于原矩阵各个元素与标量的乘积：

矩阵乘矩阵

两个矩阵的乘法仅当第一个矩阵A的列数和另一个矩阵B的行数相等时才能进行义。如A是m×n矩阵和B是n×p矩阵，它们的乘积C是一个m×p矩阵，规则如下：

矩阵相乘满足分配律和结合律，但不满足交换律：

由于矩阵乘法不满足交换律，所以两矩阵相乘时要说明是左乘还是右乘，一般来讲矩阵 A 和矩阵 B 相乘指的是A左乘B，即 A X B，A 右乘 B 即 B X A。

矩阵转置

把矩阵A的行和列互相交换所产生的矩阵称为A的转置矩阵$$A^T$$

逆矩阵

设A是一个n阶矩阵，若存在另一个n阶矩阵B，使得： AB=BA=E ，则称方阵A可逆，并称方阵B是A的逆矩阵，单位矩阵是一个对角线上的元素都为1的方阵，其余元素为 0，比如下面就是一个 3 阶单位矩阵：

• 不是所有的矩阵都存在逆矩阵，逆矩阵首先必须是方阵，而且存在与其相乘结果为单位矩阵的矩阵
• 在图形学中，将进行矩阵变换的坐标再乘以该变换矩阵的逆矩阵，可以将变换后的坐标再还原回去，实现撤销的效果

正交矩阵

假设有一个方阵M，当且仅当 M 与其转置矩阵M^T的乘积等于单位矩阵时，称其为正交矩阵。即：

即：

此时方阵M为一个正交矩阵，矩阵正交需要满足以下两个条件：

• 矩阵的每一行都是单位向量
• 矩阵的某一行和其他行向量相互垂直，点积为 0

两个向量a = [a1, a2,…, an]和b = [b1, b2,…, bn]的点积定义为：a·b=a1*b1 + a2*b2 + … + an*bn

行主序和列主序

在JavaScript中，没有专门用来表示矩阵的类型，需要使用类型化数组 new Float32Array 来存储，但是数组是一维的，矩阵是二维的，将二维的矩阵存储到一维数组中有两个方式：行主序和列主序。

webgl按照列主序的规则将矩阵存储于数组，对于上面这个矩阵，按照列主序存到数组中一个是这样的：

 new Float32Array([ a,  e,  i,  m, b,  f,  j,  n,  c,  g,  k,  o, d,  h,  l,  p,]) 

一般在程序中这样书写，看起来更加舒服

new Float32Array([
    a,  e,  i,  m,
    b,  f,  j,  n,
    c,  g,  k,  o,
    d,  h,  l,  p,
   ]) 

WebGL 中的投影矩阵

• 正射投影矩阵

已知 上平面t 、 下平面b、近平面n、远平面f、左平面l、右平面r：

• 透视投影矩阵

已知摄像机 视角α 、 宽高比aspect、近平面n、远平面f：

其它数学知识

三角函数

glsl内置三角函数，内容很基础，不再一 一详细介绍

名称	类型	含义
sin()	float / vec	弧度的正弦值
cos()	float / vec	弧度的余弦值
tan()	float / vec	弧度的正切值
asin()	float / vec	反正弦值
acos()	float / vec	反余弦值
atan()	float / vec	反正切值

基本数学运算

如指数函数、幂函数等等，可参考OpenGL ES着色器语言——内置函数。