超简单!!!搭建阿克曼ROS小车
超简单!!!搭建阿克曼ROS小车
0、前言
本篇文章仅是对常见阿克曼ROS小车的极简分析,并提供代码。主要是方便读者自己搭建阿克曼小车时理解使用。
这里仅针对《舵机控制前轮转向+后轮主动差速》的方式,如下图所示:
图片来源:百度图片
舵机转向机构简单示意图
舵机完成前轮的转向控制,简单示意图如下:
图片来源:Pinterest
1、整体设计
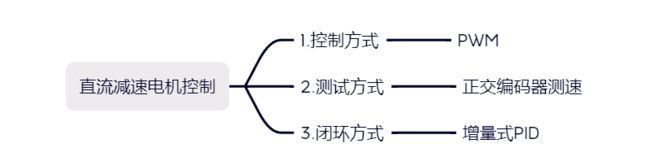
若要能实现阿克曼小车的搭建,需要明确小车的控制方式和控制数据的层级关系;如下图所示:
2、STM32底层控制部分
2.1、后轮差速控制
后轮电机差速控制和差速小车的控制方式一样,都是采用光电\霍尔编码器测速+PID闭环控制的方式,如下图所示,这里就不赘述了。
需要了解的朋友可以看之前的文章,链接如下:
2.2、前轮舵机角度控制
2.2.1、舵机选型:
这里主要使用如下两种模拟舵机,常见模拟舵机都可以。
图片来源:百度图片
2.2.2、舵机控制原理:
舵机是一种位置伺服驱动器,是一种带有输出轴的小装置。当我们向伺服器发送一个控制信号时,输出轴就可以转到特定的位置。只要在控制信号持续不变,伺服机构就会保持相对的角度位置不变。如果控制信号发生变化,输出轴的位置也会相应发生变化。舵机的控制大部分都是通过PWM信号控制的。
2.2.3、单片机控制舵机:
模拟舵机控制一般需要20ms左右时基脉冲, 该脉冲高电平部分一般为0.5ms-2.5ms范围内角度控制脉冲部分, 总间隔为2ms。 以180度角度伺服为例, 对应控制关系如下 :
控制示意图如下:
图片来源:ArduinoGetSarted.com
2.2.4、阿克曼小车舵机控制代码:
主函数初始化:
Steer_PWM_Init(60000-1, 24-1); //=====初始化PWM 50HZ,用于驱动舵机
PWM配置部分代码(STM32):
/**************************************************************************
函数功能:控制转向舵机的PWM初始化
入口参数:无 PB0 -> TIM1
返回 值:无
**************************************************************************/
void Steer_PWM_Init(u16 arr,u16 psc)
{
GPIO_InitTypeDef GPIO_InitStructure;
TIM_TimeBaseInitTypeDef TIM_TimeBaseStructure;
TIM_OCInitTypeDef TIM_OCInitStructure;
RCC_APB2PeriphClockCmd(RCC_APB2Periph_GPIOB | RCC_APB2Periph_AFIO, ENABLE);
RCC_APB2PeriphClockCmd(RCC_APB2Periph_TIM1, ENABLE);
GPIO_PinRemapConfig(GPIO_PartialRemap_TIM1, ENABLE);
GPIO_InitStructure.GPIO_Pin = GPIO_Pin_0;
GPIO_InitStructure.GPIO_Mode = GPIO_Mode_AF_PP;
GPIO_InitStructure.GPIO_Speed = GPIO_Speed_50MHz;
GPIO_Init(GPIOB, &GPIO_InitStructure);
TIM_TimeBaseStructure.TIM_Period = arr;
TIM_TimeBaseStructure.TIM_Prescaler = psc;
TIM_TimeBaseStructure.TIM_ClockDivision = TIM_CKD_DIV1;
TIM_TimeBaseStructure.TIM_CounterMode = TIM_CounterMode_Up;
TIM_TimeBaseInit(TIM1, &TIM_TimeBaseStructure);
TIM_OCInitStructure.TIM_OCMode = TIM_OCMode_PWM1;
// * TIM1_CH2
// TIM_OCInitStructure.TIM_OutputState = TIM_OutputState_Enable;
// TIM_OCInitStructure.TIM_Pulse = 0;
// TIM_OCInitStructure.TIM_OCPolarity = TIM_OCPolarity_High;
// * TIM1_CH2N
TIM_OCInitStructure.TIM_OutputNState = TIM_OutputNState_Enable;
TIM_OCInitStructure.TIM_Pulse = 0;
TIM_OCInitStructure.TIM_OCNPolarity = TIM_OCNPolarity_Low;
TIM_OC2Init(TIM1, &TIM_OCInitStructure); //TIM_OC2
TIM_OC2PreloadConfig(TIM1, TIM_OCPreload_Enable);
TIM_ARRPreloadConfig(TIM1, ENABLE); //使能TIMx在ARR上的预装载寄存器
TIM_CtrlPWMOutputs(TIM1, ENABLE); //MOE 主输出使能 高级定时器使用
TIM_Cmd(TIM1, ENABLE);
}
前轮转向控制角度和PWM的转换函数:
//舵机PWM变量,初始安装为90度,注意机械安装时,要先转到90度再安装舵盘
int motorFrontSteer = 4500; // (60000 / 20ms) * 1.5ms = 4500 90度
//舵机控制角度的设定值
int frontAngleSet = 0;
// 物理结构限幅,舵机角度限幅
#define MAX_FRONT_ANGLE_SET (50)
/**************************************************************************
函数功能:舵机角度控制处理(SG90)角度线性变化
入口参数:ros端设定转向角度,需要给舵机的pwm,此处可根据不同的舵机自行更改
分辨率:1度 --> ((2.5ms - 0.5ms) / 180度) * (60000 / 20ms) = 33.3
0.5ms ------------------ 0度
1.5ms ------------------ 90度
2.5ms ------------------ 180度
返回 值:无
**************************************************************************/
void Steer_Ctrl(int frontAngleSet,int *motorFrontSteer)
{
// 物理结构限幅
if(frontAngleSet > MAX_FRONT_ANGLE_SET)
{
frontAngleSet = MAX_FRONT_ANGLE_SET;
}
if(frontAngleSet < -MAX_FRONT_ANGLE_SET)
{
frontAngleSet = -MAX_FRONT_ANGLE_SET;
}
// 正常计算角度
if(frontAngleSet == 0) //默认初始角度 90度
{
*motorFrontSteer = 4500; // (60000 / 20ms) * 1.5ms = 4500
}
else if(frontAngleSet > 0) // left
{
*motorFrontSteer = 4500 - (int)(myabs(frontAngleSet) * 33.3 + 0.5);
}
else //right
{
*motorFrontSteer = 4500 + (int)(myabs(frontAngleSet) * 33.3 + 0.5);
}
}
通过上面转换函数 Steer_Ctrl,我们可以将前轮转向角度转换为具体的PWM数值,剩下的部分就是PWM设置的问题了,大家这么聪明,肯定不用我多说了。
大家是不是觉得阿克曼小车的底层控制部分 So Easy.
3、极简版阿克曼结构运动学模型
3.1、模型示意图介绍:
阿克曼底盘的运动学模型是一个全驱动模型,简化模型示意图如下:
图片来源:CSDN:Jason.Li_0012
3.2、模型假设:
相对于理想的阿克曼底盘模型,这里为了简化模型,做了如下假设:
- 不考虑车辆在Z轴方向的运动,只考虑XY水平面的运动。
- 左右侧车轮转角一致,这样可将左右侧轮胎合并为一个轮胎,以便于搭建单车模型。
- 车辆行驶速度变化缓慢,忽略前后轴载荷的转移。
3.3、模型已知条件:
- 小车前后轴之间的距离: l l l
- 小车后轮之间的距离:$ 2d$
- 小车前轮的转向角度: θ \theta θ
- 小车左侧后轮线速度: v L v_{L} vL
- 小车右侧后轮线速度: v R v_{R} vR
- 小车线速度: v v v
- 小车角速度: w w w
3.4、阿克曼小车后轮正逆运动学模型:
之前讲差速小车运动学模型的文章中,已经明确:差分模型的机器人始终做的是以R为半径的圆弧运动,这里阿克曼也可以安装同样的方式计算。
v = w ∗ R (公式 1 ) v=w*R (公式1) v=w∗R(公式1)
V L = w ∗ ( R − d ) = w ∗ R − w d = v − w d (公式 2 ) V_{L} = w * (R-d)=w*R - wd = v -wd (公式2) VL=w∗(R−d)=w∗R−wd=v−wd(公式2)
V R = w ∗ ( R + d ) = w ∗ R + w d = v + w d (公式 3 ) V_{R} = w * (R+d)=w*R + wd = v +wd (公式3) VR=w∗(R+d)=w∗R+wd=v+wd(公式3)
由 (公式 1 ) (公式1) (公式1)、 (公式 2 ) (公式2) (公式2)、 (公式 3 ) (公式3) (公式3)推导得到如下结果:
v = ( V L + V R ) / 2 (公式 4 ) v = (V_{L} + V_{R} )/ 2 (公式4) v=(VL+VR)/2(公式4)
w = ( V R − V L ) / 2 d (公式 5 ) w = (V_{R} - V_{L})/ 2d (公式5) w=(VR−VL)/2d(公式5)
3.5、阿克曼小车前轮转向角度计算:
这里使用两前轮中间的角度 θ \theta θ 来近似控制角,所以得到如下公式:
l / R = t a n θ (公式 6 ) l/R = tan\theta (公式6) l/R=tanθ(公式6)
R = v / w (公式 7 ) R=v/w(公式7) R=v/w(公式7)
由 (公式 6 ) (公式6) (公式6)、 (公式 7 ) (公式7) (公式7) 推导得到如下公式:
θ = a r c t a n ( l ∗ w / v ) (公式 8 ) \theta = arctan(l*w/v)(公式8) θ=arctan(l∗w/v)(公式8)
3.6、ROS层阿克曼模型计算代码分享:
#define PI (3.1415926)
#define ROBOT_RADIUS (0.0675) //m
#define ROBOT_TRACK (0.135) //m
#define ROBOT_LENGTH (0.15) //m
double RobotV_ = 0;
double YawRate_ = 0;
// 速度控制消息的回调函数
void cmdCallback(const geometry_msgs::Twist& msg)
{
RobotV_ = msg.linear.x; //m/s
YawRate_ = msg.angular.z; //rad/s
}
void Mbot::ackerCar(const double RobotV,const double YawRate)
{
double r = RobotV / YawRate; // m
if(RobotV == 0) // ackermann car can't trun rotation
{
sendLeftSpeed_ = 0;
sendRightSpeed_ = 0;
sendFrontAngle_ = 0;
}
else
if(YawRate == 0) // Pure forward/backward motion
{
sendLeftSpeed_ = (short)(RobotV * 1000.0);//mm/s
sendRightSpeed_ = (short)(RobotV * 1000.0);
sendFrontAngle_ = 0;
}
else // Rotation about a point in space
{
sendLeftSpeed_ = (short)(YawRate * 1000.0 * (r - ROBOT_RADIUS));//mm/s
sendRightSpeed_ = (short)(YawRate * 1000.0 * (r + ROBOT_RADIUS));
// 阿克曼约束一:后左右车轮转动需同向
if(RobotV > 0)
{
if(sendLeftSpeed_ < 0) {sendLeftSpeed_ = 0;}
if(sendRightSpeed_ < 0) {sendRightSpeed_ = 0;}
}
else if(RobotV < 0)
{
if(sendLeftSpeed_ > 0) {sendLeftSpeed_ = 0;}
if(sendRightSpeed_ > 0) {sendRightSpeed_ = 0;}
}
sendFrontAngle_ = atan(ROBOT_LENGTH * YawRate / RobotV ) * (180.0 / PI); // Deg
}
}
4、总结
如果你已经仔细的看到这里,那么恭喜你,你心中一定有了搭建阿克曼小车的控制思路了。
如果还没有理解,一定多看两遍。
偷偷的告诉大家,近期,我准备开源一整套,完整的ROS小车方案,包含差速小车和阿克曼小车,届时将给大家提供完整上位机和下位机的代码,整套方案成本极低,千元以内。
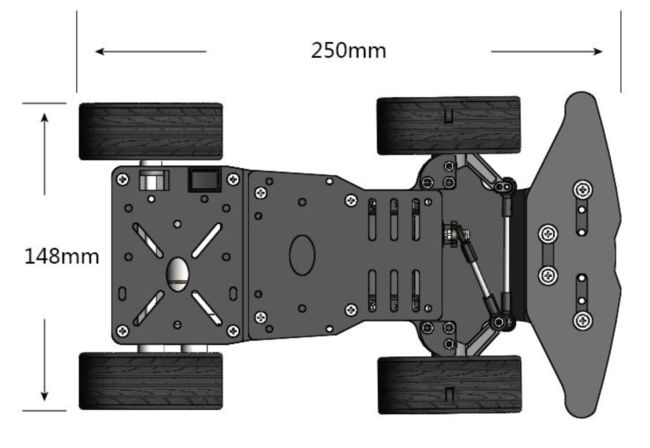
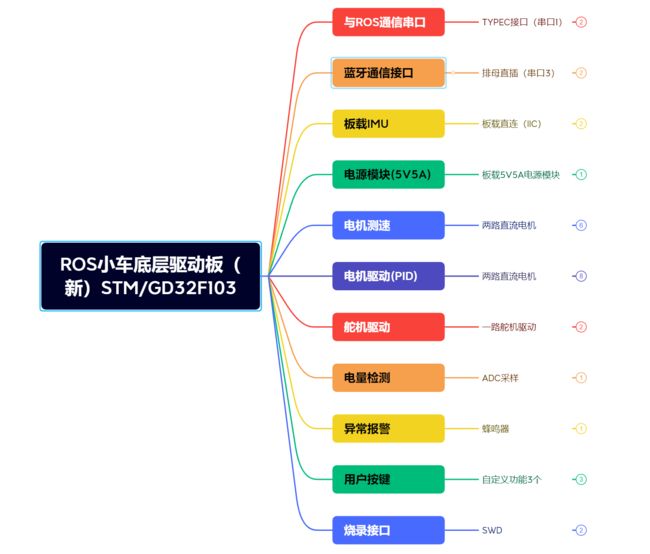
下面是底层硬件方案,提前透露给大家。
此处省略一点点细节…
全套方案开源:开源! ROS2阿克曼开发平台方案
5、参考:
[1] https://zhuanlan.zhihu.com/p/499251426
[2] https://blog.csdn.net/weixin_45929038/article/details/122632369?spm=1001.2014.3001.5502
[3] https://blog.csdn.net/weixin_47012067/article/details/121090584