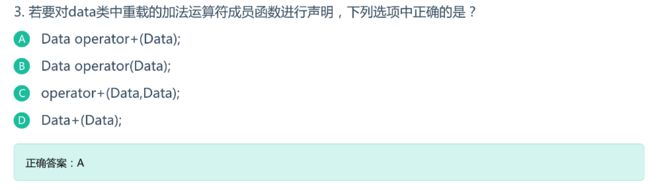
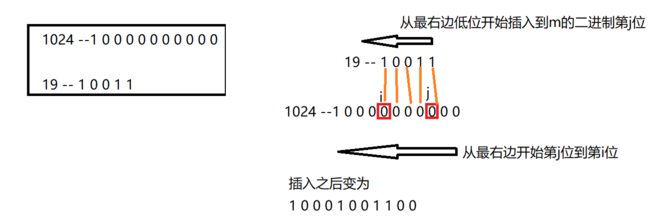
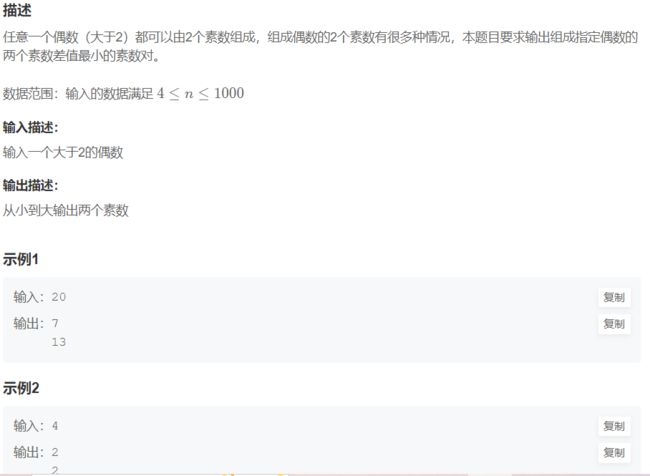
- c++ 的iostream 和 c++的stdio的区别和联系
黄卷青灯77
c++算法开发语言iostreamstdio
在C++中,iostream和C语言的stdio.h都是用于处理输入输出的库,但它们在设计、用法和功能上有许多不同。以下是两者的区别和联系:区别1.编程风格iostream(C++风格):C++标准库中的输入输出流类库,支持面向对象的输入输出操作。典型用法是cin(输入)和cout(输出),使用>操作符来处理数据。更加类型安全,支持用户自定义类型的输入输出。#includeintmain(){in
- 【JS】执行时长(100分) |思路参考+代码解析(C++)
l939035548
JS算法数据结构c++
题目为了充分发挥GPU算力,需要尽可能多的将任务交给GPU执行,现在有一个任务数组,数组元素表示在这1秒内新增的任务个数且每秒都有新增任务。假设GPU最多一次执行n个任务,一次执行耗时1秒,在保证GPU不空闲情况下,最少需要多长时间执行完成。题目输入第一个参数为GPU一次最多执行的任务个数,取值范围[1,10000]第二个参数为任务数组长度,取值范围[1,10000]第三个参数为任务数组,数字范围
- 2022-11-17
无奇君
又去了一次社康,这次是急性支气管炎……太难了。半夜就猛咳,天天咳醒,还好他戴海绵耳塞睡吵不到他,要不然对他来说也是种煎熬。一累也会猛咳,希望这次是最后一次吃药,吃完就好。又想把头发剪短了,顺便染个色。可是刚刚去看人家还没开门,不是休息日老板好佛系。理发店是个夫妻店,一年多前刚搬来的时候老板还没对象呢,当时聊天老板就说希望能找个对象一起两个人守着店都比上班强。不久后再去他已经有对象了,而且在店里帮忙
- 心有蓝天白云,爱情便会晴空万里,然后有花香有鸟鸣有美好的未来
曹十二吖
丁南的婚姻,来自于一场她对生命的对比。她曾经说过,当她最爱的母亲用生命去逼迫她结婚的时候,她曾一度不理解到愤怒,甚至于想过用轻生来对抗母亲的不理智。庆幸的是,丁南是一个自我调节能力非常强的人,她想如果我连死亡都不怕,还怕不能经营好一段婚姻吗?抱着这样的念头,24年没有谈过恋爱的她,用短短三个月的时间,完成了少女到女人的蜕变。她曾经说过:“我要把自己最珍贵的东西留给自己命中注定的那个人。”闺蜜几人中
- 基于CODESYS的多轴运动控制程序框架:逻辑与运动控制分离,快速开发灵活操作
GPJnCrbBdl
python开发语言
基于codesys开发的多轴运动控制程序框架,将逻辑与运动控制分离,将单轴控制封装成功能块,对该功能块的操作包含了所有的单轴控制(归零、点动、相对定位、绝对定位、设置当前位置、伺服模式切换等等)。程序框架由主程序按照状态调用分归零模式、手动模式、自动模式、故障模式,程序状态的跳转都已完成,只需要根据不同的工艺要求完成所需的动作即可。变量的声明、地址的规划都严格按照C++的标准定义,能帮助开发者快速
- C++ | Leetcode C++题解之第409题最长回文串
Ddddddd_158
经验分享C++Leetcode题解
题目:题解:classSolution{public:intlongestPalindrome(strings){unordered_mapcount;intans=0;for(charc:s)++count[c];for(autop:count){intv=p.second;ans+=v/2*2;if(v%2==1andans%2==0)++ans;}returnans;}};
- C++菜鸟教程 - 从入门到精通 第二节
DreamByte
c++
一.上节课的补充(数据类型)1.前言继上节课,我们主要讲解了输入,输出和运算符,我们现在来补充一下数据类型的知识上节课遗漏了这个知识点,非常的抱歉顺便说一下,博主要上高中了,更新会慢,2-4周更新一次对了,正好赶上中秋节,小编跟大家说一句:中秋节快乐!2.int类型上节课,我们其实只用了int类型int类型,是整数类型,它们存贮的是整数,不能存小数(浮点数)定义变量的方式很简单inta;//定义一
- 提高教师信息素养,提高道德与法治课教学效益
长白159宋彦红
提高教师信息素养,提高道德与法治课教学效益随着经济和社会的发展,信息技术已经运用到课堂教学中,为课堂教学展示了一个崭新的天地。的确,信息技术形象、生动、直观性强,能够将课本中的一些抽想的概念直接展示在学生面前,从而调动学生的眼、耳、脑,让他们兴奋起来,变被动学习为主动学习,充分发挥教师的教育引导作用,创造一个可以使学生积极参与的场景。在制作、使用信息技术的实践过程中,本文拟就教师提升信息素养的必要
- 母亲节如何做小红书营销
美橙传媒
小红书的一举一动引起了外界的高度关注。通过爆款笔记和流行话题,我们可以看到“干货”类型的内容在小红书中偏向实用的生活经验共享和生活指南非常受欢迎。根据运营社的分析,这种现象是由小红书用户心智和内容社区背后机制共同决定的。首先,小红书将使用“强搜索”逻辑为用户提供特定的“搜索场景”。在“我必须这样生活”中,大量使用了满足小红书站用户喜好和需求的内容。内容社区自制的高质量内容也吸引了寻找营销新途径的品
- Java面试题精选:消息队列(二)
芒果不是芒
Java面试题精选javakafka
一、Kafka的特性1.消息持久化:消息存储在磁盘,所以消息不会丢失2.高吞吐量:可以轻松实现单机百万级别的并发3.扩展性:扩展性强,还是动态扩展4.多客户端支持:支持多种语言(Java、C、C++、GO、)5.KafkaStreams(一个天生的流处理):在双十一或者销售大屏就会用到这种流处理。使用KafkaStreams可以快速的把销售额统计出来6.安全机制:Kafka进行生产或者消费的时候会
- 2024.9.6 Python,华为笔试题总结,字符串格式化,字符串操作,广度优先搜索解决公司组织绩效互评问题,无向图
RaidenQ
python华为leetcode算法力扣广度优先无向图
1.字符串格式化name="Alice"age=30formatted_string="Name:{},Age:{}".format(name,age)print(formatted_string)或者name="Alice"age=30formatted_string=f"Name:{name},Age:{age}"print(formatted_string)2.网络健康检查第一行有两个整数m
- 2019考研 | 西交大软件工程
笔者阿蓉
本科背景:某北京211学校电子信息工程互联网开发工作两年录取结果:全日制软件工程学院分数:初试350+复试笔试80+面试85+总排名:100+从五月份开始脱产学习,我主要说一下专业课和复试还有我对非全的一些看法。【数学100+】张宇,张宇,张宇。跟着张宇学习,入门视频刷一遍,真题刷两遍,错题刷三遍。书刷N多遍。从视频开始学习,是最快的学习方法。5-7月份把主要是数学学好,8-9月份开始给自己每个周
- C++ lambda闭包消除类成员变量
barbyQAQ
c++c++java算法
原文链接:https://blog.csdn.net/qq_51470638/article/details/142151502一、背景在面向对象编程时,常常要添加类成员变量。然而类成员一旦多了之后,也会带来干扰。拿到一个类,一看成员变量好几十个,就问你怕不怕?二、解决思路可以借助函数式编程思想,来消除一些不必要的类成员变量。三、实例举个例子:classClassA{public:...intfu
- 2021 CCF 非专业级别软件能力认证第一轮(CSP-J1)入门级C++语言试题 (第三大题:完善程序 代码)
mmz1207
c++csp
最近有一段时间没更新了,在准备CSP考试,请大家见谅。(1)有n个人围成一个圈,依次标号0到n-1。从0号开始,依次0,1,0,1...交替报数,报到一的人离开,直至圈中剩最后一个人。求最后剩下的人的编号。#includeusingnamespacestd;intf[1000010];intmain(){intn;cin>>n;inti=0,cnt=0,p=0;while(cnt#includeu
- 《 C++ 修炼全景指南:九 》打破编程瓶颈!掌握二叉搜索树的高效实现与技巧
Lenyiin
C++修炼全景指南技术指南c++算法stl
摘要本文详细探讨了二叉搜索树(BinarySearchTree,BST)的核心概念和技术细节,包括插入、查找、删除、遍历等基本操作,并结合实际代码演示了如何实现这些功能。文章深入分析了二叉搜索树的性能优势及其时间复杂度,同时介绍了前驱、后继的查找方法等高级功能。通过自定义实现的二叉搜索树类,读者能够掌握其实际应用,此外,文章还建议进一步扩展为平衡树(如AVL树、红黑树)以优化极端情况下的性能退化。
- 20个新手学习c++必会的程序 输出*三角形、杨辉三角等(附代码)
X_StarX
c++学习算法大学生开发语言数据结构
示例1:HelloWorld#includeusingnamespacestd;intmain(){coutusingnamespacestd;intmain(){inta=5;intb=10;intsum=a+b;coutusingnamespacestd;intfactorial(intn){if(nusingnamespacestd;voidprintFibonacci(intn){intt
- C++八股
Petrichorzncu
八股总结c++开发语言
这里写目录标题C++内存管理C++的构造函数,复制构造函数,和析构函数深复制与浅复制:构造函数和析构函数哪个能写成虚函数,为什么?C++数据结构内存排列结构体和类占用的内存:==虚函数和虚表的原理==虚函数虚表(Vtable)虚函数和虚表的实现细节==内存泄漏==指针的工作原理函数的传值和传址new和delete与malloc和freeC++内存区域划分C++11新特性C++常见新特性==智能指针
- 【旅行故事】强个体与好组织相互成就@稀土永磁Amy@20220205@上海
稀土永磁Amy
我们每个人都在组织当中。当你来到组织中,都要理解个体跟组织的关系和组织中个体的关系。一个组织产生高绩效的时候,其实是需要组织个体的发展跟组织发展之间要有一个匹配程度。有时也会看到一个组织当中,一些个体会觉得发展的不够充分,原因就在于个体的发展速度超过了组织的发展速度。还有一些时候我们会发现,组织要淘汰很多个体,原因也在于组织发展的速度超越了个体发展的速度。按照这个逻辑,无论是组织的视角还是个体的视
- 【2022 CCF 非专业级别软件能力认证第一轮(CSP-J1)入门级 C++语言试题及解析】
汉子萌萌哒
CCFnoi算法数据结构c++
一、单项选择题(共15题,每题2分,共计30分;每题有且仅有一个正确选项)1.以下哪种功能没有涉及C++语言的面向对象特性支持:()。A.C++中调用printf函数B.C++中调用用户定义的类成员函数C.C++中构造一个class或structD.C++中构造来源于同一基类的多个派生类题目解析【解析】正确答案:AC++基础知识,面向对象和类有关,类又涉及父类、子类、继承、派生等关系,printf
- 《 C++ 修炼全景指南:十 》自平衡的艺术:深入了解 AVL 树的核心原理与实现
Lenyiin
C++修炼全景指南技术指南c++数据结构stl
摘要本文深入探讨了AVL树(自平衡二叉搜索树)的概念、特点以及实现细节。我们首先介绍了AVL树的基本原理,并详细分析了其四种旋转操作,包括左旋、右旋、左右双旋和右左双旋,阐述了它们在保持树平衡中的重要作用。接着,本文从头到尾详细描述了AVL树的插入、删除和查找操作,配合完整的代码实现和详尽的注释,使读者能够全面理解这些操作的执行过程。此外,我们还提供了AVL树的遍历方法,包括中序、前序和后序遍历,
- JAVA学习笔记之23种设计模式学习
victorfreedom
Java技术设计模式androidjava常用设计模式
博主最近买了《设计模式》这本书来学习,无奈这本书是以C++语言为基础进行说明,整个学习流程下来效率不是很高,虽然有的设计模式通俗易懂,但感觉还是没有充分的掌握了所有的设计模式。于是博主百度了一番,发现有大神写过了这方面的问题,于是博主迅速拿来学习。一、设计模式的分类总体来说设计模式分为三大类:创建型模式,共五种:工厂方法模式、抽象工厂模式、单例模式、建造者模式、原型模式。结构型模式,共七种:适配器
- 2022-07-06学会放手
杨晓玲乐平市第十一小学
2022年7月5日星期一晴今天结束了国培培训,上午收拾好物品,带着孩子整理心情,带着憧憬去到孩子新的学校,因为从小我有意培养孩子自己整理自己内务,孩子很认真的把自己要用的都整理好,不用的都另外装好,这一点孩子的能力还是挺强的。把自己的行李按学校提出的要求认真的整理好,我们便出发了。我们早早的来到学校,时间还早,便让她到阿姨那休息了一会儿,每去到一个新的地方,能迅速的安顿下来,这是非常好的。时间很快
- c++ opencv4.3 sift匹配
图像处理大大大大大牛啊
图像处理opencv实战代码讲解opencvsiftc++opencv4特征点
c++opencv4.3sift匹配main.cppintmain(){vectorkeypoints1,keypoints2;Matimg1,img2,descriptors1,descriptors2;intnumF
- 《 C++ 修炼全景指南:四 》揭秘 C++ List 容器背后的实现原理,带你构建自己的双向链表
Lenyiin
技术指南C++修炼全景指南c++list链表stl
本篇博客,我们将详细讲解如何从头实现一个功能齐全且强大的C++List容器,并深入到各个细节。这篇博客将包括每一步的代码实现、解释以及扩展功能的探讨,目标是让初学者也能轻松理解。一、简介1.1、背景介绍在C++中,std::list是一个基于双向链表的容器,允许高效的插入和删除操作,适用于频繁插入和删除操作的场景。与动态数组不同,list允许常数时间内的插入和删除操作,支持双向遍历。这篇文章将详细
- 这样旅行的人,值得拥有丰富而饱满的体验
究竟
01“一张车票就实现了来拉萨的梦想。原以为很遥远,现也觉得旅途值得。也不过山河故人而已。”打开朋友圈,看到了强子新发的动态,配了两张图,一张图里是拉萨火车站,另一张图里是二十来张排列得整整齐齐的火车票,终点站都是拉萨。又想起几天前,姑娘秀了一波在青海湖的美照,照片里的她,身穿鲜艳的红色长裙,坐在牦牛背上,阳光打下来,她笑靥如花。橙色的旗子风中飘扬,那蓝绿色的青海湖和天空再美,也都成了陪衬。再看看自
- c++ 内存处理函数
heeheeai
c++开发语言
在C语言的头文件中,memcpy和memmove函数都用于复制内存块,但它们在处理内存重叠方面存在关键区别:内存重叠:memcpy函数不保证在源内存和目标内存区域重叠时能够正确复制数据。如果内存区域重叠,memcpy的行为是未定义的,可能会导致数据损坏或程序崩溃。memmove函数能够安全地处理源内存和目标内存区域重叠的情况。它会确保在复制过程中不会覆盖尚未复制的数据,从而保证数据的完整性。效率:
- 【c++基础概念深度理解——堆和栈的区别,并实现堆溢出和栈溢出】
XWWW668899
C++基本概念c++c语言开发语言青少年编程
文章目录概要技术名词解释栈溢出和堆溢出小结概要学习C++语言,避免不了要好好理解一下堆(Heap)和栈(Stack),有助于更好地管理内存,以及如何写出一段程序“成功实现”堆溢出和栈溢出。技术名词解释理解东西最快的方式是根据自己目前能理解的词语去关联新的概念,不断的纠正,向正确的深度理解靠近,当无限接近的时候也就理解了想要理解的概念。我们经常说堆栈,把这两个名词放到一起。其实,堆是堆,栈是栈,两种
- 日常想打苏大强
那个是小呆呀
在没有看都挺好之前,我朋友一直都在给我安利这部剧,没看不知道,这一看不得了,这一看,每一集我都想冲进手机里,揍苏大强!我之前觉得老二很废材,啃老,对家里人不尊重,后来看了十多集之后,我觉得老二一家其实挺不错的。就拿啃老来说,确实老二一家不对,买房娶媳妇全靠家里人卖房。但是放到当今社会,大多数年轻人都是这样的,钱不够回家找爸妈,工资不够用回家找爸妈。老二还是回家找爸妈给钱的,我们有时候更省事,直接一
- 内存保护学习(一):tc27x的内存保护MPU设置浅析(个人理解)
剑从东方起
链接文件及功能安全开发语言c语言
目录一、背景二、Tc27x相关寄存器1、注意点2、注意几个强相关寄存器1)、数据保护范围寄存器2)、代码保护范围寄存器3)、保护集启用寄存器命名约定4)、PSW(每个核都有一个)5)、SYSCON三、使用方法1、内存方面2、在ECUM里面初始化MPU3、OS回调CBK检查4、机理5、补充点一、背景根据低ASIL等级开发的软件组件可能会错误地访问具有较高ASIL等级的软件组件的内存区域,从而产生干扰
- C++常见知识掌握
nfgo
c++开发语言
1.Linux软件开发、调试与维护内核与系统结构Linux内核是操作系统的核心,负责管理硬件资源,提供系统服务,它是系统软件与硬件之间的桥梁。主要组成部分包括:进程管理:内核通过调度器分配CPU时间给各个进程,实现进程的创建、调度、终止等操作。使用进程描述符(task_struct)来存储进程信息,包括状态(就绪、运行、阻塞等)、优先级、内存映射等。内存管理:包括物理内存和虚拟内存管理。通过页表映
- 算法 单链的创建与删除
换个号韩国红果果
c算法
先创建结构体
struct student {
int data;
//int tag;//标记这是第几个
struct student *next;
};
// addone 用于将一个数插入已从小到大排好序的链中
struct student *addone(struct student *h,int x){
if(h==NULL) //??????
- 《大型网站系统与Java中间件实践》第2章读后感
白糖_
java中间件
断断续续花了两天时间试读了《大型网站系统与Java中间件实践》的第2章,这章总述了从一个小型单机构建的网站发展到大型网站的演化过程---整个过程会遇到很多困难,但每一个屏障都会有解决方案,最终就是依靠这些个解决方案汇聚到一起组成了一个健壮稳定高效的大型系统。
看完整章内容,
- zeus持久层spring事务单元测试
deng520159
javaDAOspringjdbc
今天把zeus事务单元测试放出来,让大家指出他的毛病,
1.ZeusTransactionTest.java 单元测试
package com.dengliang.zeus.webdemo.test;
import java.util.ArrayList;
import java.util.List;
import org.junit.Test;
import
- Rss 订阅 开发
周凡杨
htmlxml订阅rss规范
RSS是 Really Simple Syndication的缩写(对rss2.0而言,是这三个词的缩写,对rss1.0而言则是RDF Site Summary的缩写,1.0与2.0走的是两个体系)。
RSS
- 分页查询实现
g21121
分页查询
在查询列表时我们常常会用到分页,分页的好处就是减少数据交换,每次查询一定数量减少数据库压力等等。
按实现形式分前台分页和服务器分页:
前台分页就是一次查询出所有记录,在页面中用js进行虚拟分页,这种形式在数据量较小时优势比较明显,一次加载就不必再访问服务器了,但当数据量较大时会对页面造成压力,传输速度也会大幅下降。
服务器分页就是每次请求相同数量记录,按一定规则排序,每次取一定序号直接的数据
- spring jms异步消息处理
510888780
jms
spring JMS对于异步消息处理基本上只需配置下就能进行高效的处理。其核心就是消息侦听器容器,常用的类就是DefaultMessageListenerContainer。该容器可配置侦听器的并发数量,以及配合MessageListenerAdapter使用消息驱动POJO进行消息处理。且消息驱动POJO是放入TaskExecutor中进行处理,进一步提高性能,减少侦听器的阻塞。具体配置如下:
- highCharts柱状图
布衣凌宇
hightCharts柱图
第一步:导入 exporting.js,grid.js,highcharts.js;第二步:写controller
@Controller@RequestMapping(value="${adminPath}/statistick")public class StatistickController { private UserServi
- 我的spring学习笔记2-IoC(反向控制 依赖注入)
aijuans
springmvcSpring 教程spring3 教程Spring 入门
IoC(反向控制 依赖注入)这是Spring提出来了,这也是Spring一大特色。这里我不用多说,我们看Spring教程就可以了解。当然我们不用Spring也可以用IoC,下面我将介绍不用Spring的IoC。
IoC不是框架,她是java的技术,如今大多数轻量级的容器都会用到IoC技术。这里我就用一个例子来说明:
如:程序中有 Mysql.calss 、Oracle.class 、SqlSe
- TLS java简单实现
antlove
javasslkeystoretlssecure
1. SSLServer.java
package ssl;
import java.io.FileInputStream;
import java.io.InputStream;
import java.net.ServerSocket;
import java.net.Socket;
import java.security.KeyStore;
import
- Zip解压压缩文件
百合不是茶
Zip格式解压Zip流的使用文件解压
ZIP文件的解压缩实质上就是从输入流中读取数据。Java.util.zip包提供了类ZipInputStream来读取ZIP文件,下面的代码段创建了一个输入流来读取ZIP格式的文件;
ZipInputStream in = new ZipInputStream(new FileInputStream(zipFileName));
&n
- underscore.js 学习(一)
bijian1013
JavaScriptunderscore
工作中需要用到underscore.js,发现这是一个包括了很多基本功能函数的js库,里面有很多实用的函数。而且它没有扩展 javascript的原生对象。主要涉及对Collection、Object、Array、Function的操作。 学
- java jvm常用命令工具——jstatd命令(Java Statistics Monitoring Daemon)
bijian1013
javajvmjstatd
1.介绍
jstatd是一个基于RMI(Remove Method Invocation)的服务程序,它用于监控基于HotSpot的JVM中资源的创建及销毁,并且提供了一个远程接口允许远程的监控工具连接到本地的JVM执行命令。
jstatd是基于RMI的,所以在运行jstatd的服务
- 【Spring框架三】Spring常用注解之Transactional
bit1129
transactional
Spring可以通过注解@Transactional来为业务逻辑层的方法(调用DAO完成持久化动作)添加事务能力,如下是@Transactional注解的定义:
/*
* Copyright 2002-2010 the original author or authors.
*
* Licensed under the Apache License, Version
- 我(程序员)的前进方向
bitray
程序员
作为一个普通的程序员,我一直游走在java语言中,java也确实让我有了很多的体会.不过随着学习的深入,java语言的新技术产生的越来越多,从最初期的javase,我逐渐开始转变到ssh,ssi,这种主流的码农,.过了几天为了解决新问题,webservice的大旗也被我祭出来了,又过了些日子jms架构的activemq也开始必须学习了.再后来开始了一系列技术学习,osgi,restful.....
- nginx lua开发经验总结
ronin47
使用nginx lua已经两三个月了,项目接开发完毕了,这几天准备上线并且跟高德地图对接。回顾下来lua在项目中占得必中还是比较大的,跟PHP的占比差不多持平了,因此在开发中遇到一些问题备忘一下 1:content_by_lua中代码容量有限制,一般不要写太多代码,正常编写代码一般在100行左右(具体容量没有细心测哈哈,在4kb左右),如果超出了则重启nginx的时候会报 too long pa
- java-66-用递归颠倒一个栈。例如输入栈{1,2,3,4,5},1在栈顶。颠倒之后的栈为{5,4,3,2,1},5处在栈顶
bylijinnan
java
import java.util.Stack;
public class ReverseStackRecursive {
/**
* Q 66.颠倒栈。
* 题目:用递归颠倒一个栈。例如输入栈{1,2,3,4,5},1在栈顶。
* 颠倒之后的栈为{5,4,3,2,1},5处在栈顶。
*1. Pop the top element
*2. Revers
- 正确理解Linux内存占用过高的问题
cfyme
linux
Linux开机后,使用top命令查看,4G物理内存发现已使用的多大3.2G,占用率高达80%以上:
Mem: 3889836k total, 3341868k used, 547968k free, 286044k buffers
Swap: 6127608k total,&nb
- [JWFD开源工作流]当前流程引擎设计的一个急需解决的问题
comsci
工作流
当我们的流程引擎进入IRC阶段的时候,当循环反馈模型出现之后,每次循环都会导致一大堆节点内存数据残留在系统内存中,循环的次数越多,这些残留数据将导致系统内存溢出,并使得引擎崩溃。。。。。。
而解决办法就是利用汇编语言或者其它系统编程语言,在引擎运行时,把这些残留数据清除掉。
- 自定义类的equals函数
dai_lm
equals
仅作笔记使用
public class VectorQueue {
private final Vector<VectorItem> queue;
private class VectorItem {
private final Object item;
private final int quantity;
public VectorI
- Linux下安装R语言
datageek
R语言 linux
命令如下:sudo gedit /etc/apt/sources.list1、deb http://mirrors.ustc.edu.cn/CRAN/bin/linux/ubuntu/ precise/ 2、deb http://dk.archive.ubuntu.com/ubuntu hardy universesudo apt-key adv --keyserver ke
- 如何修改mysql 并发数(连接数)最大值
dcj3sjt126com
mysql
MySQL的连接数最大值跟MySQL没关系,主要看系统和业务逻辑了
方法一:进入MYSQL安装目录 打开MYSQL配置文件 my.ini 或 my.cnf查找 max_connections=100 修改为 max_connections=1000 服务里重起MYSQL即可
方法二:MySQL的最大连接数默认是100客户端登录:mysql -uusername -ppass
- 单一功能原则
dcj3sjt126com
面向对象的程序设计软件设计编程原则
单一功能原则[
编辑]
SOLID 原则
单一功能原则
开闭原则
Liskov代换原则
接口隔离原则
依赖反转原则
查
论
编
在面向对象编程领域中,单一功能原则(Single responsibility principle)规定每个类都应该有
- POJO、VO和JavaBean区别和联系
fanmingxing
VOPOJOjavabean
POJO和JavaBean是我们常见的两个关键字,一般容易混淆,POJO全称是Plain Ordinary Java Object / Plain Old Java Object,中文可以翻译成:普通Java类,具有一部分getter/setter方法的那种类就可以称作POJO,但是JavaBean则比POJO复杂很多,JavaBean是一种组件技术,就好像你做了一个扳子,而这个扳子会在很多地方被
- SpringSecurity3.X--LDAP:AD配置
hanqunfeng
SpringSecurity
前面介绍过基于本地数据库验证的方式,参考http://hanqunfeng.iteye.com/blog/1155226,这里说一下如何修改为使用AD进行身份验证【只对用户名和密码进行验证,权限依旧存储在本地数据库中】。
将配置文件中的如下部分删除:
<!-- 认证管理器,使用自定义的UserDetailsService,并对密码采用md5加密-->
- mac mysql 修改密码
IXHONG
mysql
$ sudo /usr/local/mysql/bin/mysqld_safe –user=root & //启动MySQL(也可以通过偏好设置面板来启动)$ sudo /usr/local/mysql/bin/mysqladmin -uroot password yourpassword //设置MySQL密码(注意,这是第一次MySQL密码为空的时候的设置命令,如果是修改密码,还需在-
- 设计模式--抽象工厂模式
kerryg
设计模式
抽象工厂模式:
工厂模式有一个问题就是,类的创建依赖于工厂类,也就是说,如果想要拓展程序,必须对工厂类进行修改,这违背了闭包原则。我们采用抽象工厂模式,创建多个工厂类,这样一旦需要增加新的功能,直接增加新的工厂类就可以了,不需要修改之前的代码。
总结:这个模式的好处就是,如果想增加一个功能,就需要做一个实现类,
- 评"高中女生军训期跳楼”
nannan408
首先,先抛出我的观点,各位看官少点砖头。那就是,中国的差异化教育必须做起来。
孔圣人有云:有教无类。不同类型的人,都应该有对应的教育方法。目前中国的一体化教育,不知道已经扼杀了多少创造性人才。我们出不了爱迪生,出不了爱因斯坦,很大原因,是我们的培养思路错了,我们是第一要“顺从”。如果不顺从,我们的学校,就会用各种方法,罚站,罚写作业,各种罚。军
- scala如何读取和写入文件内容?
qindongliang1922
javajvmscala
直接看如下代码:
package file
import java.io.RandomAccessFile
import java.nio.charset.Charset
import scala.io.Source
import scala.reflect.io.{File, Path}
/**
* Created by qindongliang on 2015/
- C语言算法之百元买百鸡
qiufeihu
c算法
中国古代数学家张丘建在他的《算经》中提出了一个著名的“百钱买百鸡问题”,鸡翁一,值钱五,鸡母一,值钱三,鸡雏三,值钱一,百钱买百鸡,问翁,母,雏各几何?
代码如下:
#include <stdio.h>
int main()
{
int cock,hen,chick; /*定义变量为基本整型*/
for(coc
- Hadoop集群安全性:Hadoop中Namenode单点故障的解决方案及详细介绍AvatarNode
wyz2009107220
NameNode
正如大家所知,NameNode在Hadoop系统中存在单点故障问题,这个对于标榜高可用性的Hadoop来说一直是个软肋。本文讨论一下为了解决这个问题而存在的几个solution。
1. Secondary NameNode
原理:Secondary NN会定期的从NN中读取editlog,与自己存储的Image进行合并形成新的metadata image
优点:Hadoop较早的版本都自带,