分布式事务之底层原理揭秘

  

，

  hi 大家好，今天分享一这篇文章，让大家彻底了解分布式原理，这个是后台开发必须掌握技能。

• 刚性事务

• 柔性事务

• 本地事务

• 分布式事务

• 单阶段原子提交协议

• 两阶段提交协议

• • 定义

  • 原理

  • 性能

  • 恢复

  • 缺陷

  • XA 标准接口

  • 三阶段提交协议

• Paxos

• • Basic Paxos

  • Multi-Paxos

• Raft

• 算法类型

• 锁并发控制

• 时间戳并发控制

• 乐观并发控制

导言

分布式事务是分布式系统必不可少的组成部分，基本上只要实现一个分布式系统就逃不开对分布式事务的支持。本文从分布式事务这个概念切入，尝试对分布式事务以及分布式系统最核心的底层原理逐一进行剖析，内容包括但不限于 BASE 原则、两阶段原子提交协议、三阶段原子提交协议、Paxos/Multi-Paxos 分布式共识算法的原理与证明、Raft 分布式共识算法和分布式事务的并发控制等内容。

事务

事务是访问并可能更新各种数据项的一个程序执行单元(unit)。事务由一个或多个步骤组成，一般使用形如 begin transaction 和 end transaction 语句或者函数调用作为事务界限，事务内的所有步骤必须作为一个单一的、不可分割的单元去执行，因此事务的结果只有两种：1. 全部步骤都执行完成，2. 任一步骤执行失败则整个事务回滚。

事务最早由数据库管理系统(database management system，DBMS)引入并实现，数据库事务是数据库管理系统执行过程中的一个逻辑单位，由一个有限的数据库操作序列构成。数据库事务严格遵循 ACID 原则，属于刚性事务，一开始数据库事务仅限于对单一数据库资源对象的访问控制，这一类事务称之为本地事务 (Local Transaction)，后来随着分布式系统的出现，数据的存储也不可避免地走向了分布式，分布式事务（Distributed Transaction）便应运而生。

刚性事务

刚性事务（如单一数据库事务）完全遵循 ACID 规范，即数据库事务的四大基本特性：

• Atomicity（原子性）：一个事务（transaction）中的所有操作，或者全部完成，或者全部不完成，不会结束在中间某个环节。事务在执行过程中发生错误，会被回滚（Rollback）到事务开始前的状态，就像这个事务从来没有执行过一样。即，事务不可分割、不可约简。

• Consistency（一致性）：在事务开始之前和事务结束以后，数据库的完整性没有被破坏。这表示写入的资料必须完全符合所有的预设约束、触发器、级联回滚等。

• Isolation（隔离性）：数据库允许多个并发事务同时对其数据进行读写和修改的能力，隔离性可以防止多个事务并发执行时由于交叉执行而导致数据的不一致。事务隔离分为不同级别，包括未提交读（Read uncommitted）、提交读（read committed）、可重复读（repeatable read）和串行化（Serializable）。

• Durability（持久性）：事务处理结束后，对数据的修改就是永久的，即便系统故障也不会丢失。

刚性事务也能够以分布式 CAP 理论中的 CP 事务来作为定义。

柔性事务

在电商领域等互联网场景下，传统的事务在数据库性能和处理能力上都遇到了瓶颈。因此，柔性事务被提了出来，柔性事务基于分布式 CAP 理论以及延伸出来的 BASE 理论，相较于数据库事务这一类完全遵循 ACID 的刚性事务来说，柔性事务保证的是 “基本可用，最终一致”，CAP 原理相信大家都很熟悉了，这里我们讲一下 BASE 原则：

• 基本可用（Basically Available）：系统能够基本运行、一直提供服务。

• 软状态（Soft-state）：系统不要求一直保持强一致状态。

• 最终一致性（Eventual consistency）：系统需要在某一时刻后达到一致性要求。

柔性事务（如分布式事务）为了满足可用性、性能与降级服务的需要，降低一致性（Consistency）与隔离性（Isolation）的要求，遵循 BASE 理论，传统的 ACID 事务对隔离性的要求非常高，在事务执行过程中，必须将所有的资源对象锁定，因此对并发事务的执行极度不友好，柔性事务（比如分布式事务）的理念则是将锁资源对象操作从本地资源对象层面上移至业务逻辑层面，再通过放宽对强一致性要求，以换取系统吞吐量的提升。

此外，虽然柔性事务遵循的是 BASE 理论，但是还需要遵循部分 ACID 规范：

• 原子性：严格遵循。

• 一致性：事务完成后的一致性严格遵循；事务中的一致性可适当放宽。

• 隔离性：并行事务间不可影响；事务中间结果可见性允许安全放宽。

• 持久性：严格遵循。

本地事务

本地事务（Local Transaction）指的是仅仅对单一节点/数据库资源对象进行访问/更新的事务，在这种事务模式下，BASE 理论派不上用场，事务完全遵循 ACID 规范，确保事务为刚性事务。

分布式事务

在分布式架构成为主流的当下，系统对资源对象的访问不能还局限于单节点，多服务器、多节点的资源对象访问成为刚需，因此，本地事务无法满足分布式架构的系统的要求，分布式事务应运而生。

访问/更新由多个服务器管理的资源对象的平面事务或者嵌套事务称之为分布式事务（Distributed Transaction），分布式事务是相对于本地事务来说的。

平面事务：单一事务，访问多个服务器节点的资源对象，一个平面事务完成一次请求之后才能发起下一个请求。

嵌套事务：多事务组成，顶层事务可以不断创建子事务，子事务又可以进一步地以任意深度嵌套子事务。

对于分布式事务来说，有两个最核心的问题：

1. 如何管理分布式事务的提交/放弃决定？如果事务中的一个节点在执行自己的本地事务过程中遇到错误，希望放弃整个分布式事务，与此同时其他节点则在事务执行过程中一切顺利，希望提交这个分布式事务，此时我们应该如何做决策？

2. 如何保证并发事务在涉及多个节点上资源对象访问的可串行性（规避分布式死锁）？如果事务 T 对某一个服务器节点上的资源对象 S 的并发访问在事务 U 之前，那么我们需要保证在所有服务器节点上对 S 和其他资源对象的冲突访问，T 始终在 U 之前。

问题 1 的解决需要引入一类分布式原子提交协议的算法如两阶段提交协议等，来对分布式事务过程中的提交或放弃决策进行管理，并确保分布式提交的原子性。而问题 2 则由分布式事务的并发控制机制来处理。

原子提交协议

原子性是分布式事务的前置性约束，没有原子性则分布式事务毫无意义。

原子性约束要求在分布式事务结束之时，它的所有操作要么全部执行，要么全部不执行。以分布式事务的原子性来分析，客户端请求访问/更新多个服务器节点上的资源对象，在客户端提交或放弃该事务从而结束事务之后，多个服务器节点的最终状态要么是该事务里的所有步骤都执行成功之后的状态，要么恢复到事务开始前的状态，不存在中间状态。满足这种约束的分布式事务协议则称之为原子提交协议。

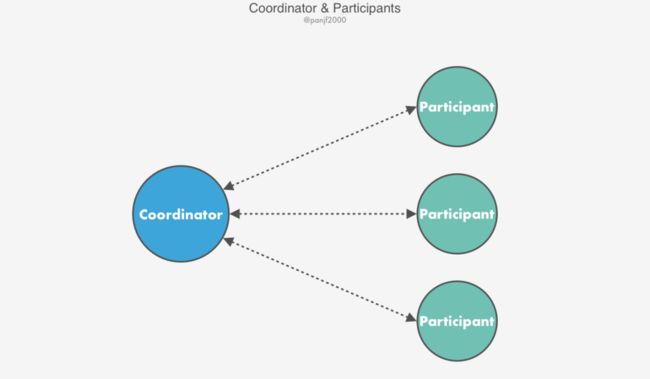
当一个分布式事务结束时，事务的原子特性要求所有参与该事务的服务器节点必须全部提交或者全部放弃该事务，为了实现这一点，必须引入一个协调者（Coordinator）的角色，从参与事务的所有服务器节点中挑选一个作为协调者，由它来保证在所有服务器节点上最终获得同样的结果。协调者的工作原理取决于分布式事务选用的协议。

一般来说，分布式事务中包含的两个最基础的角色就是：

• Coordinator -- 协调者

• Participants -- 参与者

单阶段原子提交协议

单阶段原子提交协议（one-phase atomic commit protocol, 1APC）是最简单的一种原子提交协议，它通过设置一个协调者并让它不断地向所有参与者发送提交（commit）或放弃（abort）事务的请求，直到所有参与者确认已执行完相应的操作。

1APC 协议的优点是简单易用，对一些事务不复杂的场景比较合适，但在复杂事务场景则显得捉襟见肘，因为该协议不允许任何服务器节点单方面放弃事务，事务的放弃必须由协调者来发起，这个设计会导致很多问题：首先因为只有一次通信，协调者并不会收集所有参与者的本地事务执行的情况，所以协调者决定提交还是放弃事务只基于自己的判断，在参与者执行事务期间可能会遇到错误从而导致最终事务未能真正提交，错误一般与事务的并发控制有关，比如事务执行期间对资源对象加锁，遇到死锁，需要放弃事务从而解开死锁，而协调者并不知道，因此在发起下一个请求之前，客户端完全不知道事务已被放弃。另一种情况就是利用乐观并发控制机制访问资源对象，某一个服务器节点的验证失败将导致事务被放弃，而协调者完全不知情。

两阶段提交协议

定义

两阶段提交协议（two-phase commit protocol, 2PC）的设计初衷是为了解决 1APC 不允许任意一个服务器节点自行放弃它自己的那部分本地事务的痛点，2PC 允许任何一个参与者自行决定要不要放弃它的本地事务，而由于原子提交协议的约束，任意一个本地事务被放弃将导致整个分布式事务也必须放弃掉。

两阶段提交协议基于以下几个假设：

• 存在一个节点作为协调者（Coordinator），分布式事务通常由协调者发起（当然也可以由参与者发起），其余节点作为参与者（Participants），且节点之间可以自由地进行网络通信，协调者负责启动两阶段提交流程以及决定事务最终是被提交还是放弃。

• 每个节点会记录该节点上的本地操作日志（op logs），日志必须持久化在可靠的存储设备上（比如磁盘），以便在节点重启之后需要恢复操作日志。另外，不记录全局操作日志。

• 所有节点不能发生永久性损坏，也就是说节点就算是损坏了也必须能通过可靠性存储恢复如初，不允许出现数据永久丢失的情况。

• 参与者对协调者的回复必须要去除掉那些受损和重复的消息。

• 整个集群不会出现拜占庭故障（Byzantine Fault）-- 服务器要么崩溃，要么服从其发送的消息。

原理

两阶段提交协议，顾名思义整个过程需要分为两个阶段：

1. 准备阶段（Prepare Phase）

2. 提交阶段（Commit Phase）

在进行两阶段提交的过程中，协调者会在以下四种状态间流转：

1. init

2. preparing

3. committed

4. aborted

而参与者则会在以下三种状态间流转：

1. working

2. prepared

3. committed

阶段 I（投票表决阶段）

1. 任意一个参与者发起分布式事务 T 并执行本地事务成功，接着将一条 记录追加到本地日志 buffer 中并 flush 到可靠性存储设备如磁盘上，从 working 状态进入 prepared 状态，然后向协调者发送 prepare T 消息；

2. 收到参与者发来的 prepare T 消息后，协调者将一条 记录追加到日志中，然后从 init 状态进入 preparing 状态，紧接着向分布式事务的其他参与者发出 canCommit? 消息，发起事务表决过程；

3. 当参与者收到 canCommit? 请求后，除了发起事务的那一个之外，其他还在 working 状态的参与者会先尝试执行本地事务，如果本地事务执行成功，则会往本地日志 buffer 写入一条 记录并 flush 到可靠性存储中，但不提交事务，进入 prepared 状态，然后回复一条 ready T 消息对此事务投 YES 票；如果本地事务执行失败，则参与者会往本地日志 buffer 写入一条 记录并 flush 到可靠性存储中，然后回复一条 don't commit T 消息投 NO 票。

阶段 II（收集投票结果完成事务）

1. 协调者收集所有的投票（包括它自己的投票）；

   (a) 如果所有的投票都是 ready T，则表示没有故障发生，那么协调者决定提交该事务，首先它会在其本地日志中追加一条 记录，从 preparing 状态进入 committed 状态，然后向所有的参与者发送 doCommit 请求消息，要求参与者提交它们的本地事务；

   (b) 如果有任一个投票是 No，则协调者决定放弃掉该事务，首先它会往本地日志中追加一条记录，从 preparing 状态进入 aborted 状态，然后发送 doAbort 请求消息给所有的参与者，通知它们回滚各自的本地事务。

2. 投了 YES 票的参与者阻塞等待协调者给它发来 doCommit 或 doAbort 消息，如果接收到的是 doCommit 消息则提交本地事务并在此过程中记录日志 ，然后进入 committed 状态，最后回复一个 haveCommitted 的消息通知协调者本地事务已经成功提交；反之，如果收到的是 doAbort 消息则回滚本地事务并写入日志 ，然后进入 aborted状态。

上面的过程是一种更通用的流程，即由任意的参与者发起一个分布式事务，而在实践中一般把分布式事务的发起交给协调者来做，减少事务发起者确认该事务已被提交所需等待的网络消息延迟：

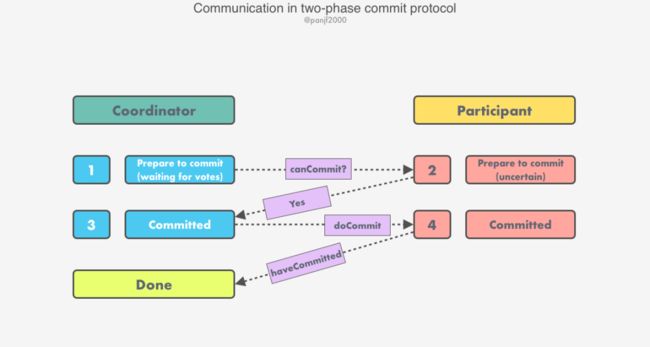
性能

网络 I/O 开销

假设两阶段提交过程一切运行正常，即协调者和参与者都不出现崩溃和重启，网络通信也都正常。那么假设有一个协调者和 N 个参与者，两阶段提交过程中将会发送如下的消息：

• 任意一个参与者从 working 状态进入 prepared 状态并发送 Prepared 消息给协调者，1 条消息。

• 协调者收到消息后，向其他参与者发送 canCommit? 请求消息，N - 1 条消息。

• 收到 canCommit? 消息的参与者各自回复协调者投票消息，N - 1 条消息。

• 协调者统计投票情况之后，发送 doCommit 消息给其他参与者，N 条消息。

所以，事务发起者在经过 4 条网络消息延迟之后确认该分布式事务已被提交，而整个过程共计发送 3N - 1 条网络消息（因为 haveCommitted 在 2PC 仅仅是用于最后通知协调者而已，属于可有可无的一次网络消息，2PC 在该消息缺省的情况下也能正常运行，因此 haveCommitted 一般不计入网络延迟成本中）。

前面我们提到，在实践中一般是由协调者来发起事务，如果考虑这种情况的话，事务发起者 -- 协调者在经过 3 条网络消息延迟之后确认该分布式事务已经被提交，而整个过程实际发送的网络消息则变成 3N 条。

总而言之，两阶段提交协议的网络通信开销和集群节点的数量成 3 倍正比。

本地存储设备 I/O 开销

基于前文中叙述的两阶段提交协议的基本假设之一：每个节点会通过日志来记录在本地执行的操作，以便在节点发生故障并重启节点之后能利用日志恢复到故障前的状态，因此两阶段提交过程中除了网络 I/O 的开销之外，还有本地存储设备 I/O 的开销：

• 发起事务的参与者执行本地事务，1 次写操作。

• 其余参与者执行各自的本地事务，N - 1 次写操作。

• 协调者统计投票结果并决定提交事务，1 次写操作。

所以事务发起者在经过 3 次本地存储设备 I/O 延迟之后确认该事务已被提交，整个过程总计有 N + 1 次本地存储设备 I/O，而如果由协调者来发起事务的话，则还是需要 N + 1 次本地存储设备 I/O，但是只需要经过 2 次本地存储设备 I/O 延迟即可确认事务已被提交。

恢复

在分布式事务中，所有的参与者节点都可能发生故障，所以我们需要保证在该故障节点恢复时发生的一切都和分布式事务 T 的全局决策保持一致。节点在恢复的时候会读取 T 的最后一个本地日志记录并作出相应的操作：

1. 如果 T 的最后一条日志记录是 ，那么说明协调者在节点发生故障时的全局决策是提交 T，根据本地事务所使用的日志方式，在该节点上可能需要执行 redo T。

2. 如果 T 的最后一条日志记录是 ，那么说明协调者在节点发生故障时的全局决策是中止 T，根据本地事务所使用的日志方式，在该节点上可能需要执行 undo T。

3. 如果 T 的最后一条日志记录是 ，则和第 2 中情况类似，执行 undo T。

4. 如果 T 的最后一条日志记录是 ，这种情况比较麻烦，因为恢复节点无法确认在它故障之后协调者发出的最终全局决策是什么，因此它必须要和集群中其余至少一个节点取得联系，询问 T 的最终结果是什么：恢复节点先尝试询问协调者，如果此时协调者正在工作，则告知恢复节点 T 的最终结果，如果是提交就执行 redo T，中止就执行 undo T；如果协调者因故不在工作，则恢复节点可以要求其他某一个参与者节点去查看本地日志以找出 T 的最终结果并告知恢复节点。在最坏的情况下，恢复节点无法和集群中其他所有节点取得联系，这时恢复节点只能阻塞等待，直至得知 T 的最终结果是提交还是中止。

5. 如果本地日志中没有记录任何关于 T 在两阶段提交过程中的操作，那么根据前面的两阶段提交流程可知恢复节点还没来得及回复协调者的 canCommit? 请求消息就发生了故障，因此根据两阶段算法，恢复节点只能执行 undo T。

缺陷

1. 同步阻塞：两阶段提交协议是一个阻塞的协议，在第二阶段期间，参与者在事务未提交之前会一直锁定其占有的本地资源对象，直到接收到来自协调者的 doCommit 或 doAbort 消息。

2. 单点故障：两阶段提交协议中只有一个协调者，而由于在第二阶段中参与者在收到协调者的进一步指示之前会一直锁住本地资源对象，如果唯一的协调者此时出现故障而崩溃掉之后，那么所有参与者都将无限期地阻塞下去，也就是一直锁住本地资源对象而导致其他进程无法使用。

3. 数据不一致：如果在两阶段提交协议的第二阶段中，协调者向所有参与者发送 doCommit 消息之后，发生了局部网络抖动或者异常，抑或是协调者在只发送了部分消息之后就崩溃了，那么就只会有部分参与者接收到了 doCommit 消息并提交了本地事务；其他未收到 doCommit 消息的参与者则不会提交本地事务，因而导致了数据不一致问题。

XA 标准接口

2PC 两阶段提交协议本身只是一个通用协议，不提供具体的工程实现的规范和标准，在工程实践中为了统一标准，减少行业内不必要的对接成本，需要制定标准化的处理模型及接口标准，国际开放标准组织 Open Group 定义了分布式事务处理模型 DTP（Distributed Transaction Processing）Model，现在 XA 已经成为 2PC 分布式事务提交的事实标准，很多主流数据库如 Oracle、MySQL 等都已经实现 XA。

两阶段事务提交采用的是 X/OPEN 组织所定义的 DTP Model 所抽象的 AP（应用程序）, TM（事务管理器）和 RM（资源管理器） 概念来保证分布式事务的强一致性。其中 TM 与 RM 间采用 XA 的协议进行双向通信。与传统的本地事务相比，XA 事务增加了准备阶段，数据库除了被动接受提交指令外，还可以反向通知调用方事务是否可以被提交。TM 可以收集所有分支事务的准备结果，并于最后进行原子提交，以保证事务的强一致性。

Java 通过定义 JTA 接口实现了 XA 模型，JTA 接口中的 ResourceManager 需要数据库厂商提供 XA 驱动实现， TransactionManager 则需要事务管理器的厂商实现，传统的事务管理器需要同应用服务器绑定，因此使用的成本很高。而嵌入式的事务管器可以以 jar 包的形式提供服务，同 Apache ShardingSphere 集成后，可保证分片后跨库事务强一致性。

通常，只有使用了事务管理器厂商所提供的 XA 事务连接池，才能支持 XA 的事务。Apache ShardingSphere 在整合 XA 事务时，采用分离 XA 事务管理和连接池管理的方式，做到对应用程序的零侵入。

三阶段提交协议

由于前文提到的两阶段提交协议的种种弊端，研究者们后来又提出了一种新的分布式原子提交协议：三阶段提交协议（three-phase commit protocol, 3PC）。

三阶段提交协议是对两阶段提交协议的扩展，它在特定假设下避免了同步阻塞的问题。该协议基于以下两个假设：

1. 集群不发生网络分区；

2. 故障节点数不超过 K 个（K 是预先设定的一个数值）。

基于这两个假设，三阶段提交协议通过引入超时机制和一个额外的阶段来解决阻塞问题，三阶段提交协议把两阶段提交协议的第一个阶段拆分成了两步：1) 评估，2) 资源对象加锁，最后才真正提交：

1. CanCommit 阶段：协调者发送 CanCommit 请求消息，询问各个参与者节点，参与者节点各自评估本地事务是否可以执行并回复消息（可以执行则回复 YES，否则回复 NO），此阶段不执行事务，只做判断；

2. PreCommit 阶段：协调者根据上一阶段收集的反馈决定通知各个参与者节点执行（但不提交）或中止本地事务；有两种可能：1) 所有回复都是 YES，则发送 PreCommit 请求消息，要求所有参与者执行事务并追加记录到 undo 和 redo 日志，如果事务执行成功则参与者回复 ACK 响应消息，并等待下一阶段的指令；2) 反馈消息中只要有一个 NO，或者等待超时之后协调者都没有收到参与者的回复，那么协调者会中止事务，发送 Abort 请求消息给所有参与者，参与者收到该请求后中止本地事务，或者参与者超时等待仍未收到协调者的消息，同样也中止当前本地事务。

3. DoCommit 阶段：协调者根据上一阶段收集到的反馈决定通知各个参与者节点提交或回滚本地事务，分三种情况：1) 协调者收到全部参与者回复的 ACK，则向所有参与者节点广播 DoCommit 请求消息，各个参与者节点收到协调者的消息之后决定提交事务，然后释放资源对象上的锁，成功之后向协调者回复 ACK，协调者接收到所有参与者的 ACK 之后，将该分布式事务标记为 committed；2) 协调者没有收到全部参与者回复的 ACK（可能参与者回复的不是 ACK，也可能是消息丢失导致超时），那么协调者就会中止事务，首先向所有参与者节点广播 Abort 请求消息，各个参与者收到该消息后利用上一阶段的 undo 日志进行事务的回滚，释放占用的资源对象，然后回复协调者 ACK 消息，协调者收到参与者的 ACK 消息后将该分布式事务标记为 aborted；3) 参与者一直没有收到协调者的消息，等待超时之后会直接提交事务。

事实上，在最后阶段，协调者不是通过追加本地日志的方式记录提交决定的，而是首先保证让至少 K 个参与者节点知道它决定提交该分布式事务。如果协调者发生故障了，那么剩下的参与者节点会重新选举一个新的协调者，这个新的协调者就可以在集群中不超过 K 个参与者节点故障的情况下学习到旧协调者之前是否已经决定要提交分布式事务，若是，则重新开始协议的第三阶段，否则就中止该事务，重新发起分布式事务。

在最后的 DoCommit 阶段，如果参与者一直没有收到协调者的 DoCommit 或者 Abort 请求消息时，会在等待超时之后，直接提交事务。这个决策机制是基于概率学的：当已经进入第三阶段之后，说明参与者在第二阶段已经收到了 PreCommit 请求消息，而协调者发出 PreCommit 请求的前提条件是它在第二阶段开头收集到的第一阶段向所有参与者发出的 CanCommit 请求消息的反馈消息都是 YES。所以参与者可以根据自己收到了 PreCommit 请求消息这一既定事实得出这样的一个结论：其他所有参与者都同意了进行这次的事务执行，因此当前的参与者节点有理由相信，进入第三阶段后，其他参与者节点的本地事务最后成功提交的概率很大，而自己迟迟没有收到 DoCommit 或 Abort 消息可能仅仅是因为网络抖动或异常，因此直接提交自己的本地事务是一个比较合理的选择。

三阶段提交协议主要着重于解决两阶段提交协议中因为协调者单点故障而引发的同步阻塞问题，虽然相较于两阶段提交协议有所优化，但还是没解决可能发生的数据不一致问题，比如由于网络异常导致部分参与者节点没有收到协调者的 Abort 请求消息，超时之后这部分参与者会直接提交事务，从而导致集群中的数据不一致，另外三阶段提交协议也无法解决脑裂问题，同时也因为这个协议的网络开销问题，导致它并没有被广泛地使用，有关该协议的具体细节可以参阅本文最后的延伸阅读一节中的文献进一步了解，这里不再深入。

共识算法

共识（Consensus），很多时候会见到与一致性（Consistency）术语放在一起讨论。严谨地讲，两者的含义并不完全相同。

一致性的含义比共识宽泛，在不同场景（基于事务的数据库、分布式系统等）下意义不同。具体到分布式系统场景下，一致性指的是多个副本对外呈现的状态。如前面提到的顺序一致性、线性一致性，描述了多节点对数据状态的共同维护能力。而共识，则特指在分布式系统中多个节点之间对某个事情（例如多个事务请求，先执行谁？）达成一致意见的过程。因此，达成某种共识并不意味着就保障了一致性。

实践中，要保证系统满足不同程度的一致性，往往需要通过共识算法来达成。

共识算法解决的是分布式系统对某个提案（Proposal），大部分节点达成一致意见的过程。提案的含义在分布式系统中十分宽泛，如多个事件发生的顺序、某个键对应的值、谁是主节点……等等。可以认为任何可以达成一致的信息都是一个提案。

对于分布式系统来讲，各个节点通常都是相同的确定性状态机模型（又称为状态机复制问题，State-Machine Replication），从相同初始状态开始接收相同顺序的指令，则可以保证相同的结果状态。因此，系统中多个节点最关键的是对多个事件的顺序进行共识，即排序。

算法共识/一致性算法有两个最核心的约束：1) 安全性（Safety），2) 存活性（Liveness）：

• Safety：保证决议（Value）结果是对的，无歧义的，不会出现错误情况。

• • 只有是被提案者提出的提案才可能被最终批准；

  • 在一次执行中，只批准（chosen）一个最终决议。被多数接受（accept）的结果成为决议；

• Liveness：保证决议过程能在有限时间内完成。

• • 决议总会产生，并且学习者最终能获得被批准的决议。

Paxos

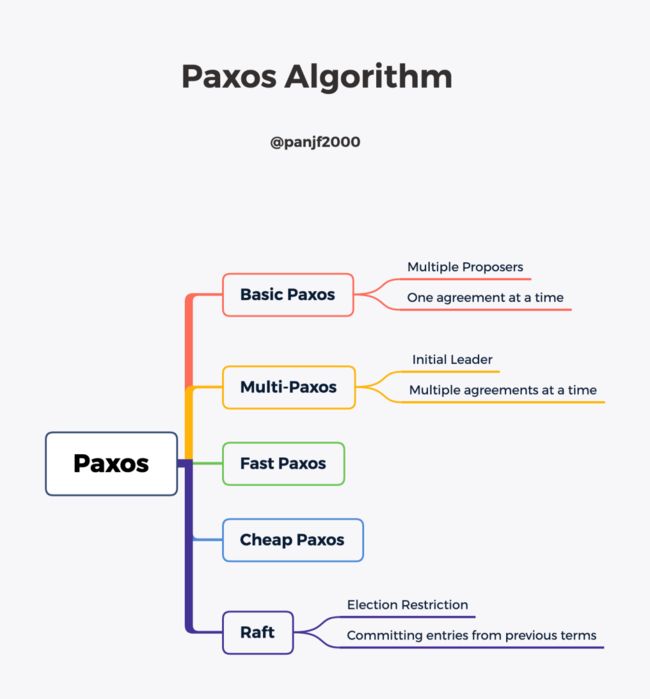
Google Chubby 的作者 Mike Burrows 说过， there is only one consensus protocol, and that’s Paxos” – all other approaches are just broken versions of Paxos.

意即世上只有一种共识算法，那就是 Paxos，其他所有的共识算法都只是 Paxos 算法的残缺版本。虽然有点武断，但是自从 Paxos 问世以来，它便几乎成为了分布式共识算法的代名词，后来的许多应用广泛的分布式共识算法如 Raft、Zab 等的原理和思想都可以溯源至 Paxos 算法。

Paxos 是由 Leslie Lamport (LaTeX 发明者，图灵奖得主，分布式领域的世界级大师) 在 1990 年的论文《The PartTime Parliament》里提出的，Lamport 在论文中以一个古希腊的 Paxos 小岛上的议会制订法律的故事切入，引出了 Paxos 分布式共识算法。

Basic Paxos

业界一般将 Lamport 论文里最初提出分布式算法称之为 Basic Paxos，这是 Paxos 最基础的算法思想。

Basic Paxos 算法的最终目标是通过严谨和可靠的流程来使得集群基于某个提案（Proposal）达到最终的共识。

基础概念

• Value：提案值，是一个抽象的概念，在工程实践中可以是任何操作，如『更新数据库某一行的某一列』、『选择 xxx 服务器节点作为集群中的主节点』。

• Number：提案编号，全局唯一，单调递增。

• Proposal：集群需要达成共识的提案，提案 = 编号 + 值。

Proposal 中的 Value 就是在 Paxos 算法完成之后需要达成共识的值。

Paxos 算法中有三个核心角色：

• Proposer：生成提案编号 n 和值 v，然后向 Acceptors 广播该提案，接收 Acceptors 的回复，如果有超过半数的 Acceptors 同意该提案，则选定该提案，否则放弃此次提案并生成更新的提案重新发起流程，提案被选定之后则通知所有 Learners 学习该最终选定的提案值（也可以由 Acceptor 来通知，看具体实现）。Basic Paxos 中允许有多个 Proposers。

• Acceptor：接收 Proposer 的提案并参与提案决策过程，把各自的决定回复给 Proposer 进行统计。Acceptor 可以接受来自多个 proposers 的多个提案。

• Learner：不参与决策过程，只学习最终选定的提案值。

在具体的工程实践中，一个节点往往会充当多种角色，比如一个节点可以既是 Proposer 又是 Acceptor，甚至还是 Learner。

算法流程

相较于直接给出 Paxos 算法的流程，我想沿袭 Lamport 大师的经典 Paxos 论文《Paxos Made Simple》中的思路：通过循序渐进的方式推导出 Paxos 算法。

首先需要了解 Paxos 算法中的两个重要的约束：

C1. 一个 Acceptor 必须接受它收到的第一个提案。

C2. 只有当超过半数的 Acceptors 接受某一个提案，才能最终选定该提案。

C2 其实有一个隐含的推论：一个 Acceptor 可以接受多个提案，这也是为什么我们需要给每一个提案生成一个编号的原因，用来给提案排序。

我们前面提到过 Paxos 的最终目标是通过严谨和可靠的流程来使得集群基于某个提案（Proposal）达到最终的共识，也就是说基于某一个提案发起的一次 Paxos 流程，最终目的是希望集群对该提案达成一致的意见，而为了实现并维持集群中的这种一致性，前提是 Paxos 算法必须具有幂等性：一旦提案（Proposal）中的值（Value）被选定（Chosen），那么只要还在此次 Paxos 流程中，就算不断按照 Paxos 的规则重复步骤，未来被 Chosen 的 Value 都会是同一个。如果不满足这种幂等性，将可能导致不一致的问题。

因此，我们可以把 Paxos 的基本命题提炼出来：

P1. 在一次 Paxos 流程中，如果一个值（Value）为 v 的提案（Proposal）被选定（Chosen）了，那么后续任何被最终选定的带有更大编号（Number）的提案中的 Value 也必须是 v。

提案在被最终选定之前必须先被 Acceptor 接受，于是我们可以再进一步总结一个具有更强约束的命题：

P2. 在一次 Paxos 流程中，如果一个值（Value）为 v 的提案（Proposal）被选定（Chosen）了，那么后续任何被 Acceptor 接受的带有更大编号（Number）的提案中的 Value 也必须是 v。

这还不是具备最强约束的命题，因为提案在被 Acceptor 接受之前必须先由 Proposer 提出，因此还可以继续强化命题：

P3. 在一次 Paxos 流程中，如果一个值（Value）为 v 的提案（Proposal）被选定（Chosen）了，那么后续任何 Proposer 提议的带有更大编号（Number）的提案中的 Value 也必须是 v。

从上述的三个命题，我们可以很容易地看出来，P3 可以推导出 P2，进而推导出 P1，也就是说这是一个归约的过程，因此只要 P3 成立则 P1 成立，也就是 Paxos 算法的正确性得到保证。

那么要如何实现呢 P3 呢？只需满足如下约束：

C3. 对于一个被 Proposer 提议的提案中任意的 v 和 n，存在一个数量超过半数 Acceptors 的集合 S，满足以下两个条件中的任意一个：

• S 中的任何一个 Acceptor 都没有接受过编号小于 n 的提案。

• S 中所有的 Acceptors 接受过的最大编号的提案的 Value 为 v。

为了满足 C3 从而实现 P3，需要引入一条约束：Proposer 每次生成自己的 n 之后，发起提案之前，必须要先去『学习』那个已经被选定或者将要被选定的小于 n 的提案，如果有这个提案的话则把那个提案的 v 作为自己的此次提案的 Value，没有的话才可以自己指定一个 Value，这样的话 Proposer 侧就可以保证更高编号的提案的值只会是已选定的 v 了，但是 Acceptor 侧还无法保证，因为 Acceptor 有可能还会接受其他的 Proposers 的提案值，于是我们需要对 Acceptor 也加一条约束，让它承诺在收到编号为 n 的 v 之后，不会再接受新的编号小于 n 的提案值。

所以我们可以得到一个 Paxos 在 Proposer 侧的算法流程：

1. Proposer 生成一个新的提案编号 n 然后发送一个 prepare 请求给超过半数的 Acceptors 集合，要求集合中的每一个 Acceptor 做出如下响应：

   (a) 向 Proposer 承诺在收到该消息之后就不再接受编号小于 n 的提案。

   (b) 如果 Acceptor 在收到该消息之前已经接受过其他提案，则把当前接受的编号最大的提案回复给 Proposer。

2. 如果 Proposer 收到了超过半数的 Acceptors 的回复，那么就可以生成 (n, v) 的提案，这里 v 是所有 Acceptors 回复中编号最大的那个提案里的值，如果所有 Acceptors 回复中都没有附带上提案的话，则可以由 Proposer 自己选择一个 v。

3. Proposer 将上面生成的提案通过一个 accept 请求发送给一个超过半数的 Acceptors 集合。（需要注意的是这个集合不一定和第二步中的那个集合是同一个。）

Paxos 在 Proposer 侧的算法流程已经确定了，接下来我们需要从 Acceptor 的视角来完成剩下的算法推导。前面我们提到过，Acceptor 是可以接受多个 Proposers 的多个提案的，但是在收到一个 Proposer 的 prepare 消息后会承诺不再接受编号小于 n 的新提案，也就是说 Acceptor 也是可以忽略掉其他 Proposers 消息（包括 prepare 和 accept）而不会破坏算法的安全性，当然了，在工程实践中也可以直接回复一个错误，让 Proposer 更早知道提案被拒绝然后生成提案重新开始流程。这里我们应该重点思考的场景是一个 Acceptor 接受一个提案请求的时候，根据前面 Proposer 要求 Acceptor 的承诺，我们可以给 Acceptor 设置一个这样的约束：

C4. 如果一个 Proposer 发出了带 n 的 prepare 请求，只要 Acceptor 还没有回复过任何其他编号大于 n 的prepare 请求，则该 Acceptor 可以接受这个提案。

因为 Acceptor 需要对 Proposer 做出不接受编号小于 n 的提案的承诺，因此它需要做持久化记录，那么它就必须是有状态的，也因此每个 Acceptor 都需要利用可靠性存储（日志）来保存两个对象：

1. Acceptor 接受过的编号最大的提案；

2. Acceptor 回复过的最大的 prepare 请求提案编号。

以上这就是 Acceptor 侧的约束。接下来我们就可以得到 Paxos 的整个算法流程了。

Paxos 算法可以归纳为两大基本过程：

1. 选择过程；

2. 学习过程。

选择过程

选择过程分为两个阶段：

• 阶段一（Phase 1）：

  (a) Proposer 生成一个全局唯一且单调递增的提案编号 n，然后发送编号为 n 的 prepare 请求（P1a msg）给超过半数的 Acceptors 集合。

  (b) 当一个 Acceptor 收到一个编号为 n 的 prepare 请求，如果 n 比它此前接受过其他的提案编号（如果有）都要大的话，那么将这个提案编号 n 写入本地日志，这里记为 max_n，然后作出『两个承诺，一个回复』:

  否则就忽略该 prepare 消息或者回复一个错误。

• • 在不违背以前作出的承诺下，回复消息（P1b msg），附带上自己已经接受过的提案中编号最大的那个提案的 v 和 n，没有则返回空值。

  • 不再接受编号小于等于 n 的 prepare 请求

  • 不再接受编号小于等于 n 的 accept 请求

  • 两个承诺：

  • 一个回复：

• 阶段二（Phase 2）：

  (a) 当 Proposer 收到超过半数的 Acceptors 回复它的编号为 n 的 prepare 请求的响应，此时有两种可能：

  (b) 当 Acceptor 收到一个编号为 n 的提案的 accept 请求消息，需要分两种情况处理：

• • 如果 n >= max_n（通常情况下这两个值是相等的），则接受该提案并回复消息（P2b msg）。

  • 如果 n < max_n，则忽略该 accept 消息或者回复一个错误（P2b error）。

  • Free：没有任何一个 Acceptor 的回复消息中附带已被接受的提案，意味着当前流程中还没有提案值被最终接受，此时 Proposer 可以自由地选择提案值 Value，最后发送一个包含 (n, v) 提案的 accept 请求消息（P2a msg）给 Acceptors 集合。

  • Forced：某些 Acceptors 的回复消息中附带已被接受的提案，那么 Proposer 必须强制使用这些回复消息中编号最大的提案 Value 作为自己的提案值，最后发送一个包含 (n, v) 提案的 accept 请求消息（P2a msg）给 Acceptors 集合。

学习过程

选择过程结束之后，我们得到了一个提案值，接下来就是要让集群中的所有 Learner 『学习』到这个值了，以求达到集群的共识。

Learner 学习提案值的方式可以分成三种：

1. 任意一个 Acceptor 接受了一个提案后就立刻将该提案发送给所有 Learner。优点：Learner 能实时学习到被 Paxos 流程选定的 Value；缺点：网络通信次数太多，如果有 N 个 Acceptors 和 M 个 Learner，则需要的网络通信是 N*M 次。

2. 设置一个主 Learner，Acceptor 接受了一个提案后只将该提案发送给主 Learner，主 Learner 再转发给剩下的 Learners。优点：网络通信次数只需 N+M-1 次；缺点：主 Learner 有单点故障的风险。

3. Acceptor 接受了一个提案后将该提案发送给一个 Learner 集合，由这个集合去通知剩下的 Learners。优点：用集合替代单点，可靠性更高；缺点：增加系统复杂度，需要维护一个 Learner 小集群。

至此，我们就推导出了整个 Paxos 算法的流程：

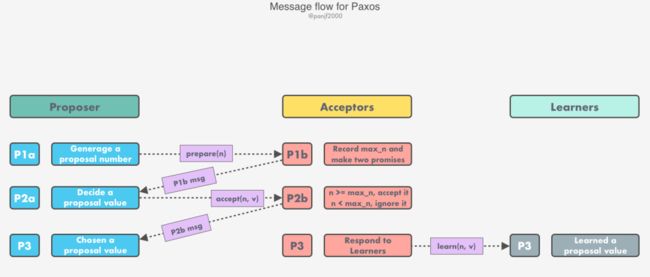
算法证明

这一节我们来证明 Paxos 算法的正确性。

上一节我们已经提炼出来了 Paxos 的基本命题 P1，并通过归约 P1 得到了约束性更强的另外两个命题 P2 和 P3，根据归约的原理，我们知道 P3 可以最终推导出 P1，也就是说如果要证明 Paxos 的基本命题 P1，只需要证明 P3 即可。为什么之前我们要不断强化 Paxos 的命题呢？因为从数学的层面来讲，一个具有更强约束（更多假设）的命题一般会更容易证明。

现在我们把 P1, P2 和 P3 用更严格的数学语言来描述：

P1. 在一次 Paxos 流程中，如果一个包含 (n, v) 的提案被选定（Chosen），那么存在未来被选定的提案 (k, v1)，必然满足 k > n，v1 = v。

P2. 在一次 Paxos 流程中，如果一个包含 (n, v) 的提案被选定（Chosen），那么存在未来被超过半数的 Acceptors 接受的提案 (k, v1)，必然满足 k > n，v1 = v。

P3. 在一次 Paxos 流程中，如果一个包含 (n, v) 的提案被选定（Chosen），那么存在未来由 Proposer 提议的提案 (k, v1)，必然满足 k > n，v1 = v。

现在我们利用数学归纳法来证明 P3：

假设 k = m 时 P3 成立，由于 (n, v) 已经是被选定的提案，因此 Proposer 发起的从 n 到 k 的提案中的 Value 都会是 v，其中 m >= n，那么根据归约的原理可证 k = m 时 P1 也成立。

现在令 k = m+1，Proposer 发送带编号 k 的 prepare 请求消息到 Acceptors 集合。

由于此前已经有了选定的提案，那么根据 Paxos 的约束 C2 可知参与这一个提案投票的 Acceptors 集合必定和上一个集合有重合。

根据 Acceptors 集合重叠和 Paxos 的 P1b 阶段可知，回复的消息中必定附带有已被大多数 Acceptors 接受的提案 (i, v0)。

然后根据 P2a 阶段，Proposer 提案 (k, v1)，其中 v1 = v0。

还是根据 P1b，可知 i 是所有回复消息里编号最大的，可得 i >= m，又根据 P1a 可知 i < k，因此可以得出提案 (i, v0) 中有 v0 = v。

可知当 k = m+1 时，提案 (k, v1) 中的 v1 = v。

根据数学归纳法的原理，我们还需要找到一个特例来使得命题成立，然后由特例推广到普遍，我们这里选择 k = 1 作为特例，证明 k = 1 时 P3 成立：根据 Paxos 的约束 C1 易知在 n = 0，k = 1 的场景下，P3 成立。

因此可根据数学归纳法基于 k = 1 进行推广至 k = m（m 代表任意自然数），最后 P3 命题得证。

再由归约的原理可知，P3 可推导出 P2，最后 P2 推导出 P1。至此， Paxos 算法原理正确性的证明完成。

上述的证明只是一种比较简单且粗浅的证明方法，但是对于工程师理解 Paxos 原理来说已经足够了，如果希望进一步学习 Paxos 原理的严格数学证明，可以参阅 Leslie Lamport 的原始论文《The PartTime Parliament》，里面给出了 Paxos 算法的严格数学证明。

Multi-Paxos

自 Lamport 于 1990 年在论文《The PartTime Parliament》中提出 Paxos 算法之后，这个算法一直被评价为难以理解和实现，这篇论文中运用了大量的数学对 Paxos 的原理进行证明，而又由于 Lamport 在论文里用讲故事的形式解释 Paxos，进一步增大了人们彻底理解 Paxos 的难度，事实上 Lamport 的这篇论文也因此在发表过程中一波三折，这里不展开，有兴趣的读者可以自行去了解这段这段背景故事。

因为业界在理解 Paxos 算法上持续的怨声载道，Lamport 在 2001 年发表了论文《Paxos Made Simple》，对原论文进行精简，以更通俗易懂的语言和形式阐述 Paxos 算法，并在其中提出了更加具备工程实践性的 Multi-Paxos 的思想。

关于 Paxos 难以理解的问题上，我个人的一点愚见是：Paxos 算法的思想其实并不难理解，真正难的地方是：

1. Paxos 背后那一套完整的数学原理和证明

2. 在复杂分布式环境将 Paxos 进行工程落地

我个人建议的 Paxos 学习资料是：《Paxos Made Simple》，《Paxos Made Live - An Engineering Perspective》以及 Paxos lecture (Raft user study)。第一篇论文可以说是 Lamport  1990 年那篇最初的论文的精简版，可读性提高了很多，论文里也没有使用任何数学公式，只需一点英文基础就可以通读，第二篇论文讲的则是 Google 内部基于 Multi-Paxos 实现的分布式锁机制和小文件存储系统，这是业界较早的实现了 Multi-Paxos 的大规模线上系统，十分具有参考性，最后的 Youtube 视频则是 Raft 的作者 Diego Ongaro 为了对比 Raft 和 Multi-Paxos 的学习的难易程度而做的，非常适合作为学习 Paxos 和 Raft 的入门资料。

从上一节可知 Basic Paxos 算法有几个天然缺陷：

• 只能就单个值（Value）达成共识，不支持多值共识。在实际的工程实践中往往是需要对一系列的操作达成共识，比如分布式事务，由很多执行命令组成。

• 至少需要 2 轮往返 4 次 prepare 和 accept 网络通信才能基于一项提案达成共识。对于一个分布式系统来说，网络通信是最影响性能的因素之一，过多的网络通信往往会导致系统的性能瓶颈。

• 不限制 Proposer 数量导致非常容易发生提案冲突。极端情况下，多 Proposer 会导致系统出现『活锁』，破坏分布式共识算法的两大约束之一的活性（liveness）。

关于第三点，前文提到分布式共识算法必须满足两个最核心的约束：安全性（safety）和活性（liveness），从上一节我们可以看出 Basic Paxos 主要着重于 safety，而对 liveness 并没有进行强约束，让我们设想一种场景：两个 Proposers (记为 P1 和 P2) 轮替着发起提案，导致两个 Paxos 流程重叠了：

1. 首先，P1 发送编号 N1 的 prepare 请求到 Acceptors 集合，收到了过半的回复，完成阶段一。

2. 紧接着 P2 也进入阶段一，发送编号 N2 的 prepare 请求到过半的 Acceptors 集合，也收到了过半的回复，Acceptors 集合承诺不再接受编号小于 N2 的提案。

3. 然后 P1 进入阶段二，发送编号 N1 的 accept 请求被 Acceptors 忽略，于是 P1 重新进入阶段一发送编号 N3 的 prepare 请求到 Acceptors 集合，Acceptors 又承诺不再接受编号小于 N3 的提案。

4. 紧接着 P2 进入阶段二，发送编号 N2 的 accept 请求，又被 Acceptors 忽略。

5. 不断重复上面的过程......

在极端情况下，这个过程会永远持续，导致所谓的『活锁』，永远无法选定一个提案，也就是 liveness 约束无法满足。

为了解决这些问题，Lamport 在《Paxos Made Simple》论文中提出了一种基于 Basic Paxos 的 Multi-Paxos 算法思想，并基于该算法引出了一个分布式银行系统状态机的实现方案，感兴趣的读者不妨看一下。

Multi-Paxos 算法在 Basic Paxos 的基础上做了两点改进：

1. 多 Paxos 实例：针对每一个需要达成共识的单值都运行一次 Basic Paxos 算法的实例，并使用 Instance ID 做标识，最后汇总完成多值共识。

2. 选举单一的 Leader Proposer：选举出一个 Leader Proposer，所有提案只能由 Leader Proposer 来发起并决策，Leader Proposer 作为 Paxos 算法流程中唯一的提案发起者，『活锁』将不复存在。此外，由于单一 Proposer 不存在提案竞争的问题，Paxos 算法流程中的阶段一中的 prepare 步骤也可以省略掉，从而将两阶段流程变成一阶段，大大减少网络通信次数。

关于多值共识的优化，如果每一个 Basic Paxos 算法实例都设置一个 Leader Proposer 来工作，还是会产生大量的网络通信开销，因此，多个 Paxos 实例可以共享同一个 Leader Proposer，这要求该 Leader Proposer 必须是稳定的，也即 Leader 不应该在 Paxos 流程中崩溃或改变。

由于 Lamport 在论文中提出的 Multi-Paxos 只是一种思想而非一个具体算法，因此关于 Multi-Paxos 的很多细节他并没有给出具体的实现方案，有些即便给出了方案也描述得不是很清楚，比如他在论文中最后一节提出的基于银行系统的状态机中的多 Paxos 实例处理，虽然给了具体的论述，但是在很多关键地方还是没有指明，这也导致了后续业界里的 Multi-Paxos 实现各不相同。

我们这里用 Google Chubby 的 Multi-Paxos 实现来分析这个算法。

首先，Chubby 通过引入 Master 节点，实现了 Lamport 在论文中提到的 single distinguished proposer，也就是 Leader Proposer，Leader Proposer 作为 Paxos 算法流程中唯一的提案发起者，规避了多 Proposers 同时发起提案的场景，也就不存在提案冲突的情况了，从而解决了『活锁』的问题，保证了算法的活性（liveness）。

Lamport 在论文中指出，选择 Leader Proposer 的过程必须是可靠的，那么具体如何选择一个 Leader Proposer 呢？在 Chubby 中，集群利用 Basic Paxos 算法的共识功能来完成对 Leader Proposer 的选举，这个实现是具有天然合理性的，因为 Basic Paxos 本身就是一个非常可靠而且经过严格数学证明的共识算法，用来作为选举算法再合适不过了，在 Multi-Paxos 流程期间，Master 会通过不断续租的方式来延长租期（Lease）。比如在实际场景中，一般在长达几天的时期内都是同一个服务器节点作为 Master。万一 Master 故障了，那么剩下的 Slaves 节点会重新发起 Paxos 流程票选出新的 Master，也就是说主节点是一直存在的，而且是唯一的。

此外，Lamport 在论文中提到的过一种优化网络通信的方法：“当 Leader Proposer 处于稳定状态时，可以跳过阶段一，直接进入阶段二”，在 Chubby 中也实现了这个优化机制，Leader  Proposer 在为多个 Paxos 算法实例服务的时候直接跳过阶段一进入阶段二，只发送 accept 请求消息给 Acceptors 集合，将算法从两阶段优化成了一阶段，大大节省网络带宽和提升系统性能。

最后，Multi-Paxos 是一个"脑裂"容错的算法思想，就是说当 Multi-Paxos 流程中因为网络问题而出现多 Leaders 的情况下，该算法的安全性（safety ）约束依然能得到保证，因为在这种情况下，Multi-Paxos 实际上是退化成了 Basic Paxos，而 Basic Paxos 天然就支持多 Proposers。

在分布式事务中，Paxos 算法能够提供比两阶段提交协议更加可靠的一致性提交：通过将提交/放弃事务的决定从原来两阶段协议中单一的协调者转移到一个由 Proposer + Acceptors 组成的集群中。Lamport 曾经发表过一篇《Consensus on Transaction Commit》的论文，通过将两阶段提交协议和基于 Paxos 实现的分布式提交协议做对比，对基于 Paxos 实现的提交协议有非常精彩的论述，感兴趣的读者不妨一读。

Raft

Raft 算法实际上是 Multi-Paxos 的一个变种，通过新增两个约束：

1. 追加日志约束：Raft 中追加节点的日志必须是串行连续的，而 Multi-Paxos 中则可以并发追加日志（实际上 Multi-Paxos 的并发也只是针对日志追加，最后应用到内部 State Machine 的时候还是必须保证顺序）。

2. 选主限制：Raft 中只有那些拥有最新、最全日志的节点才能当选 Leader 节点，而 Multi-Paxos 由于允许并发写日志，因此无法确定一个拥有最新、最全日志的节点，因此可以选择任意一个节点作为 Leader，但是选主之后必须要把 Leader 节点的日志补全。

基于这两个限制，Raft 算法的实现比 Multi-Paxos 更加简单易懂，不过由于 Multi-Paxos 的并发度更高，因此从理论上来说 Multi-Paxos 的性能会更好一些，但是到现在为止业界也没有一份权威的测试报告来支撑这一观点。

对比一下 Multi-Paxos 和 Raft 下集群中可能存在的日志顺序：

可以看出，Raft 中永远满足这样一个约束：follower log 一定会是 leader log 的子集并且顺序一定是连续的，而 Multi-Paxos 则不一定满足这个约束，日志记录通常是乱序的。

由于 Raft 的核心思想源自 Multi-Paxos，在实现过程中做了很多改进优化，然而万变不离其宗，我相信理解了 Multi-Paxos 之后再去学习 Raft 会事半功倍（Raft 在诞生之初也是打着"容易理解"的旗号来对标 Paxos 的），由于前面已经深度剖析过 Paxos 算法的流程和原理了，碍于本文的篇幅所限，这里就不再对 Raft 算法的细节进行深入探讨了，如果有意深入学习 Raft，可以从 The Raft Consensus Algorithm 处找到相关的论文、源码等资料进行全面的学习。

最后有一些概念要澄清一下，Basic Paxos 是一个经过了严格数学证明的分布式共识算法，但是由于前文提到的 Basic Paxos 算法应用在实际工程落地中的种种问题，现实中几乎没有直接基于 Basic Paxos 算法实现的分布式系统，绝大多数都是基于 Multi-Paxos，然而 Multi-Basic 仅仅是一种对 Basic Paxos 的延伸思想而非一个具体算法，问题在于目前业界并没有一个统一的 Multi-Paxos 实现标准，因此 Multi-Paxos 的工程实现是建立在一个未经严格证明的前提之上的，工程实现最终的正确性只能靠实现方自己去验证，而 Raft 则是一个具有统一标准实现的、正确性已经过严格证明的具体算法，因此在分布式系统的工程实践中大多数人往往还是会选择 Raft 作为底层的共识算法。

算法类型

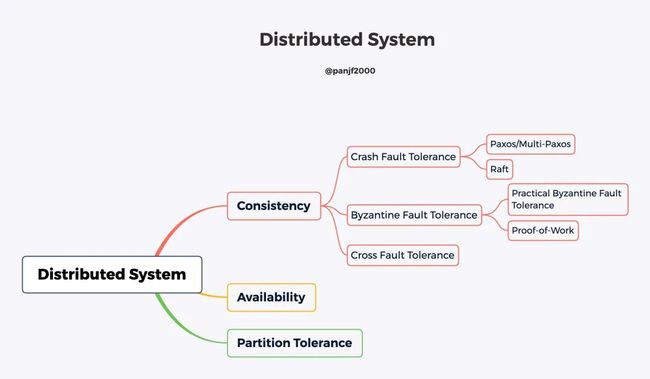
需要特别指出的一点是，根据解决的场景是否允许拜占庭（Byzantine）错误，共识算法可以分为 Crash Fault Tolerance (CFT) 和 Byzantine Fault Tolerance（BFT）两类。

对于非拜占庭错误的情况，已经存在不少经典的算法，包括 Paxos（1990 年）、Raft（2014 年）及其变种等。这类容错算法往往性能比较好，处理较快，容忍不超过一半的故障节点。

对于要能容忍拜占庭错误的情况，包括 PBFT（Practical Byzantine Fault Tolerance，1999 年）为代表的确定性系列算法、PoW（1997 年）为代表的概率算法等。确定性算法一旦达成共识就不可逆转，即共识是最终结果；而概率类算法的共识结果则是临时的，随着时间推移或某种强化，共识结果被推翻的概率越来越小，最终成为事实上结果。拜占庭类容错算法往往性能较差，容忍不超过 1/3 的故障节点。

本文主要讨论的分布式共识算法是 CFT 类算法，毕竟对于大多数分布式系统来说，集群节点和网络消息一般都是可控的，系统只会出现节点故障而不会出现像拜占庭错误那样伪造的、欺骗性的网络消息，在这种场景下，CFT 类算法更具有现实意义；BFT/PBFT 类算法更多是用在系统被恶意入侵，故意伪造网络消息的场景里。

并发控制

在分布式事务中，集群中的每个服务器节点要管理很多资源对象，每个节点必须保证在并发事务访问这些资源对象时，它们能够始终保持一致性。因此，每个服务器节点需要对自己的管理的资源对象应用一定的并发控制机制。分布式事务中需要所有服务器节点共同保证事务以串行等价的的方式执行。

也就是说，如果事务 T 对某一个服务器节点上的资源对象 S 的并发访问在事务 U 之前，那么我们需要保证在所有服务器节点上对 S 和其他资源对象的冲突访问，T 始终在 U 之前。

锁并发控制

在分布式事务中，某个对象的锁总是本地持有的（在同一个服务器节点上）。是否加锁是由本地锁管理器（Local Lock Manager，LLM）决定的。LLM 决定是满足客户端持锁的请求，还是阻塞客户端发起的分布式事务。但是，事务在所有服务器节点上被提交或者放弃之前，LLM 不能释放任何锁。在使用加锁机制的并发控制中，原子提交协议在进行的过程中资源对象始终被锁住，并且是排他锁，其他事务无法染指这些资源对象。但如果事务在两阶段提交协议的阶段一就被放弃，则互斥锁可以提前释放。

由于不同服务器节点上的 LLM 独立设置资源对象锁，因此，对于不同的事务，它们加锁的顺序也可能出现不一致。考虑一个场景：事务 T 和 U在服务器 X 和 Y 之间的交错执行：

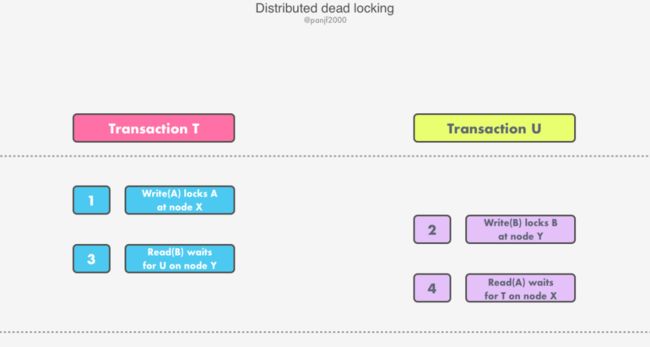
1. 事务 T 锁住了服务器节点 X 上的资源对象 A，做写入操作；

2. 事务 U 锁住了服务器节点 Y 上的资源对象 B，做写入操作；

3. 事务 T 试图读取服务器节点 Y 上的资源对象 B，此时 B 被事务 U 锁住，因此 T 等待锁释放；

4. 事务 U 试图读取服务器节点 X 上的资源对象 A，此时 A 被事务 T 锁住，因此 U 等待锁释放。

在服务器节点 X 上，事务 T 在事务 U 之前；而在服务器节点 Y 上，事务 U 在事务 T 之前。这种不一致的事务次序导致了事务之间的循环依赖，从而引起分布式死锁。分布式死锁需要通过特定的方法/算法来检测并解除，一旦检测到死锁，则必须放弃其中的某个事务来解除死锁，然后通知事务协调者，它将会放弃该事务所涉及的所有参与者上的事务。

时间戳并发控制

对于单一服务器节点的事务来说，协调者在每个事务启动时会为其分配一个全局唯一的时间戳。通过按照访问资源对象的事务时间戳顺序提交资源对象的版本来强制保证以事务执行的串行等价性。在分布式事务中，协调者必须保证每个事务都会附带全局唯一的时间戳。全局唯一的时间戳由事务访问的第一个协调者发给客户端。如果任意一个服务器节点上的资源对象执行了事务中的一个操作，那么事务时间戳会被发送给该服务器节点上的协调者。

分布式事务中的所有服务器节点共同保证事务以串行等价的方式执行。例如，如果在某服务器节点上，由事务 U 访问的资源对象版本在事务 T 访问之后提交；而在另一个服务器节点上，事务 T 和事务 U 又访问了同一个资源对象，那么它们也必须按照相同的次序提交资源对象。为了保证所有服务器节点上的事务执行的相同顺序，协调者必须就时间戳排序达成一致。时间戳是一个二元组 < 本地时间戳，服务器 ID > 对。在时间戳的比较排序过程中，首先比较本地时间戳，然后再比较服务器 ID。

一个可靠的时间戳并发控制应该保证即使各个服务器节点之间的本地时间不同步，也能保证事务之间的相同顺序。但是考虑到效率，各个协调者之间的时间戳还是最好还是要求大致同步。这样的话，事务之间的顺序通常与它们实际开始的时间顺序相一致。可以利用一些本地物理时钟同步方法来保证时间戳的大致同步。

如果决定利用时间戳机制进行分布式事务的并发控制，那么还需要通过某些方法来解决事务冲突问题。如果为了解决冲突需要放弃某个事务时，相应的协调者会收到通知，并且它将在所有的参与者上放弃该事务。这样，如果事务能够坚持到客户端发起提交请求命令的那个时候，那么这个事务就总能被提交。因此在两阶段提交协议中，正常情况下参与者都会同意提交，唯一一种不同意提交的情况是参与者在事务执行过程中曾经崩溃过。

乐观并发控制

加锁机制这一类悲观并发控制有许多明显的缺陷：

• 锁的维护带来了很多新的开销。这些开销在不支持对共享数据并发访问的系统中是不存在的。即使是只读事务（如查询），就算这一类事务不会改变数据的完整性，却仍然需要利用锁来保证数据在读取过程中不会被其他事务修改，然而锁却只在最极端的情况下才会发挥作用。

• 锁机制非常容易引发死锁。预防死锁会严重降低并发度，因此必须利用超时或者死锁检测来解除死锁，但这些死锁解除方案对于交互式的程序来说并不是很理想。

• 锁周期过长。为了避免事务的连锁（雪崩）放弃，锁必须保留到事务结束之时才能释放，这再一次严重降低了系统的并发度。

由于锁这一类的悲观并发控制有上述的种种弊端，因此研究者们提出了另一种乐观并发控制的机制，以求规避锁机制的天然缺陷，研究者们发现这样的一个现象：在大多数应用中两个客户端事务访问同一个资源对象的可能性其实很低，事务总是能够成功执行，就好像事务之间不存在冲突一样。

所以事务的乐观并发控制的基本思路就是：各个并发事务只有在执行完成之后并且发出 closeTransaction 请求时，再去检测是否有冲突，如果确实存在冲突，那么就放弃一些事务，然后让客户端重新启动这些事务进行重试。

在乐观并发控制中，每个事务在提交之前都必须进行验证。事务在验证开始时首先要附加一个事务号，事务的串行化就是根据这些事务号的顺序实现的。分布式事务的验证由一组独立的服务器节点共同完成，每个服务器节点验证访问自己资源对象的事务。这些验证在两阶段提交协议的第一个阶段进行。

关于分布式事务的并发控制就暂时介绍到这里，如果想要继续深入学习更多并发控制的细节，可以深入阅读《分布式系统：概念与设计》、《数据库系统实现》和《数据库系统概念》等书籍或者其他资料。

总结

本文通过讲解 BASE 原则、两阶段原子提交协议、三阶段原子提交协议、Paxos/Multi-Paxos 分布式共识算法的原理与证明、Raft 分布式共识算法和分布式事务的并发控制等内容，为读者全面而又深入地讲解分析了分布式事务/系统的底层核心原理，特别是通过对原子提交协议中的 2PC/3PC 的阐述和分析，以及对分布式共识算法 Paxos 的原理剖析和正确性的证明，最后还有对分布式事务中几种并发控制的介绍，相信能够让读者对分布式事务/系统底层的一致性和并发控制原理有一个深刻的认知，对以后学习和理解分布式系统大有裨益。

本文不仅仅是简单地介绍分布式事务和分布式系统的底层原理，更是在介绍原理的同时，通过层层递进的方式引导读者去真正地理解分布式系统的底层原理和设计思路，而非让读者死记硬背一些概念，所以希望通过这篇抛砖引玉的文章，能够对本文读者在以后学习、操作甚至是设计分布式系统以及分布式事务时的思路有所开拓。

参考&延伸

• ACID

• Eventual consistency

• Atomic commit

• A Two-Phase Commit Protocol and its Performance

• The PartTime Parliament

• Paxos Made Simple

• Fast Paxos

• The Performance of Paxos and Fast Paxos

• Paxos Made Live - An Engineering Perspective

• Paxos (computer science)

• The Chubby lock service for loosely-coupled distributed systems

• Consensus on Transaction Commit

• Life beyond Distributed Transactions: an Apostate’s Opinion

• In Search of an Understandable Consensus Algorithm

• Paxos lecture (Raft user study)

• Distributed Systems: Concepts and Design

• How to Build a Highly Available System Using Consensus

• 数学归纳法

• 共识算法

• Distributed Transaction Processing: The XA Specification

References

[1] DTP Model: http://pubs.opengroup.org/onlinepubs/009680699/toc.pdf
[2] 《The PartTime Parliament》: https://lamport.azurewebsites.net/pubs/lamport-paxos.pdf
[3] 《Paxos Made Simple》: https://lamport.azurewebsites.net/pubs/paxos-simple.pdf
[4] 归约: https://zh.wikipedia.org/wiki/%E6%AD%B8%E7%B4%84
[5] 《The PartTime Parliament》: https://lamport.azurewebsites.net/pubs/lamport-paxos.pdf
[6] 《The PartTime Parliament》: https://lamport.azurewebsites.net/pubs/lamport-paxos.pdf
[7] 《Paxos Made Simple》: https://lamport.azurewebsites.net/pubs/paxos-simple.pdf
[8] 《Paxos Made Simple》: https://lamport.azurewebsites.net/pubs/paxos-simple.pdf
[9] 《Paxos Made Live - An Engineering Perspective》: https://read.seas.harvard.edu/~kohler/class/08w-dsi/chandra07paxos.pdf
[10] Paxos lecture (Raft user study): https://www.youtube.com/watch?v=JEpsBg0AO6o
[11] 《Paxos Made Simple》: https://lamport.azurewebsites.net/pubs/paxos-simple.pdf
[12] 《Consensus on Transaction Commit》: https://lamport.azurewebsites.net/video/consensus-on-transaction-commit.pdf
[13] The Raft Consensus Algorithm: https://raft.github.io
[14] ACID: https://en.wikipedia.org/wiki/ACID
[15] Eventual consistency: https://en.wikipedia.org/wiki/Eventual_consistency
[16] Atomic commit: https://en.wikipedia.org/wiki/Atomic_commit
[17] A Two-Phase Commit Protocol and its Performance : https://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=558282
[18] The PartTime Parliament: https://lamport.azurewebsites.net/pubs/lamport-paxos.pdf
[19] Paxos Made Simple: https://lamport.azurewebsites.net/pubs/paxos-simple.pdf
[20] Fast Paxos: https://www.microsoft.com/en-us/research/wp-content/uploads/2016/02/tr-2005-112.pdf
[21] The Performance of Paxos and Fast Paxos: https://arxiv.org/pdf/1308.1358.pdf
[22] Paxos Made Live - An Engineering Perspective: https://read.seas.harvard.edu/~kohler/class/08w-dsi/chandra07paxos.pdf
[23] Paxos (computer science): https://en.wikipedia.org/wiki/Paxos_(computer_science)
[24] The Chubby lock service for loosely-coupled distributed systems: https://static.googleusercontent.com/media/research.google.com/zh-CN//archive/chubby-osdi06.pdf
[25] Consensus on Transaction Commit: https://lamport.azurewebsites.net/video/consensus-on-transaction-commit.pdf
[26] Life beyond Distributed Transactions: an Apostate’s Opinion: https://www.ics.uci.edu/~cs223/papers/cidr07p15.pdf
[27] In Search of an Understandable Consensus Algorithm: https://raft.github.io/raft.pdf
[28] Paxos lecture (Raft user study): https://www.youtube.com/watch?v=JEpsBg0AO6o
[29] Distributed Systems: Concepts and Design: https://ce.guilan.ac.ir/images/other/soft/distribdystems.pdf
[30] How to Build a Highly Available System Using Consensus: https://www.microsoft.com/en-us/research/uploads/prod/1996/10/Acrobat-58-Copy.pdf
[31] 数学归纳法: https://zh.wikipedia.org/wiki/%E6%95%B0%E5%AD%A6%E5%BD%92%E7%BA%B3%E6%B3%95
[32] 共识算法: https://yeasy.gitbook.io/blockchain_guide/04_distributed_system/algorithms
[33] Distributed Transaction Processing: The XA Specification: https://pubs.opengroup.org/onlinepubs/009680699/toc.pdf

- END -

---

看完一键三连在看，转发，点赞

是对文章最大的赞赏，极客重生感谢你

推荐阅读

C语言登顶！|2021年7月编程语言排行榜

深入理解 MySQL 索引底层原理

JVM底层原理解析

觉得内容还不错的话，给我点个 “在看” 呗！