线段树原理及总结

 

一、概述

  线段树是一种在线算法，它在各个节点保存一条线段（数组中的一段子数组），主要用于高效解决连续区间的动态查询问题，由于二叉结构的特性，它基本能保持每个操作的复杂度为O(logn)。

二、原理分析及代码实现

   我们从一个经典的例子来了解线段树，问题描如下:从数组arr[0...n-1]中查找某个数组某个区间内的最小值，数组中的元素的值可以随时更新。这使我们非常困扰，因为当数组非常大的时候，就很容易TLE，所以我们亟待一种相对高效的算法，线段树应运而生。

1，建树。

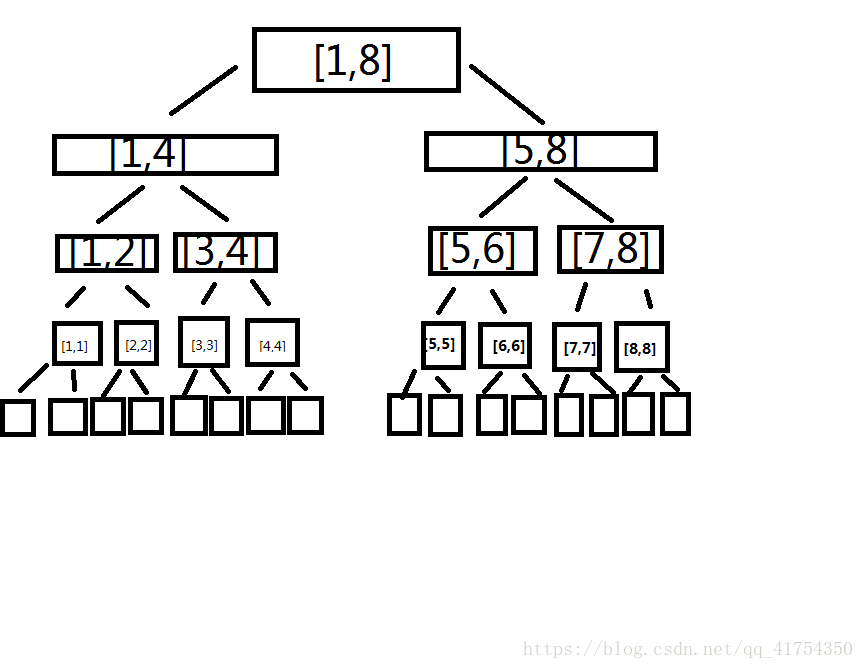
  假如我们要对8个数据进行管理，我们就要建立一个线段树。建立的线段树是一个完全二叉树，我们需要借助一个二叉树的性质：

  父亲的区间是[a,b],(c=(a+b)/2)左儿子的区间是[a,c]，右儿子的区间是[c+1,b]，所以线段树需要的空间为数组大小的四倍。

  函数声明(我们需要根节点，左右两个儿子)，如果到底了，本节点就等于要记载的数组的节点并返回，这也是递归的边界条件，接下来利用性质构筑左右子树mid=(left+right)/2;build(2*root,left,mid);build(2*root+1,mid+1,right)，递归完成后，父节点更新。
 

 

2、单点更新

现在树已经建立完毕，但这还是刚刚开始的存图环节，假如说现在我们要使一个节点更新，比如让第三个数所对应的arr【3】+5，会产生“牵一发而动全身”的效应，所以们们需要对它上面的节点再次更新。

假如arr【1-8】为 1,8,7,3,9,2,4,6 如图所示：

我们要对数组3加上一个5，要达到以下结果。

  我们需要对每一个节点更新，使用的数据有本次的根节点，要控制的总范围区间（左，右），要修改的点和要修改的数据。持续更新它的父节点直到顶端即可。

3，区间更新

  区间更新是个大问题，很多同学会想到用一个for循环，每个点走一遍。虽说思维难度不大，而且在点与点范围跳跃速度也不慢，但当要修改的数据到达一定规模时，这样重复的操作显得累赘而消耗巨量时间，非常容易TLE。所以我们需要找到之间重复的规律，简化程序，以减少不必要的时间浪费。

  于是我们想到了一个方法，引入一个延迟标记。原理是在要修改的区间（有时候是全部，有时候是中间的一部分被完全包括），在不使用它的子孙时，暂且将数据扣留下来，于父亲产生影响，并施加一个延迟标记。有了整个关键方法，我们可以建立一个更新函数，首先先判断它的边界问题，

  举个例子，还是那个图，我们假如说要将arr[2-5]都要加上5，如下图所示，

  我们首先将其与[1,8]进行比较，发现所更改范围在【1,8】之内，我们往下搜索左右子树，发现【1,4】和【5,8】之中都有。先看【1,4】，先搜索它的左子树【1,2】，发现只有2需要，1不需要，所以直接让右子树2所对应的值8+5，返回，返回，至【1,4】。再看右子树【3,4】，发现这全都在更改的范围之内，所以我们在这里加入一个延迟标记并且【3,4】它本身获得它的子树那么多的增加，将扣押下来的值存储在延迟标记，需要的时候再将其放下。然后再看右子树【5,8】，然后引导至【5,6】，【6,6】直接+5就可以了。

  现在我们具体来解释一下延迟标记的原理，提需要接收的信息有本次根节点和左右子树。这是一个更新的例行检查，加入一判定这里有延迟标记，便会产生释放，将数据变动载入真实数组。我们意识到一个严重的问题：假如说产生了多组延迟标记，甚至运算符号不同，这样就会陷入巨大的混乱。说是多次加减，或多次乘除，可直接对延迟标记进行操作。但是假如为加减乘除混合运算，恐怕难以清晰实现，依个人愚见，有两种办法：1、当标记种类较少时，可进行种类判定2、当过于复杂时，不必多种标记分类，不如返璞归真，将上一次标记释放之后在进行新一次的标记。

5、查询

  对于查询问题，是比较容易的一块，他需要接受的信息有，根节点，要实施更新的大环境（左，右），查询的区间（左，右）。首先假如不在就直接返回，假如查询包括了环境范围，就直接利用父节点值，有需要释放的延迟标记就释放，要向下调查左右节点就调查。一切就完毕了。

三、代码的统一展示

第一个是只有加法，第二个是有加法有乘法。

#include
#include
#include
using namespace std;
const long long maxn=900001;
long long arr[maxn];//实际数组
struct node
{
	long long val;//他的节点价值
	long long tag;//延迟标记
}tree[maxn];
long long root,n;
void build(long long root,long long al,long long ar)//建树
{
	tree[root].tag=0;//将延迟标记初始化
	if(al==ar)//如果到底了，就返回
	{
		tree[root].val=arr[al];//储存数组
		return;
	}
	long long mid=(al+ar)/2;
	build(2*root,al,mid);
	build(2*root+1,mid+1,ar);//左右子树的建立
	tree[root].val=tree[2*root].val+tree[2*root+1].val;//递归完毕后再往上更新父节点
}
void pushdown(long long root,long long start,long long end)//延迟标记
{
	if(tree[root].tag!=0)//常规检查，有就释放
	{
		tree[2*root].tag+=tree[root].tag;//左分发下去延迟标记
		tree[2*root+1].tag+=tree[root].tag;//右分发下去延迟标记
		long long mid=(end+start)/2;
        tree[root*2].val+=tree[root].tag*(mid-start+1);//向左下克扣数值
        tree[root*2+1].val+=tree[root].tag*(end-mid);//向右下克扣数值
        tree[root].tag=0;//清除自身标记
	}
}
long long query(long long root,long long al,long long ar,long long ql,long long qr)//查询
{
	if(qrar)//不在范围
	return 0;//直接返回
	if(al>=ql&&ar<=qr)//全在范围
	return tree[root].val;//直接用值
	pushdown(root,al,ar);//如果有延迟标记就清除
	long long mid=(al+ar)/2;
	return query(2*root,al,mid,ql,qr)+query(2*root+1,mid+1,ar,ql,qr);//左右子树查找
}
void update(long long root,long long al,long long ar,long long ul,long long ur,long long addval)//更新节点
{
	if(ul>ar||ur=ul&&ar<=ur)//完全在则直接用延迟标记
	{
		tree[root].val+=addval*(ar-al+1);
		tree[root].tag+=addval;
		return;
	}
	pushdown(root,al,ar);//下放一次
	long long mid=(al+ar)/2;
	update(2*root,al,mid,ul,ur,addval);
	update(2*root+1,mid+1,ar,ul,ur,addval);
	tree[root].val=tree[2*root].val+tree[2*root+1].val;//向上更新
}
int main()
{
	long long m;
	scanf("%lld%lld",&n,&m);
	for(long long i=1;i<=n;++i)
	scanf("%lld",&arr[i]);
	root=1;
	build(1,1,n);
	for(long long i=1;i<=m;++i)
	{
		long long x,ul,ur,addval;
		scanf("%lld",&x);
		if(x==1)//当x==1时，进行修改
		{
			scanf("%lld%lld%lld",&ul,&ur,&addval);
			update(1,1,n,ul,ur,addval);
		}
		if(x==2)//当x==2时，进行查询
		{
			long long e,f;
			scanf("%lld%lld",&e,&f);
			printf("%lld\n",query(1,1,n,e,f));
			
		}
	}
}

#include 
#include 
using namespace std;
//题目中给的p
int p;
//暂存数列的数组
long long a[100007];
//线段树结构体，v表示此时的答案，mul表示乘法意义上的lazytag，add是加法意义上的
struct node{
    long long v, mul, add;
}st[400007];
//buildtree
void bt(int root, int l, int r){
//初始化lazytag
    st[root].mul=1;
    st[root].add=0;
    if(l==r){
        st[root].v=a[l];
    }
    else{
        int m=(l+r)/2;
        bt(root*2, l, m);
        bt(root*2+1, m+1, r);
        st[root].v=st[root*2].v+st[root*2+1].v;
    }
    st[root].v%=p;
    return ;
}
//核心代码，维护lazytag
void pushdown(int root, int l, int r){
    int m=(l+r)/2;
//根据我们规定的优先度，儿子的值=此刻儿子的值*爸爸的乘法lazytag+儿子的区间长度*爸爸的加法lazytag
    st[root*2].v=(st[root*2].v*st[root].mul+st[root].add*(m-l+1))%p;
    st[root*2+1].v=(st[root*2+1].v*st[root].mul+st[root].add*(r-m))%p;
//很好维护的lazytag
    st[root*2].mul=(st[root*2].mul*st[root].mul)%p;
    st[root*2+1].mul=(st[root*2+1].mul*st[root].mul)%p;
    st[root*2].add=(st[root*2].add*st[root].mul+st[root].add)%p;
    st[root*2+1].add=(st[root*2+1].add*st[root].mul+st[root].add)%p;
//把父节点的值初始化
    st[root].mul=1;
    st[root].add=0;
    return ;
}
//update1，乘法，stdl此刻区间的左边，stdr此刻区间的右边，l给出的左边，r给出的右边
void ud1(int root, int stdl, int stdr, int l, int r, long long k){
//假如本区间和给出的区间没有交集
    if(r